父子结构查询_Java面试准备（5）之数据结构与算法——红黑树

欢迎点赞评论+关注~~~~~~~

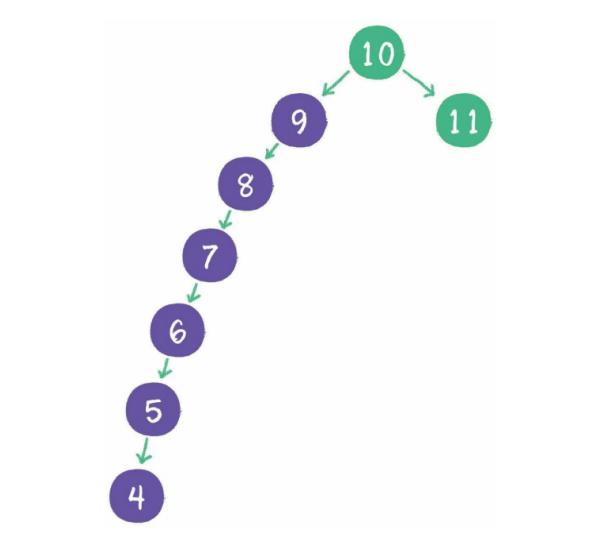
如上图，二叉查找树极端情况下可能会变成一个单链表，这种查询时间复杂度就变成O(n)了，红黑树在二叉查找树的基础上进行了自平衡。

1.原理分析

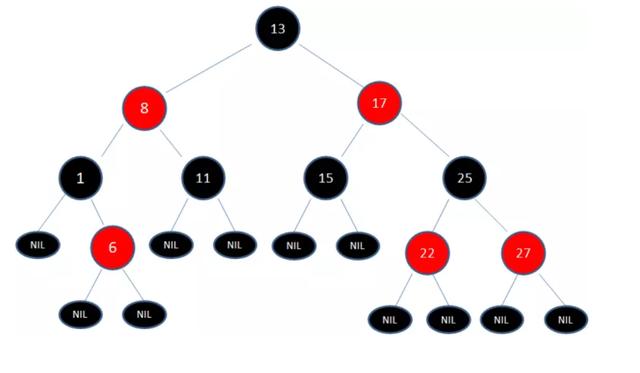
如上图，红黑树具有以下特征：

1. 每个节点要么是黑色，要么是红色

2. 根节点是黑色

3. 每个叶子节点都是黑色的空结点(NIL结点)

4. 如果一个节点是红色的，则它的子节点必须是黑色的

5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点

6.新插入节点默认为红色，插入后需要校验红黑树是否符合规则，不符合则需要进行平衡

红黑树节点的增加删除都需要保证满足以上特征，红黑树采取多种方式来维护这些特征，从而维持平衡。

主要包括：左旋转、右旋转、颜色反转

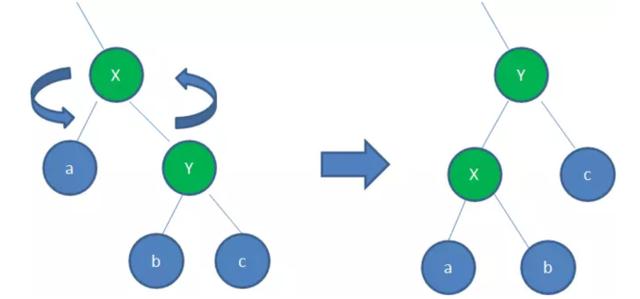
1.1左旋(RotateLeft )

逆时针旋转红黑树的两个结点，使得父结点被自己的右孩子取代，而自己成为自己的左孩子。

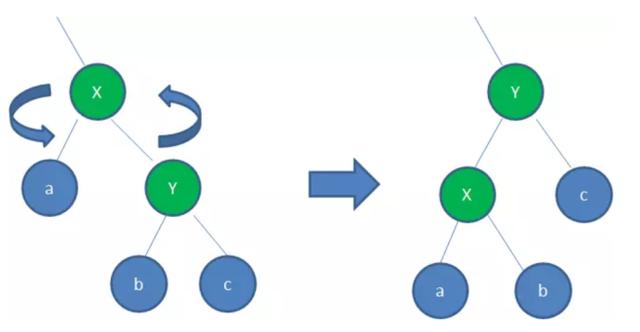
如图所示，以X为基点逆时针旋转，X的父节点被x原来的右孩子Y取代，c保持不变，Y节点原来的左孩子c变成X的右孩子，这样的旋转仍然保证了二叉查找树的特征，左节点比父节点小，右节点仍然比父节点大,即a

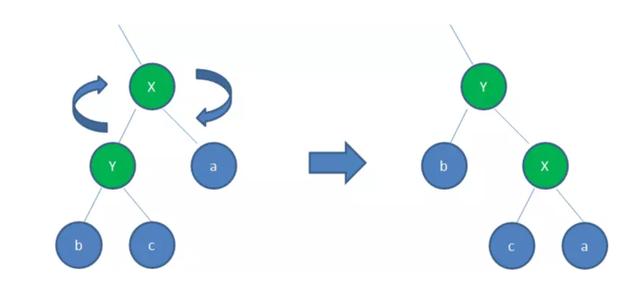
1.2 右旋(RotateRight)

顺时针旋转红黑树的两个结点，使得父结点被自己的左孩子取代，而自己成为自己的右孩子。

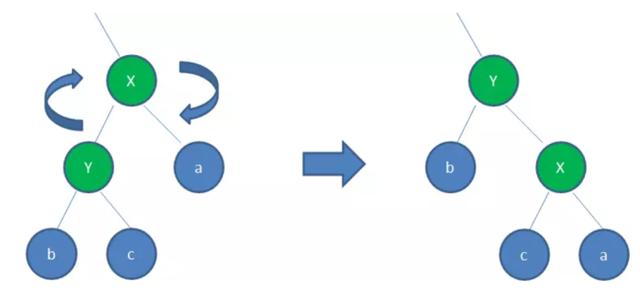
如图所示，以X为基点顺时针旋转，X的父节点被x原来的左孩子Y取代，b保持不变，Y节点原来的右孩子c变成X的左孩子。这样的旋转仍然保证了二叉查找树的特征，左节点比父节点小，右节点仍然比父节点大,即b

1.3颜色反转

新增节点默认为红色，而父节点和叔叔节点也为红色，这种情况就违反了红黑树的规则(父与子不能同时为红色)，需要将红色往祖辈上传，父节点和叔叔节点变为黑色，这样来保证每条叶子结点到根节点的黑色节点数量并未发生变化。

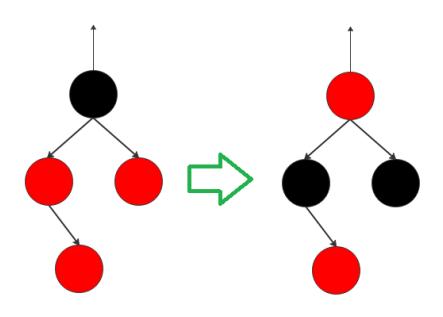
插入新节点的时候存在如下几种情况：

1.插入节点位于树根，没有父节点，这种情况，直接让新结点变色为黑色.

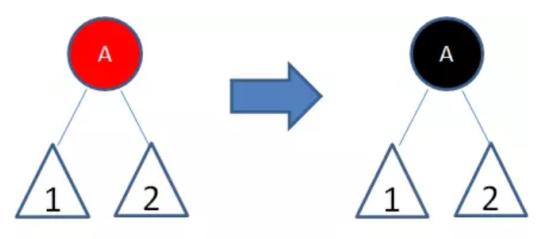
2.插入节点的父节点是黑色,新插入的红色节点并没有打破红黑树的规则，所以不需要做任何调整

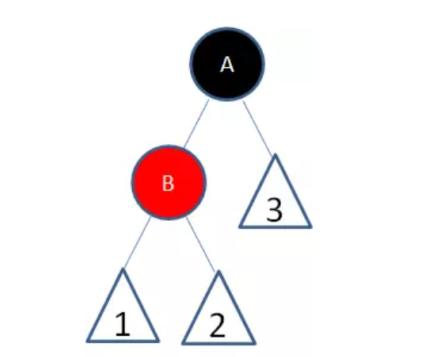
3.插入节点的父节点和叔叔节点是红色

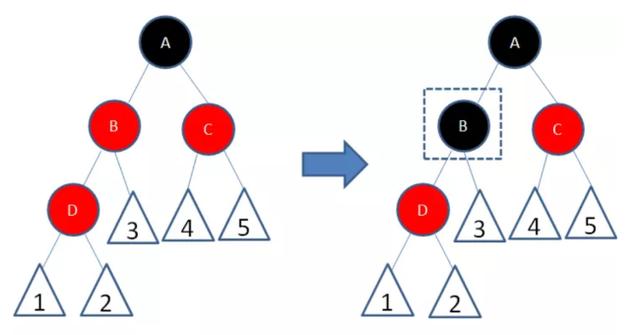
此种情况，不满足父子节点不能同时为红色的规则，先让B变成黑色，这样又不满足某一个节点到每个叶子节点经过的黑色节点数相同的规则，先让A变成红色，

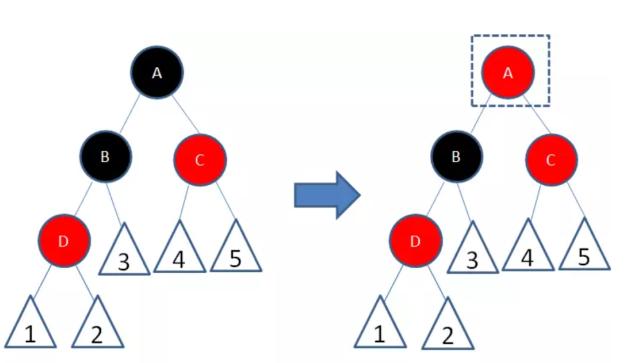
此时，A、C父子节点又变成了红色，所以将C调整为黑色，来使这一局部满足红黑树的规则

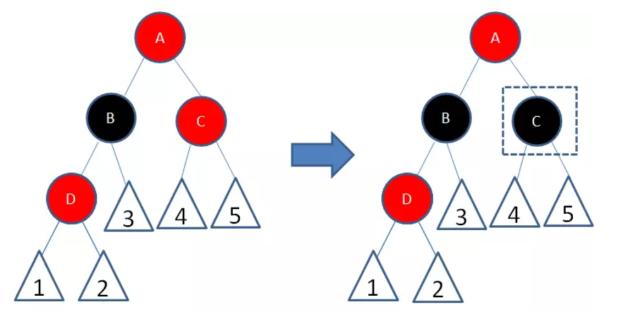
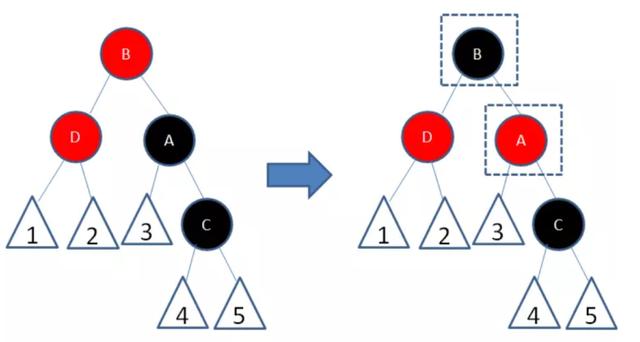
4.插入节点的父节点是红色，叔叔节点是黑色或者没有叔叔，且插入节点是父节点的右孩子，父节点是祖父节点点的左孩子，

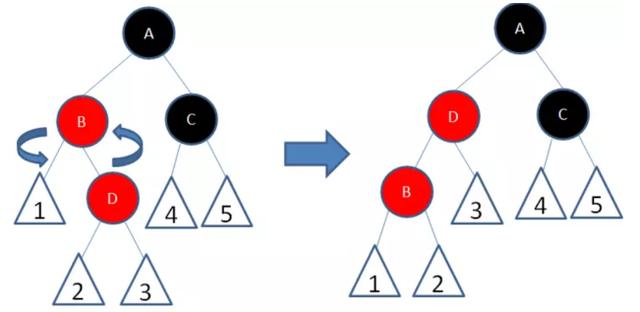
以结点B为轴，做一次左旋转，使得新结点D成为父结点，原来的父结点B成为D的左孩子，变成父节点是红色，叔叔节点是黑色或者没有叔叔，新插入节点是父结点的左孩子，父节点是祖父节点的左孩子，以结点A为轴，做一次右旋转，使得结点B成为祖父结点，结点A成为结点B的右孩子，

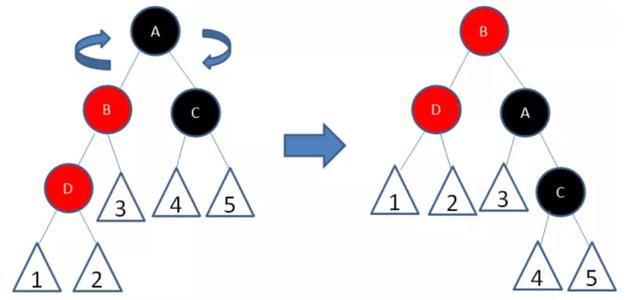
接着，将B变成黑色，A变成红色，就局部满足红黑树的规则了。

小结：旋转和颜色反转都是为了是树满足红黑树的5个特性，从而达到自平衡的效果。

变化规律总结：根节点必黑，新增是红色，只能黑连黑，不能红连红；爸叔通红就变色，爸红叔黑就旋转，哪边黑往哪边转。

2.代码实现

2.1 红黑树节点结构

class RBTreeNode{private int value;//数据    private boolean isBlack;//红黑标记    private RBTreeNode left;//左节点    private RBTreeNode right;//右边节点    private RBTreeNode parent;//父节点    public RBTreeNode(int value) {        this.isBlack=false;//默认节点为红色        this.value = value;    }    setter,getter....}

2.2 遍历节点方法

为了方便获取节点数据，编写一个遍历树的方法,使用递归的方式实现，在树中递归很常用。

public void traverse(RBTreeNode node){        if (node==null) return;        //递归终止条件        if (node.getLeft()==null&& node.getRight()==null){            //叶子节点            System.out.println(node.getValue());            return ;        }        //先遍历左节点,后遍历右节点        traverse(node.getLeft());        traverse(node.getRight());    }

2.3 新增节点

主要是从根节点依次对比 data和node.getValue的大小，一直找到被挂载得节点，在进行挂载。

public void insert(int data){    RBTreeNode node=new RBTreeNode(data);    if (root==null){        //插入根节点        root=node;        root.setBlack(true);//树根是黑色        return;    }    RBTreeNode parent=root;    RBTreeNode son;    if (data

2.4 自平衡方法

自平衡方法按照需求可以拆分为：左旋转、右旋转、设置黑色、设置红色方法

2.4.1 左旋转方法

结合图查看代码逻辑，更清晰旋转过程。

/**     * 左旋转(逆时针旋转)     * @param node     */    private void leftRotate(RBTreeNode node) {        RBTreeNode right = node.getRight();        RBTreeNode parent = node.getParent();        if (parent==null){            //root节点,将            root=right;            right.setParent(null);        }else{            if (parent.getLeft()!=null&&parent.getLeft()==node){ // 左右                //node是左子节点，左旋转直接将node右子节点旋转挂到父节点左节点                parent.setLeft(right);            }else { //右右的情况                //node是子节点，直接将node的右子节点旋转挂到父节点的右子节点                parent.setRight(right);            }            right.setParent(parent);        }        node.setParent(right);        node.setRight(right.getLeft());        if (right.getLeft()!=null){            right.getLeft().setParent(node);        }        right.setLeft(node);    }

2.4.2 右旋转方法

/**     * 右旋转(顺时针)     * @param node     */    private void rightRotate(RBTreeNode node) {        RBTreeNode left = node.getLeft();        RBTreeNode parent = node.getParent();        if (parent == null) {            //根节点            root = left;            left.setParent(null);        } else {            if (parent.getLeft() != null && parent.getLeft() == node) {                //将node的左子节点挂父节点                parent.setLeft(left);            } else {                //将node的左节点挂父节点的右节点                parent.setRight(left);            }            left.setParent(parent);        }        node.setParent(left);        node.setLeft(left.getRight());        if (left.getRight() != null) {            left.getRight().setParent(node);        } left.setRight(node);    }

2.4.3 设置红黑色方法

private void setRed(RBTreeNode node) {        node.setBlack(false);    }    private void setBlack(RBTreeNode node) {        node.setBlack(true);    }

2.4.4 自平衡方法

/**     * 节点自平衡     * @param node     */    private void nodeBanlance(RBTreeNode node) {        RBTreeNode father,gFather;//父节点，祖父节点        //父节点是红色的        while((father=node.getParent())!=null && father.isBlack()==false){            gFather=father.getParent();            if (gFather.getLeft()==father){                //父节点在祖父节点的左侧                RBTreeNode uncle = gFather.getRight();//叔叔节点                if (uncle!=null&& !uncle.isBlack()){                    //叔叔节点不为空 且是红色的                    //这种情况需要反色,父节点和叔叔节点变黑，爷爷节点变红                    setBlack(father);                    setBlack(uncle);                    setRed(gFather);                    //继续循环                    node=gFather;                    continue;                }                if (node==father.getRight()){                    //需要左旋                    leftRotate(father);                    RBTreeNode tmp=node;                    node=father;                    father=tmp;                }                setBlack(father);                setRed(gFather);                //右旋                rightRotate(gFather);            }//父为祖右孩子            else {                RBTreeNode uncle = gFather.getLeft();                if (uncle != null && !uncle.isBlack()) {                    setBlack(father);                    setBlack(uncle);                    setRed(gFather);                    node = gFather;                    continue;                }                if (node == father.getLeft()) {                    //右旋                    rightRotate(father);                    RBTreeNode tmp = node;                    node = father;                    father = tmp;                }                setBlack(father);                setRed(gFather);                //左旋                leftRotate(gFather);            }        }        setBlack(root);    }