python三次样条插值拟合的树行线_数学建模笔记—

啊好像距离上次写作又过了七天，啊好像我之前计划的一周两三篇，啊辣鸡小说毁我青春，啊我是一只可怜的鸽子。

不管怎样，我又回来了，并坚定地更新着hhh。再过两三天就是我们学校数学建模选拔，再过八九天就是期末考试。所以这两天还是一样，写勤快一点儿，之后可能时不时就要断更一周了，八月十九最后一门考完后才能继续安安稳稳地写文章了。没办法，这个暑假实在是不够舒心。

好的，今天我来谈一谈插值和拟合。插值和拟合是两种不同的数值计算方法，分别又有着许多不同的插值算法和拟合算法。在我学习的《数值计算》课中，这两部分好像是讲了三四节课。因为课堂教学的时候，需要对各种算法进行严格的证明和数学推导。

限于篇幅以及个人能力的原因，本文不涉及太多的数学证明与推导(好吧，基本上不推导)。事实上许多经典的建模教材，也不怎么进行推导，主要还是着重于介绍与应用。因此想要对插值和拟合进行深入了解的同学，欢迎自学《数值计算》类课程。

插值

首先谈一谈插值。为什么需要插值呢？因为在许多的实际问题中，我们想要研究一个变量相对于另一个变量的关系，往往只能通过观测得出一组一组的值。而两个变量之间的函数关系，我们往往是难以通过某种解析式或者某种图像来表达的。也就是说，我们只有一组一组的数据，压根不晓得变量之间具体的函数关系。

这就带来了一个难题。举个例子，假设我们观测的是“离海岸距离”与“海水深度”的关系。现在我们将海岸线的位置作为0，每隔50米或者100米测量一次海水的深度，便得到了许多组数据。那现在的问题就是，如果我们想知道距离海岸线326米处的海水深度，怎么求呢？

嗯，最简单的方法就是跑到326米的位置测量一下啦。这确实是最为准确的方法。但是如果有许许多多的点都有待测量，考虑到时间以及其他成本，一个一个测量可能不太现实。因此，我们需要不同的方法来解决这类问题。即已知在之间一些点所对应的值：，我们想要求出节点之间某个位置的函数值。插值就是解决这类问题的一个合适的方法。

插值是什么呢？很简单，插值就是找到一个比较简单的函数，满足，之后使用这个函数来求得之间某个位置的函数值。也就是找一个函数来代替，作为的一个合理近似。

首先举个例子。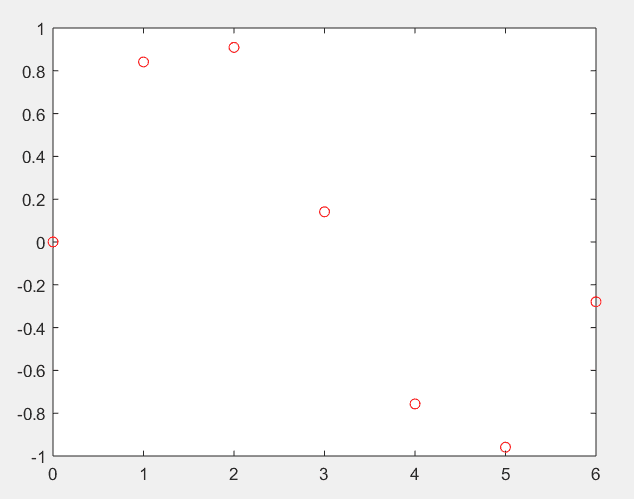

上图是我取出了函数中的7个点。现在假装我们不知道这是个正弦函数，我们只知道这7个点的坐标，那如何求得的函数值呢？求是求不出来的，不知道函数怎么可能求得出来，但我们可以使用插值求一个近似的解。

一种很简单的想法就是分段线性插值，即将相邻的两个点之间用直线进行连接。这种方法应该很容易理解。我们期望用简单的函数来代替，最简单的一种函数应该就是线性函数了吧。嗯，进行一下插值。

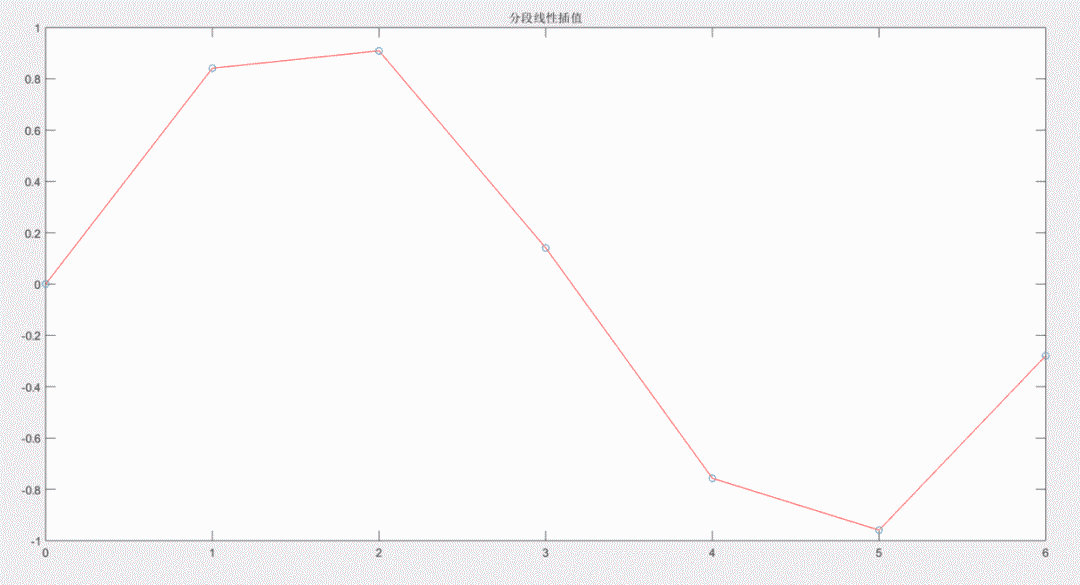
诺，这就是分段线性插值的结果。假如我们现在想要求出时的值，就比较简单。将和这两点之间的直线方程解出来，再把代入，就ok了。

可以看到，上述的插值方法太过简单了，很可能与实际曲线不太相符。在实际问题中，也很少有这种纯线性的的函数关系。因此我们可以使用一些较高阶的多项式进行插值，例如分段三次Hermite插值。直接看看结果。

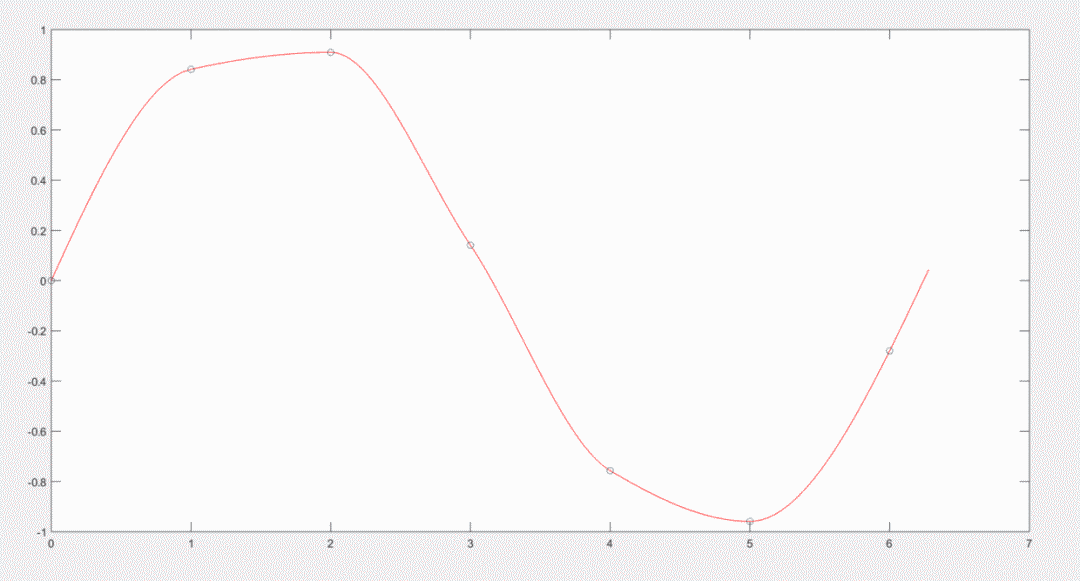
是不是感觉光滑了很多？其实还可以更加光滑一点，我们使用三次样条插值试一试。也是直接放结果。

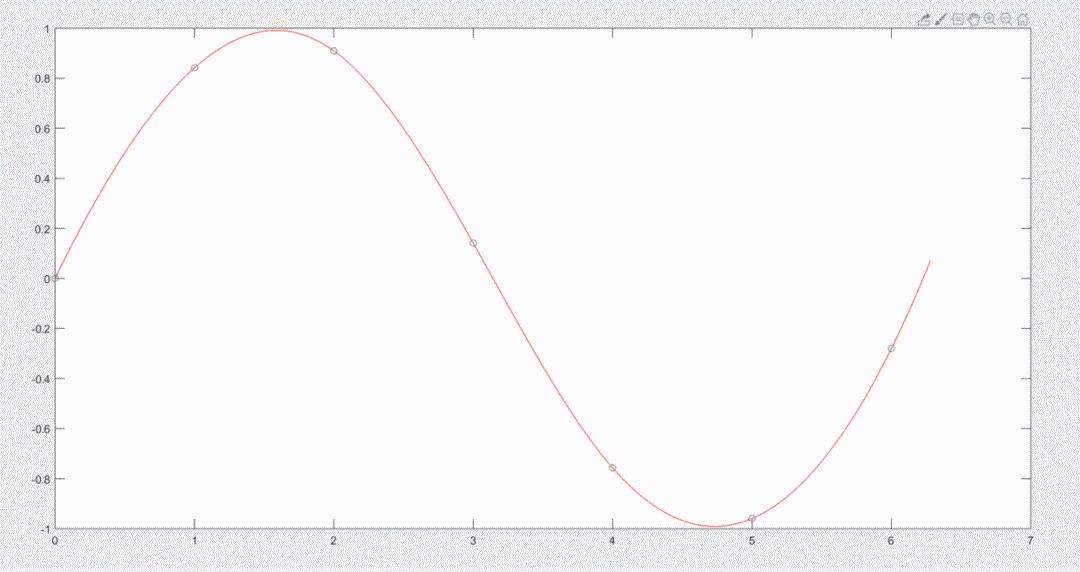
最后我们把上面提到的三种插值以及原函数放在一起看看结果。

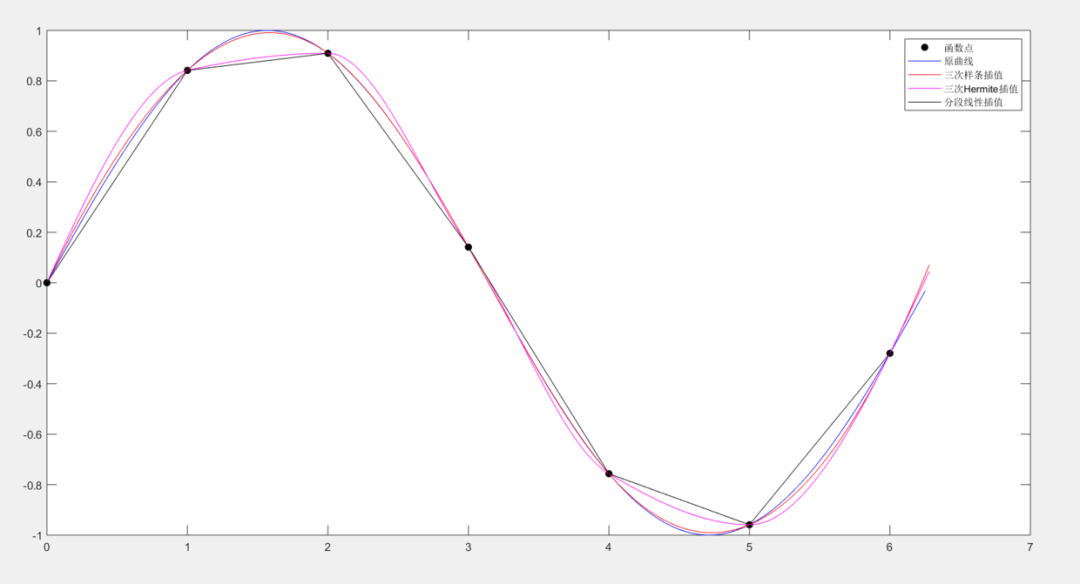
可以看到，三次样条插值最接近原曲线，分段线性插值与原曲线相差最远。这是不是说明三次样条插值一定优于三次Hermite插值与线性插值呢？当然不是，具体的问题还是要具体分析。如果两个变量之间的线性相关性高达99%了，那何必还要进行三次插值呢？不过自然界以及工业界的多种曲线，往往都是较为光滑的，因此我们使用三次样条插值函数较多。

上面只是一个简单的例子，让大家对于插值有一个较为直观的印象。其实很简单，就是找到一个函数，要求该函数曲线必须经过已知点，之后再使用这样一个函数代替原函数，求出某个位置对应的函数值，用这个近似值来代表真实值。接下来简单介绍几种插值算法以及在matlab中的相应函数。

插值的算法还挺多的，例如拉格朗日插值，牛顿插值，最邻近插值等等。不过这里我就介绍比较常用的插值方法，也就是上面提到的分段线性插值，分段三次Hermite插值以及三次样条插值。这三种插值方法有一个共同的特点，即它们是在给定点的每一个小段都确定一个函数表达式，叠加起来作为最终的表达式。嗯，也就是说这是一个分段函数，在之间求一个函数，在求一个函数，依次类推……

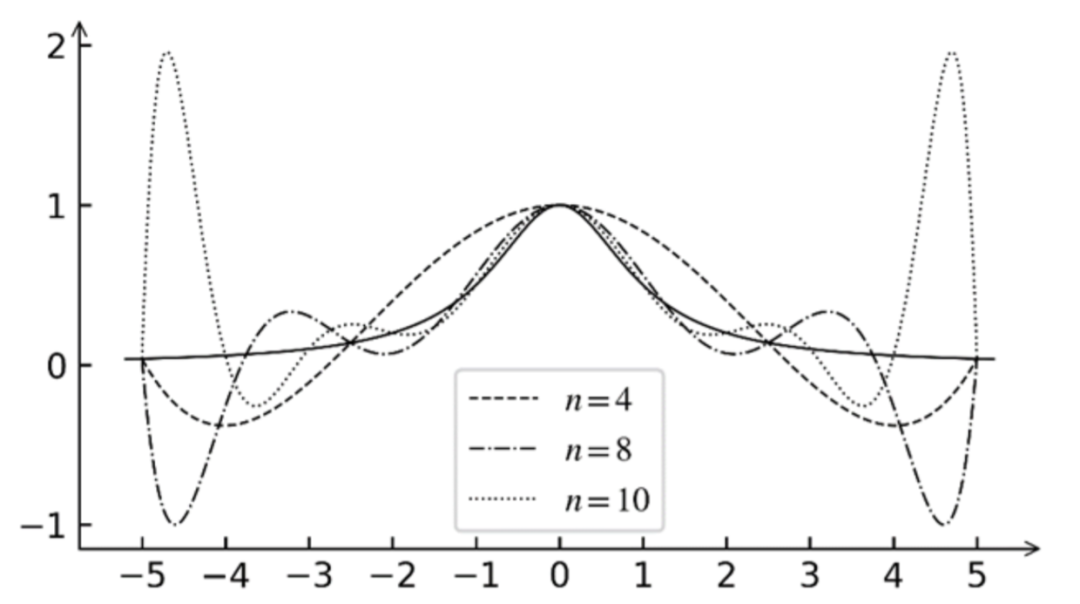
为什么不求出一个单一的函数表达式呢？因为当插值点越多，我们不进行分段时，最终得出来的函数的次数越高，而高次多项式会在插值的区间内发生严重的震荡现象，称之为“龙格现象”。因此我们往往更倾向于使用分段低次多项式来近似原函数。拉格朗日插值以及牛顿插值，最终都是求出一个函数，因此这里不予介绍，有兴趣可以自行了解。嗯，下图是展示龙格现象的一张图。其中黑色实线代表原函数，n代表插值多项式的次数，显而易见，次数越高时，震荡越明显。想要深入了解请自行学习相关内容。

分段线性插值

分段线性插值不必多说了，很简单，就是在相邻的区间内，用直线来近似原函数。用分段线性插值计算点的近似函数值时，只用到左右的两个节点，与其他节点无关。当然啦，越大，分段越多，插值的误差也就越小。实际使用中往往用来计算数学、物理中的特殊函数表，数理统计中的概率分布表等等。在建模过程中，也可以用来进行缺失数据的填补。

matlab中，插值使用到的函数是函数，最后一个是数字不是字母。代表着一维数据。

通过help命令，我们可以看到interp1的使用形式。点击下方“interp1的参考页”，可以进入该函数的帮助文档页面。vq = interp1(x,v,xq,method)中，向量 x 包含样本点，v 包含对应值 v(x)。向量 xq 包含查询点的坐标，vq则返回相应的插值结果。method指定插值方法，如'linear'、'nearest'、'next'、'previous'、 'spline'。默认方法为 'linear'。因此，如果我们想要进行线性插值就很简单，代码如下。

x = 0:2*pi;  %生成[0,2*pi]之间的整数值
y = sin(x);  %生成相应的函数值
plot(x,y,"or");%绘制一下点
xx = 0:0.01:2*pi;%这个是查询点的坐标向量
yy = interp1(x,y,xx,'linear');  %yy就是查询点向量对应的函数值向量了
plot(x,y,"o",xx,yy,"r");%画图画图

xx=1.23;%只查询一个元素也是可以的
yy = interp1(x,y,xx,'linear');%嗯，还是这样
plot(x,y,"o",xx,yy,"or");%画图画图

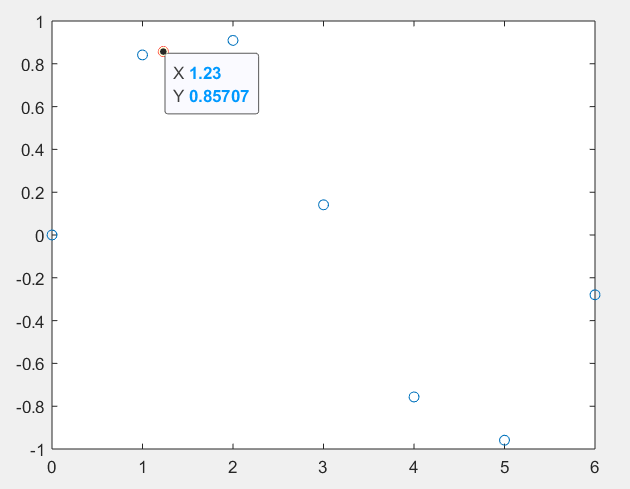
嗯嗯，很简单是吧。对了，线性插值至少需要两个点。我们也可以看到线性插值有一个很明显的缺点，不够光滑。没办法，毕竟是直线。

分段三次Hermite(埃尔米特)插值

分段三次埃尔米特插值比分段线性插值对数据的要求更高一点儿。假设是[a,b]之间的互异节点，且。嗯，也就是我们不仅要知道处对应的函数值，我们也需要知道处对应的函数导数值。

因此我们对相应的插值函数有以下三个要求：

在上一阶可导；
；
在每个上都是三次函数。

满足以上三个条件的插值函数，我们称之为分段三次埃尔米特插值函数。

可以发现，三次埃尔米特插值相较于线性插值有两个特点。一是它不仅要求插值函数过相应的已知点，还要求函数曲线在已知点处一阶导数值等于原函数的导数值，这也是为什么三次埃尔米特在已知点处更为平滑，且与原曲线更为相近。二是它使用三次多项式作为每一个小段的插值多项式，相对于线性函数，三次多项式更为平滑。综上，三次埃尔米特插值相对于线性插值，得到的函数曲线更为平滑且接近原曲线。

matlab之中用于三次埃尔米特插值的函数是，当然也可以使用上面提到的加上参数。

x = 0:2*pi;  %生成[0,2*pi]之间的整数值
y = sin(x);  %生成相应的函数值
plot(x,y,"or");%绘制一下点
xx = 0:0.01:2*pi;%这个是查询点的坐标向量
yy = interp1(x,y,xx,'pchip');  %yy就是查询点向量对应的函数值向量了,注意最后的参数
plot(x,y,"o",xx,yy,"r");%画图画图

xx=1.23;%只查询一个元素也是可以的
yy = pchip(x,y,xx);%嗯，也可以这样
plot(x,y,"o",xx,yy,"or");%画图画图

对了，三次埃尔米特插值函数在matlab中使用时，最少需要四个插值点。

三次样条插值

所谓样条曲线，就是把一根具有弹性的细长木条(样条)在几个样点处用压铁压住，其余位置自由弯曲。这样子，由样条形成的曲线就称之为样条曲线。样条曲线实际上是由分段三次曲线连接而成，且在连接点处具有连续的二阶导数，从数学上加以概括就得到三次样条的概念。

三次样条函数相对于三次埃尔米特插值，又增加了一些条件。假设三次样条函数。那它除了满足，也就是经过已知点之外，还需要满足，也就是每一段的端点重合。

除此之外，还需要满足，也就是在端点处一阶光滑。以及，也就是端点处二阶光滑。我们可以看出，相对于埃尔米特插值，不仅有一阶导数的要求，也有二阶导数的要求。因此相对于埃尔米特插值，样条插值得到的曲线更加光滑。

以上这些等式条件，提供了个方程(可以自己数数)，但如果我们需要个三次多项式，就需要解出个未知数，也就是需要个方程。剩下的两个方程，我们称之为边界条件。

边界条件主要有三类：

第一类边界条件：给定函数在端点处的一阶导数，即。
第二类边界条件：给定函数在端点处的二阶导数，即。当时，该条件称之为自然边界条件。
第三类边界条件：若是一个周期函数，且是一个周期，则要求也是一个周期函数，满足。

在matlab中，如果三次样条插值没有边界条件，最常用的方法就是采用非结终止条件进行插值。该条件要求第一个和第二个三次多项式的三阶导数相同，以及倒数第一个和倒数第二个三次多项式的三阶导数值相同。使用的函数可以是，也可以是。同样的，至少要求四个点已知。

x = 0:2*pi;  %生成[0,2*pi]之间的整数值
y = sin(x);  %生成相应的函数值
plot(x,y,"or");%绘制一下点
xx = 0:0.01:2*pi;%这个是查询点的坐标向量
yy = interp1(x,y,xx,'spline');  %yy就是查询点向量对应的函数值向量了,注意最后的参数
plot(x,y,"o",xx,yy,"r");%画图画图

xx=1.23;%只查询一个元素也是可以的
yy = spline(x,y,xx);%嗯，也可以这样
plot(x,y,"o",xx,yy,"or");%画图画图

(一段代码用了三次hhh)

如果存在边界条件，则我们使用函数进行三次样条插值。不过具体建模中，往往不会直接给出边界条件，因此函数使用的次数最多。事实上，我们可以发现它的效果还是蛮好的。至于函数的使用，自行查阅啦~