作 者 信 息
赵婵娟,周绍光,丁 倩,刘丽丽
(河海大学 地球科学与工程学院,江苏 南京 211100)
“【摘要】针对高光谱遥感图像分类中标记样本难获取的问题,提出了一种基于同质区和迁移学习的新型半监督分类方法。首先对高光谱图像进行分割得到高纯度的同质分割斑块,获取大量扩展训练样本。并在此基础上引入迁移学习,将扩展训练样本作为源域,剩余未标记样本作为目标域,实现多次迁移,从而减少同一幅图像上各地物的分布差异,并保留其各自的内部属性。实验结果表明,该方法是一种有效的高光谱图像半监督分类方法。
【关键词】高光谱图像分类;图像分割;半监督;迁移学习
【中图分类号】TP79 【文献标识码】A 【文章编号】1672-1586(2019)05-0045-08
”引文格式:赵婵娟,周绍光,丁 倩,等. 基于同质区和迁移学习的高光谱图像半监督分类[J].地理信息世界,2019,26(5):45-52.
正文
0 引 言
近年来,遥感技术和机器学习的进步使高光谱数据得到了广泛应用。其中,高光谱图像分类是遥感领域研究的重要问题之一。在实际应用中,由于大量样本的标记难以获取,未标记的样本有很多且更易获得。因此,如何利用大量未标记样本信息进行分类器的学习,提高其泛化能力,成为当前的研究热点。半监督分类由于能够充分利用少量标记样本和大量无标记样本,并获得更高的分类精度,引起了研究者的高度关注。半监督分类在实践中具有很大的应用价值,一般来说,在半监督学习中,5种模型被广泛使用。主要包括生成式模型、自训练、协同训练、直推式支持向量机和基于图的方法。
上述这些半监督分类方法,通常假设数据的生成机制不随环境改变,即训练样本和测试样本概率分布一致或者位于同一特征空间。若数据分布有差异会造成这些方法的分类效果变差。而我们获得的许多有标记样本的遥感图像可能不满足这个条件,直接用于构建待分类遥感图像的分类器效果不是很理想,若重新标记新的数据来训练模型以适应新的数据分布,代价太高且费时费力。针对这一问题,本文提出了一种基于同质区和迁移学习的半监督高光谱图像分类方法。首先对高光谱图像进行分割获取纯度较高的同质区斑块,然后将有标记样本点所在斑块作为源域,剩余未标记样本作为目标域,实现多次迁移,减少同一图像中各地物的分布差异,最终完成对目标域中大量未标记样本的分类。实验结果表明,可以得到较好的分类效果。
1 同质区获取
本文是以图像分割生成的同质区斑块为基础,基于同质区特性,可以在少量标记样本的基础上获取大量可靠的扩展训练样本,实现对分类器的有效训练。首先,本文通过波段选择的方法选出高光谱图像中3个差异性最大的波段,利用这3个波段对高光谱图像进行Meanshift初始分割,该算法是一种特征空间分析方法,其显著优点是计算量小且简单易实现,是一种有效的统计迭代算法。得到图像的初始分割斑块后,分析斑块的分割纯度不够高,故对这些斑块进行进一步的提纯,算法流程如下(其中center代表中心点,value代表偏移矩阵,S代表中心点的偏移之和):
1)以光谱特征为计算标准,计算所有像素点的特征均值,作为中心点center1;
2)依次计算各像素点和中心点的特征差,并由低到高进行排序得到偏移矩阵;
3)选取偏移矩阵的前40%的像素点,计算其特征均值作为新的中心点center2;
4)计算center2与center1的特征差值的和S;
5)若S大于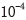 ,则重复步骤2)~4),直至S达到收敛;
,则重复步骤2)~4),直至S达到收敛;
6)最后选取与特征中心点差值不超过最大差值的60%的点作为斑块的同质点。
高光谱图像经过初始分割和提纯后,剩余残留的影像部分大多是比较杂乱的地物区和类别边界处,故对于剩余被剔除的遗留影像,采用超像素分割(Simpl Linear Iterative Clustering,SLIC),将分割数目增多,使得生成的超像素尺寸足够小,从而确保同质区斑块的分割纯度。最终,将像素小于2的斑块与邻近相似度最高的斑块进行合并,得到最终的同质区斑块。
2 结合同质区和迁移学习的半监督分类
2.1 迁移成分分析
本文选取的迁移学习方法是迁移成分分析(Transfer Component Analysis,TCA),其主要解决迁移学习中概率分布问题,是领域自适应(Domain Adaptation,DA)的基本方法之一,该方法基于这一假设:源域和目标域边缘分布不同,即P (XS )≠P (XT ),直接用传统的机器学习方法会导致最终的分类效果较差。故假设存在一个特征映射,使得映射后数据的边缘分布P (Φ(XS))≈P (Φ(XT)),更进一步,条件分布P (YS|Φ(XS))≈P (YT|Φ(XT )),从而实现源域和目标域的适配,最小化两者之间的距离,最终得到各自表达的新特征。在此基础上,便可利用传统的SVM分类器,训练有标注的源域数据DS ={XS ,P (XS)},标定完全无标注的目标域DT ={XT ,P(XT)}。
其中,TCA利用了一个经典的距离叫做最大均值差异(Maximum Mean Discrepancy,MMD)。它是再生希尔伯特空间中两个分布之间距离的度量,其计算公式如下:
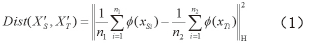
将该式平方展开后如下:
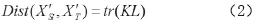
式中,引入了核矩阵: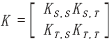 以及L矩阵:
以及L矩阵: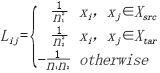 ,这是一个数学的半定规划(Semi-definite Programming,SDP)问题,解决起来非常耗时,为了减少运算时间,TCA的第一作者SinnoJialin Pan采用了降维的思想:
,这是一个数学的半定规划(Semi-definite Programming,SDP)问题,解决起来非常耗时,为了减少运算时间,TCA的第一作者SinnoJialin Pan采用了降维的思想:
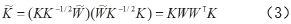
这里的W 矩阵是比K 更低维度的矩阵,即为最后所求。
最终,TCA的优化目标如下:
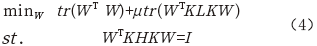
式中,H为中心矩阵: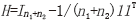 。通过求解该式的拉格朗日对偶,最后转化为求解
。通过求解该式的拉格朗日对偶,最后转化为求解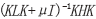 的前m 个特征值,即为W 矩阵的解。最终得到源域和目标域降维后的数据,即经过变换后的新特征。
的前m 个特征值,即为W 矩阵的解。最终得到源域和目标域降维后的数据,即经过变换后的新特征。
2.2 本文算法Semi-TCA
本文将同质区与迁移成分分析算法结合进行改进,完成对高光谱图像的半监督分类。基于同质区特性,各同质区斑块均属于同一类别,故将有标记样本点所在斑块点全部赋予该类标签,即可得到大量扩展训练样本,并将其作为源域;剩余斑块均不含有标记样本,作为目标域。其中,目标域样本远超过源域样本,若直接参与迁移成分分析变换,会由于两边样本不均衡,造成迁移效果变差;同时,TCA需要计算大的核矩阵,核矩阵大小是由源域和目标域数据共同定义的,目标域样本数太大也会造成TCA的计算复杂度变高。
基于此,本文将目标域中各同质区斑块视为一个整体,从各斑块中随机选取任一样本代替所在同质区,从而将目标域样本数减少为同质区的斑块数,大大减少了迁移成分分析变换的计算量。由于随机选取一点的稳定性不高,故采取多次迁移的方法增加实验的稳定性,并获得目标域各同质区的预测标签集,采取最大投票法,选择类别占比最多的那一类作为各斑块的最终标签值。最终,将各斑块的标签全部赋予给斑块里所有的样本,由此获得目标域所有样本点的预测标签,完成全图分类。
本文算法的具体实现步骤如下所示:
基于同质区和迁移学习的半监督分类算法(Semi-TCA):
输入:源域数据集(Xs ,Ys ),目标域同质区斑块Block ,投影子空间维数m ,正则化系数μ ,基分类器ƒ,目标域斑块随机选点次数T。
输出:目标域所有样本点的预测标签Yt。
1)for i =1 to T do;
2)在目标域各同质区斑块中随机取一点构成目标同质区样本集: Xb;
3)计算核矩阵K ,根据式(4)求解投影变换矩阵W;
4)将源域数据集特征Xs 和目标同质区样本特征Xb进行TCA变换,映射到m维子空间中,从而得到变换后的新特征Xs '和Xb ';
5)在数据集(Xs ',Ys )上训练基分类器ƒ,利用训练得到的分类器对Xb '进行标记,得到目标同质区斑块本次训练对应的预测标签Ybi;
6)end for;
7)最终得到目标同质区T 次迁移的预测标签集Yb _set={Yb 1,Yb 2,...,YbT };
8)采取最大投票算法,得出同质区各斑块的最终标签Yb _last=Moore's voting(Yb _set);
9)将同质区预测标签Yb _last分别赋予给所在斑块内所有样本点,求得目标域所有样本的预测标签Yt。
3 实验结果与分析
3.1 实验环境
实验均在Matlab 2017b软件平台下进行,操作系统为Windows 10 64位系统,处理器为Intel(R)Core(TM)i5-8400,CPU:@2.80Ghz 2.81 Gh,内存为32 GB。
3.2 实验数据
1)Indian Pines数据
该数据是于1992年在美国印第安纳州西北部的印第安松树林试验区通过AVIRIS传感器获取的。图像尺寸为145×145 pixel,光谱范围0.4~2.5μm,空间分辨率为20 m。该数据包含220个波段,去除20个水汽吸收波段、低信噪比波段,保留其中的200个波段进行分类。该数据共包含16类地物共10 249个标记样本,各类标记样本个数见表1。图1为Indian Pines高光谱图像的假彩色合成图像及地面真实标记数据。
表1 Indian Pines数据的地物类别及样本数目
Tab.1 Species and sample sizes of Indian Pines data
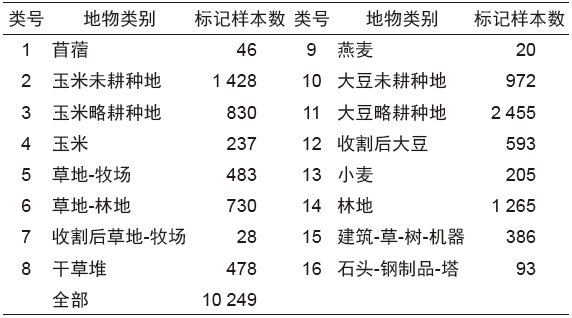

图1 AVIRIS Indian Pines数据集
Fig.1 AVIRIS Indian Pines dataset
2)Pavia University 数据
本文采用的数据是由成像光谱仪ROSIS-3采集的意大利帕维亚大学高光谱遥感图像。该数据的空间分辨率为1.3 m,光谱范围0.43~0.86μm。该数据包含115个光谱波段,图像尺寸为610×340 pixel,实际使用去除噪声波段后的103个波段进行分类。该高光谱图像的假彩色合成图像及参考分类图像如图2所示,从图2中可以看出该数据包括9种地物类别,该数据的地物类别具体情况见表2,共42 776个样本。
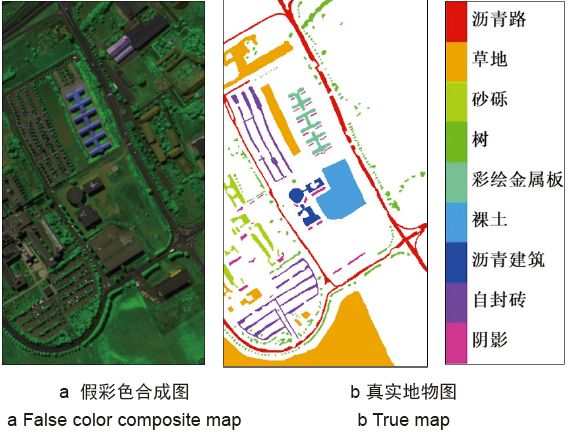
图2 ROSIS帕维亚大学数据集
Fig.2 ROSIS Pavia University dataset
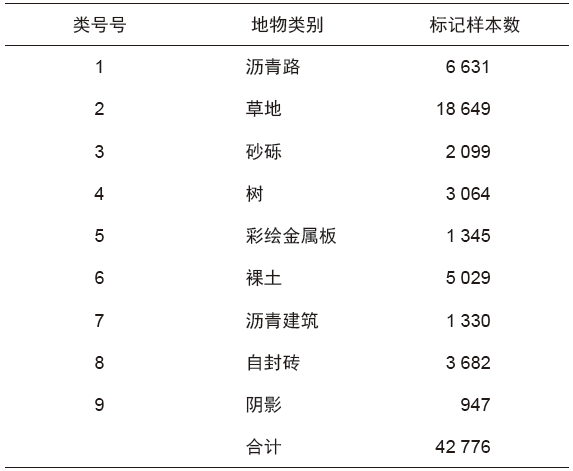
表2 Pavia University数据的地物类别及样本数目
Tab.2 Species and sample sizes of Pavia University data
3.3 实验设置
本次实验主要分为两部分:一是对两种高光谱图像进行相应的图像分割,从而获取较纯的同质区分割斑块。二是基于分割好的同质区进行相关实验,将本文算法Semi-TCA与SVM、Semi-HRS以及Binge Cui等人提出的ELP-RGF方法进行对比。
1)SVM是第一个基准对比方法,直接利用初始标记样本训练SVM分类器,对全图未标记样本进行测试得到分类结果。
2)Semi-HRS是第二个基准对比方法,训练样本为基于同质区得到的扩展训练样本,将除初始标记样本剩余的未标记样本作为测试样本。
3)ELP-RGF是一种基于图的半监督分类算法,首先将标记样本信息传播到相邻的未标记样本,其次使用超像素将相同的标签分配给超像素内的所有像素,以此来增大训练样本的数量。
在图像分割实验中,由于IP图像较小,故对IP图像最终进行超像素分割的斑块数设为1 000,而PU图像较大,故设为8 000。
在分类实验中,每类分别随机选取5、10、15个有标记样本点作为初始训练样本。本文算法Semi-TCA主要涉及3个参数,正则化系数λ、映射后的空间维度dim和目标域各斑块随机选点的次数T ,根据参数调优实验得出最优参数λ 为0.1,dim 设为90,选点次数T 设为11。训练样本和Semi-HRS一致,均为扩展训练样本,除去初始训练样本,剩余有标记的样本点全部作为评价样本进行测试。其中,所有算法均采用线性的支持向量机分类器(LinearSVM),并采用总体分类精度(Overall Accuracy,OA)、平均精度(Average Accuracy,AA)和Kappa 系数作为评价指标,为提高实验的精确度和可靠性,独立重复进行10次实验,每次均随机选取初始训练样本,将10次实验结果的分类精度求取平均值作为各类算法的最终的分类精度。
3.4 实验结果与分析
3.4.1 Indian Pines数据集实验结果与分析
在该数据集下,图像分割的过程如图3所示,其中,在超像素分割之后,又将像素小于2的斑块与邻近相似度最高的斑块进行了合并,从而得到最终的同质区,同质区斑块数为842,分割精度为98.02%。
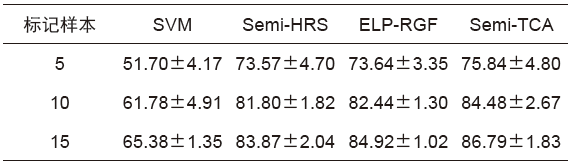
表3为Indian Pines数据在选定标记点相同的情况下不同方法得到的分类结果的总体精度,其表达形式是平均值±标准差。经过对比分析发现:随着每类标记样本个数的增加,各算法的分类精度也在不断提升,而本文提出的半监督分类方法在选定标记点数目不同时,其分类精度总是优于其他对比方法。

图3 Indian Pines图像分割形成同质区斑块的过程
Fig.3 The process of Indian Pines image segmentation to form plaques in homogeneous regions
表3 Indian Pines数据集在不同标记样本下的总体分类精度(分类精度±标准差)(%)
Tab.3 Overall classification accuracy of the Indian Pines dataset under different labeled samples (classification accuracy ± standard deviation)(%)
为了证明本文提出的算法的有效性,我们考虑最困难的情况,即每类地物仅只有5个有标记样本的情况。因为有标记样本点越少,分类就越难。从表4中可以看出,当每类只选取5个标记点时,本文算法Semi-TCA总体分类精度OA相比SVM、Semi-HRS和ELP-RGF分别高24%、2%和2%。此外,Kappa 系数也为最高,图4为该情况下各算法的全图分类效果图。红色圆圈内区域,可以看出本文算法的错分噪声点明显减少,在一定程度上体现了本文算法的优势。
表4 Indian Pines各类地物在不同算法下的分类精度(分类精度±标准差)(%)
Tab.4 Classification accuracy of various species of Indian Pines by different algorithms (classification accuracy ± standard deviation) (%)
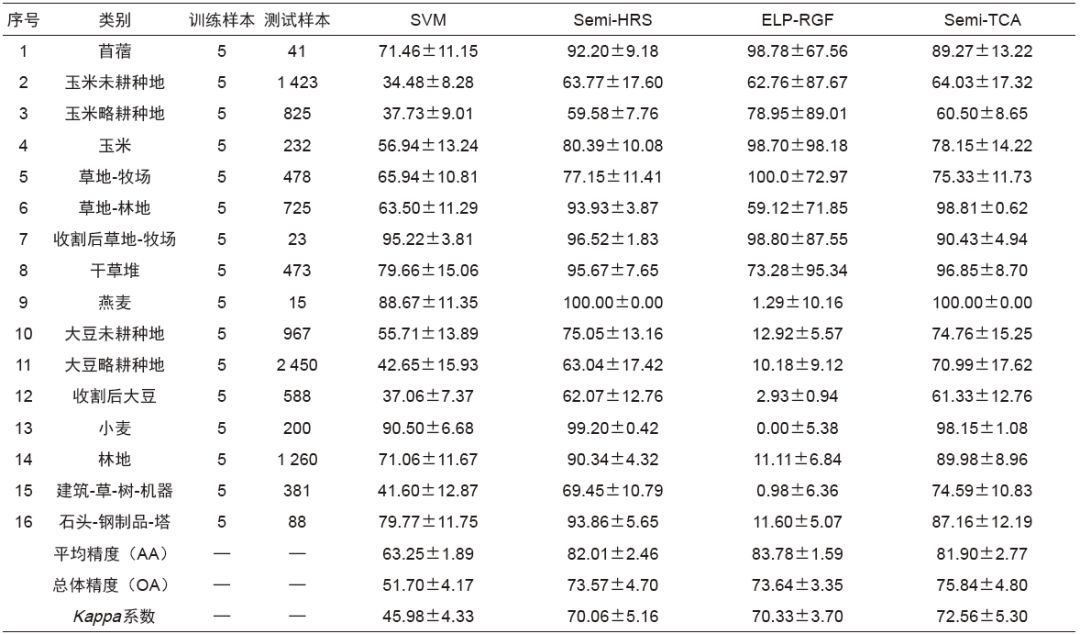
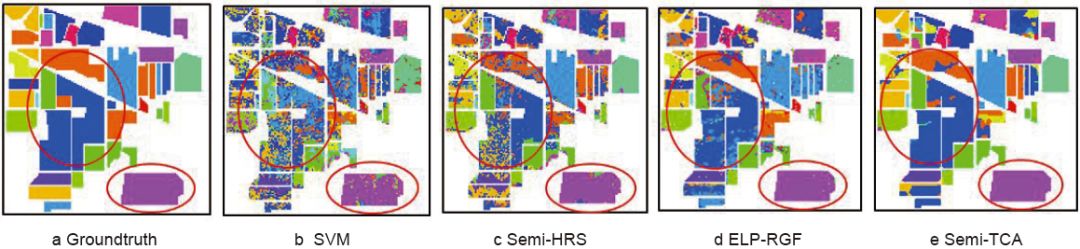
图4 各算法在Indian Pines上的一组实验的分类识别图
Fig.4 Classification identification map of a set of experiments for each algorithm on Indian Pines
3.4.2 Pavia University数据集实验结果与分析
Pavia University数据集的图像分割的过程如图5所示,与Indian Pines数据集不同的是合并了像素小于5的斑块,从而增加各同质区的面积,最终分得的同质区斑块数为6 325,分割精度为99.79%。

图5 Pavia University图像分割形成同质区斑块的过程
Fig.5 The process of Pavia University image segmentation to form plaques in homogeneous regions
表5为Pavia University数据在每类地物取5、10、15个标记样本情况下各算法的平均总体精度。经过对比分析发现:在不同的标记样本数目下,本文算法Semi-TCA的分类精度总是优于其他对比方法,当每类标记样本为15时,达到93%较好的总体分类精度。
表5 Pavia University数据集在不同标记样本下的总体分类精度(分类精度±标准差)(%)
Tab.5 Overall classification accuracy of the Pavia University dataset under different labeled samples (classification accuracy ± standard deviation)(%)
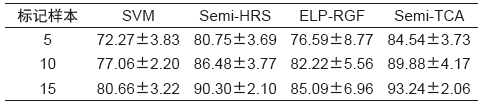
表6为每类只选取5个标记点时,各类地物的分类精度,本文算法的总体分类精度OA、平均精度AA和Kappa系数相比其他3种对比方法均为最高。其中,本文算法对于沥青路、草地、砂砾等地物的分类精度都比其余3种算法高约3%~20%,这是因为这类地物在图像中呈现大片块状均匀分布,非常有利于构建源域和目标域的相关联系,减少两者之间的差异,从而提取出更有判别力的低维特征。图6为各算法的全图分类效果图。红色圆圈内区域,可以看出本文算法的错分点最少,分类效果最好。
表6 Pavia University数据数据集各类地物在不同算法下的分类精度(分类精度±标准差)(%)
Tab.6 Classification accuracy of various species of Pavia University by different algorithms (classification accuracy ± standard deviation) (%)
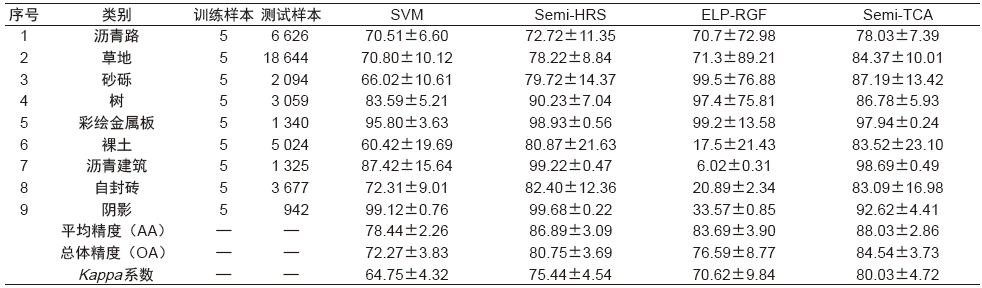
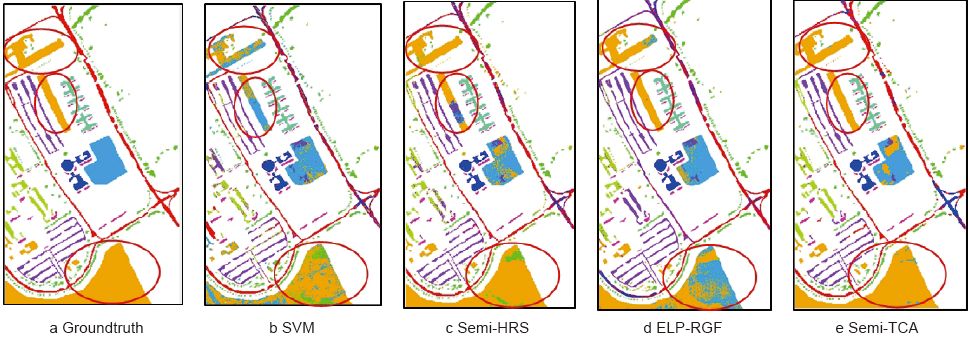
图6 各算法在 Pavia University 上一组实验的分类识别图
Fig.6 Classification identification map of a set of experiments for each algorithm on Pavia University
4 结束语
针对高光谱图像中标记样本点少,无法训练出完备分类器这一问题,本文提出了一种基于同质区和迁移学习的半监督分类方法。
1)同质区的使用,可以克服标记样本数量少的困难,利用同质区特性可以扩展大量训练样本,充分利用无标记样本信息参与分类器的训练,从而构建出更完备,泛化性能更好的分类器。
2)在同一幅高光谱图像中,采取迁移学习的方法,将图中有标记样本区域迁移至无标记样本区域,最小化它们之间的分布差异,可以在原有较好的分类效果上进一步提升。
实验结果表明,本文算法在两组实际高光谱图像分类中都取得优于其他对比方法的分类精度。由于本文算法需要多次迁移且计算复杂度较高,故存在运行时间较长的缺点,进一步的研究可以针对迁移学习算法的计算量做一些改进,同时,如何更好地减少同一幅影像上的分布差异也有待探索。
本期回顾
文化遗产数字化修复
· 机载LiDAR点云建筑物屋顶轮廓线自动提取研究综述
· 融合多特征的兵马俑碎片分类技术研究
· 基于高光谱影像的瞿昙寺壁画颜料层脱落病害评估
理论研究
· 兼顾非期望产出的工业用地效率测度、分异与溯因 ——以东北三省为例
· 基于模体的化石能源贸易网络特征分析
· 基于自编码网络的移动轨迹异常检测
邮箱变更声明
·《地理信息世界》邮箱变更声明
网站开通公告
·关于开通《地理信息世界》网站的公告
诚聘特约审稿专家
·诚聘|《地理信息世界》诚聘特约审稿专家
专题组稿
·约稿函|《地理信息世界》关于开辟“博士综述论坛”专栏的约稿函





![【题解】Luogu P4052[JSOI2007]文本生成器 AC自动机](http://pic.xiahunao.cn/【题解】Luogu P4052[JSOI2007]文本生成器 AC自动机)

...)



2019年9月计算机二级C语言试题)

学习随笔:toolButton的popupMode属性)



)





方法匹配多个关键字的方法)
