二叉搜索树中第k大元素

Problem statement:

问题陈述：

Find the k-th smallest element in a given binary search tree (BST).

在给定的二进制搜索树(BST)中找到第k个最小的元素。

Example:

例：

    K=4
Kth smallest element in the above binary tree is: 6
K=5
Kth smallest element in the above binary tree is: 7

Solution:

解：

One possible solution is to store the in-order traversal of the BST and printing the Kth element from the list. This can be done because in-order traversal of the BST produces a sorted list. But this solution leads to the overhead of additional storage which may not be entertained.

一种可能的解决方案是存储BST的有序遍历并从列表中打印第K个元素。 之所以可以这样做是因为BST的有序遍历会生成一个排序列表。 但是该解决方案导致可能无法解决的额外存储的开销。

So, we go for a much better solution where we don’t need any additional space.

因此，我们寻求了一个更好的解决方案，不需要任何额外的空间。

Algorithm:

算法：

//k, count both parameter are passed by reference
FUNCTION kthSmallest (root, int & k, int &count) 
1.  Base case
IF (root is NULL)
Return 0;
2. Carry out in-order traversal and keep checking for kth smallest element.
left=kthSmallest (root->left, k, count) //for left subtree
IF (left)
return left;
Increment count
IF (count==k)
return root->data; //kth smallest element
kthSmallest(root->right,k,count); //for right subtree
In the main function we call kthSmallest (root, k, 0) //count 0 initially

Example with explanation:

带有说明的示例：

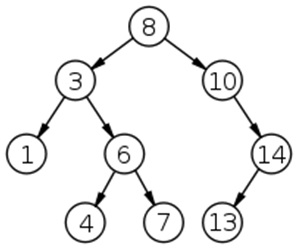
    In the main function we make call to kthSmallest(root, 4, 0)
-------------------------------------------------------------
KthSmallest (8, 4, 0)
8 not NULL
Left= KthSmallest(8->left , 4, 0);
Call to KthSmallest(3 , 4, 0): //8->left=3
-------------------------------------------------------------
KthSmallest (3, 4, 0)
3 not NULL
Left=KthSmallest(3->left , 4, 0);
Call to KthSmallest(1 , 4, 0): //3->left=1
-------------------------------------------------------------
KthSmallest (1, 4, 0)
1 not NULL
Left= KthSmallest(1->left , 4, 0);
Call to KthSmallest(NULL , 4, 0): //1->left=NULL
-------------------------------------------------------------
KthSmallest (NULL, 4, 0)
node is NULL
return 0;
-------------------------------------------------------------
Control back to KthSmallest (1, 4, 0):
Left=0
Increment count
Count=1;
K!=count
Call to kthSmallest(1->right, 4, 1) 
-------------------------------------------------------------
This is again NULL and control backs to KthSmallest (1, 4, 0)
Since end of function reached control backs to KthSmallest (3, 4, 0)
KthSmallest (3, 4, 0):
Increment count
Count=2 //it’s not 1 because count is passed by reference
K!=count
Call to KthSmallest(3->right, 4, 2)

So if you carry out similar way you will be able to find the k-th smallest one once k==count

因此，如果执行类似的方法，则一次k == count就能找到第k个最小的 整数

C++ implementation:

C ++实现：

#include <bits/stdc++.h>
using namespace std;
// tree node is defined
class Node{
public:
int data;
Node *left;
Node *right;
};
// creating new node
Node* newnode(int data)  
{ 
Node* node = (Node*)malloc(sizeof(Node)); 
node->data = data; 
node->left = NULL; 
node->right = NULL; 
return(node); 
} 
//finding kth smallest element
int kthSmallest(Node *root, int& k,int &count){ 
if(!root)
return 0;
int left=kthSmallest(root->left,k,count);	
if(left)
return left;
count=count+1;
if(count==k)
return root->data;
kthSmallest(root->right,k,count);
}
int main()
{
//building the bst
int count=0,k;
Node *root=newnode(8); 
root->left= newnode(3); 
root->right= newnode(10); 
root->right->right=newnode(14);
root->right->right->left=newnode(13);
root->left->left=newnode(1); 
root->left->right=newnode(6);
root->left->right->left=newnode(4);
root->left->right->right=newnode(7);
cout<<"input k\n";
cin>>k;
cout<<"Kth smallest element in the ";
cout<<"binary tree is :"<<endl; 
cout<< kthSmallest(root,k,count);
return 0;
}

Output

输出量

input k
4
Kth smallest element in the binary tree is :
6

翻译自: https://www.includehelp.com/icp/k-th-smallest-element-in-a-binary-search-tree.aspx

二叉搜索树中第k大元素