3.1_正规文法和状态转换图

（1）构造状态转换图

1、对于G中每一个形如A——>aB的产生式，从结点A引一条矢线到结点B，并用符号a标记这条矢线
即A—^a—>B

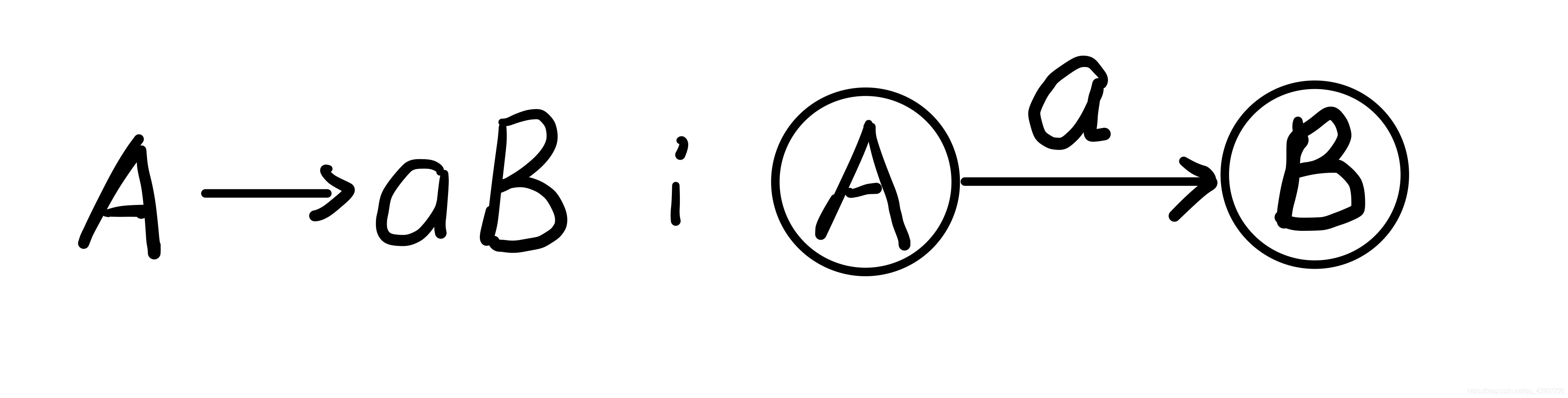
2、对于G中每一个形如A——>a的产生式，从结点A引一条矢线到结点F，并用符号a标记这条矢线
即A—^a—>F

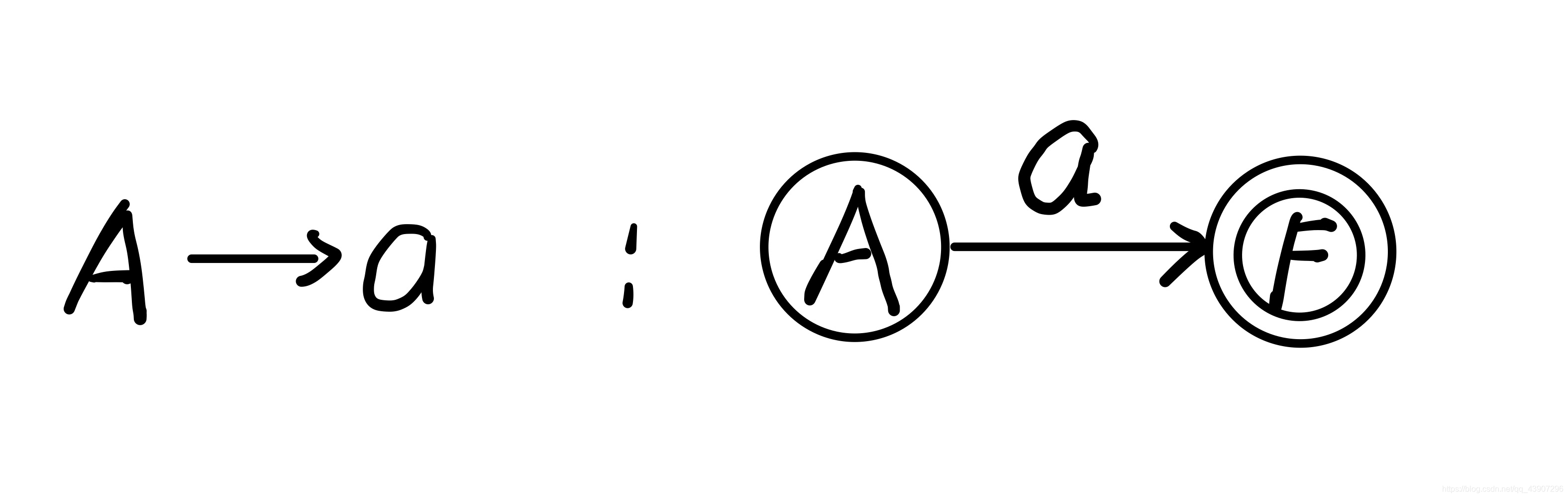
（2）状态矩阵

状态矩阵：Bij=B[Si，aj]，其中Si为状态图中各状态，aj为各输入符号，总元素个数＝|VN|×|VT|

3.2_有限自动机

3.2.1_确定的有限自动机DFA

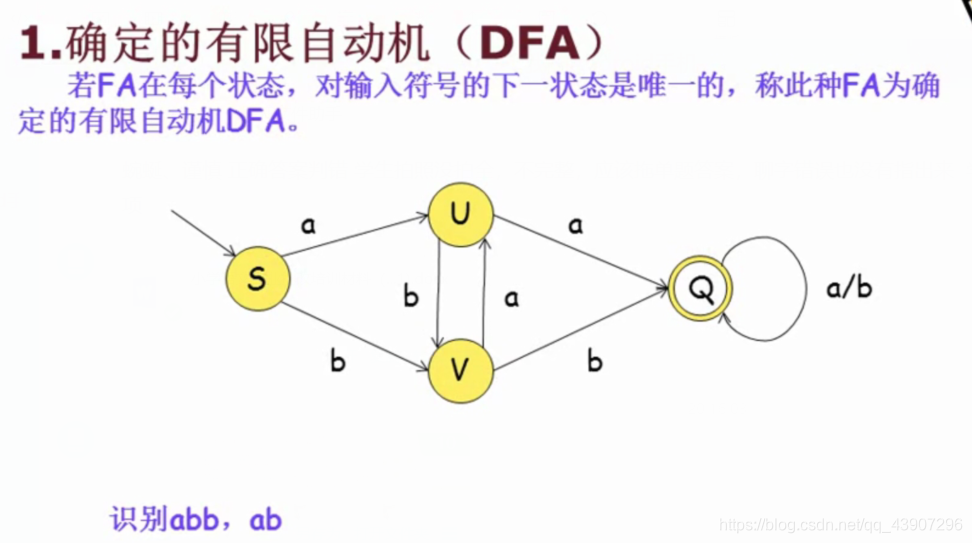
3.2.2_非确定的有限自动机NFA

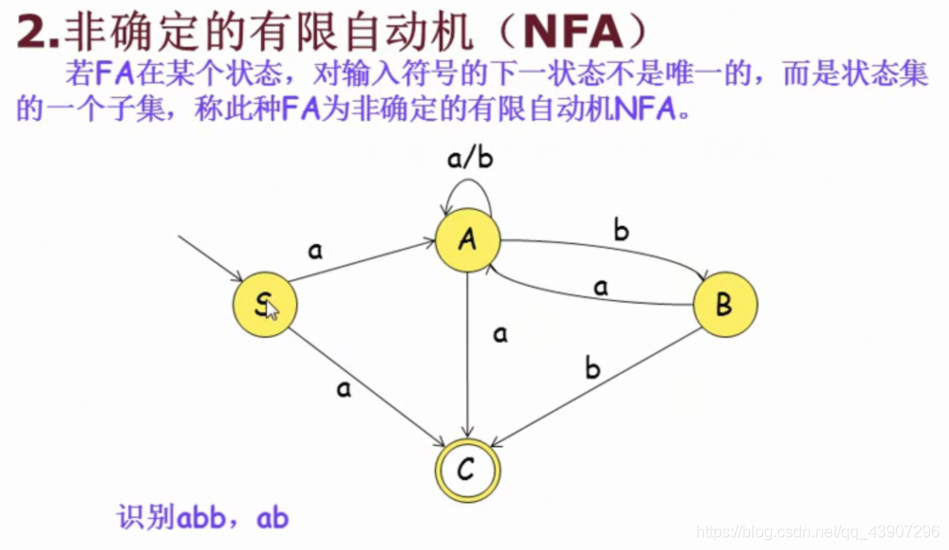
3.3_NFA转换为DFA（NFA确定化）

3.3.1_无ε动作的NFA确定化

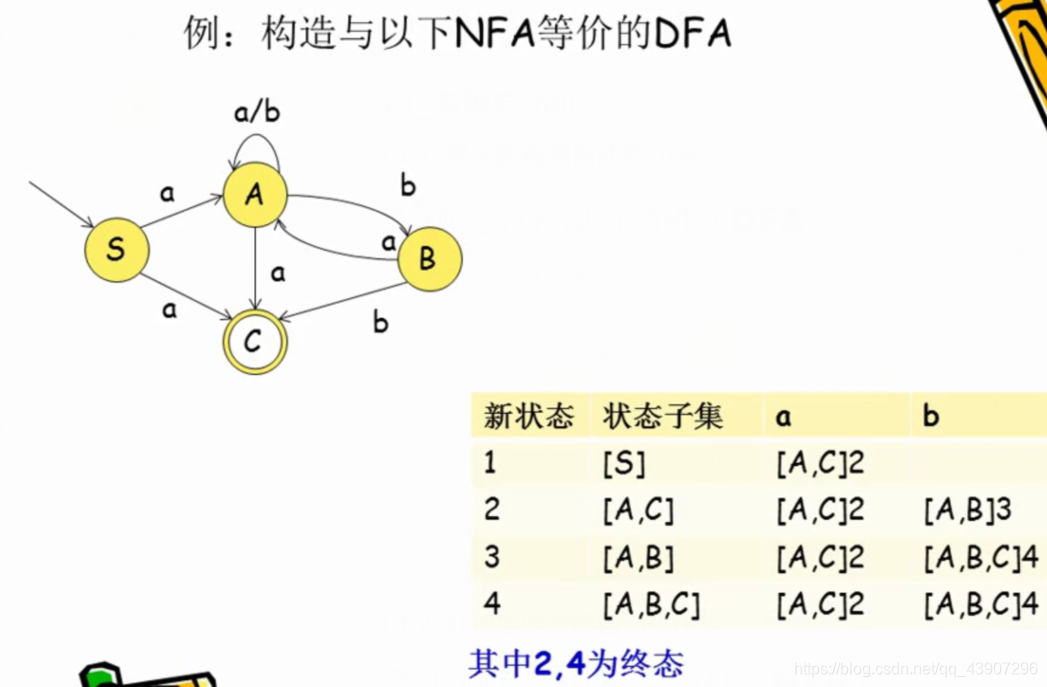
3.3.2_有ε动作的NFA确定化

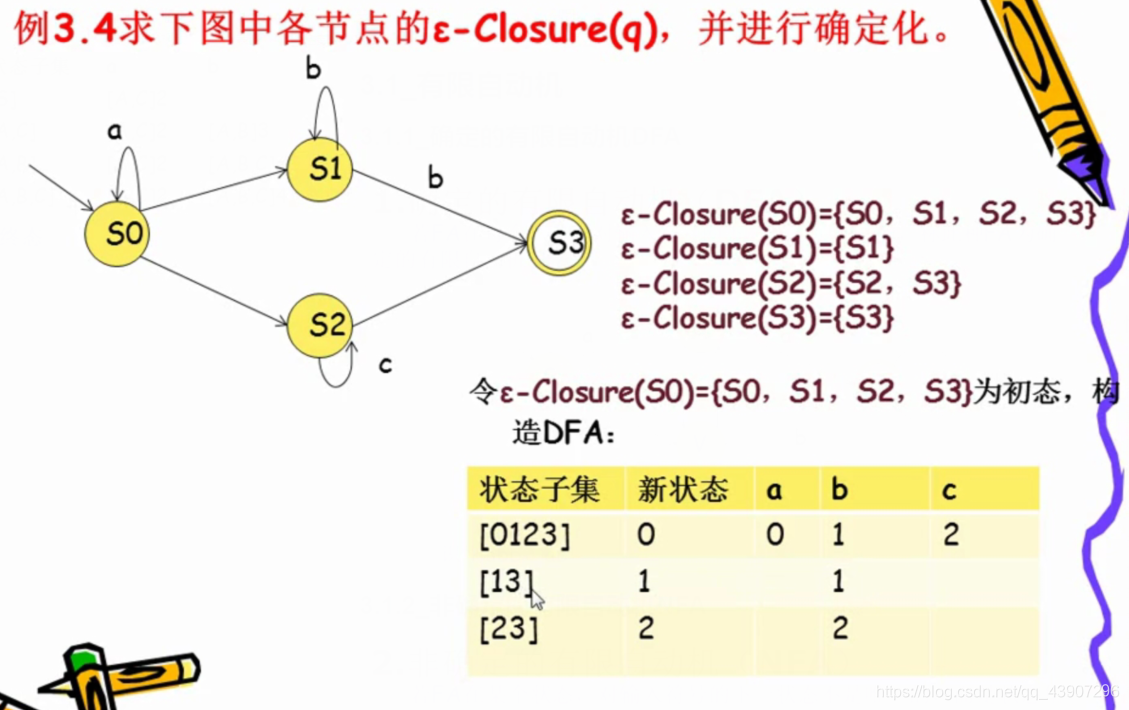
3.4_DFA最小化

DFA状态数最小化算法:
(1)将状态集K划分为终态子集Z和非终态子集K-Z， 记为π={Z, K-Z}。
(2)对当前中的每个子集，检查其中每个状态对识别相同字符是否具有同样的映射（即是否能够映射到π中的同一个集合），将映射到不同状态子集的称为可以区分的，将其按映射关系进行分裂，产生新的状态子集集合，记为πnew。 .
(3)若πnew <> π， 重复(2)，直至各子集都不能继续划分。
(4)对最终划分II的每个状态子集，取其中任一状态作为该子集的代表状态，将原来射入该子集的所有矢线改为射入此代表状态。取含有原任一终态的子集作为新的终态。

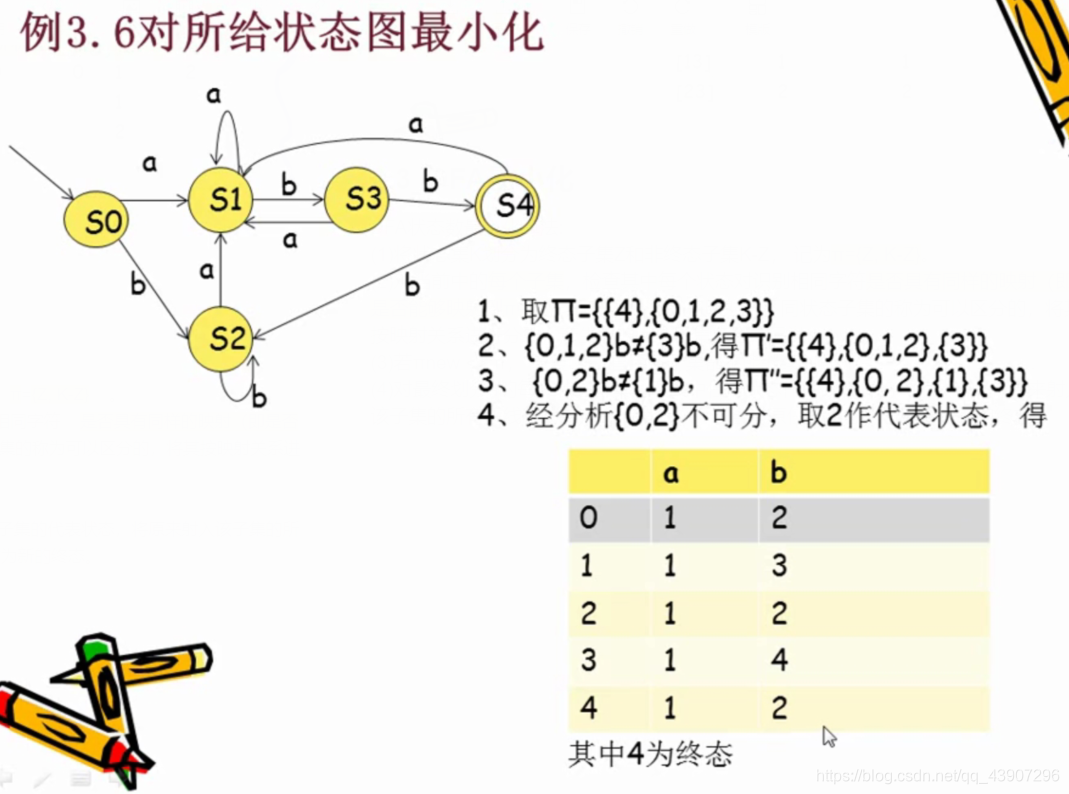
3.5_正规表达式和正规集

（1）正规式:将文法的终结符号用以上三种运算符连接起来组成的正规文法的表达式，是另- -种用于描述正规文法的直观表示。
例如语法范畴<标识符>的正规表达式为:字母(字母|数字) *
（2）正规集:正规式所描述的字符串的集合。