有重复数字的组合问题_带数字重复的组合和问题

有重复数字的组合问题

Description:

描述：

This is a standard interview problem to make some combination of the numbers whose sum equals to a given number using backtracking.

这是一个标准的面试问题，它使用回溯功能将总和等于给定数字的数字进行某种组合。

Problem statement:

问题陈述：

Given a set of positive numbers and a number, your task is to find out the combinations of the numbers from the set whose summation equals to the given number. You can use the numbers repeatedly to make the combination.

给定一组正数和一个数字，您的任务是从集合中找出总和等于给定数字的数字组合。您可以重复使用数字进行组合。

    Input:
Test case T
T no. of N values and corresponding N positive numbers and the Number.
E.g.
3
3
2 3 5
12
3
2 7 5
14
4
1 2 3 4
5
Constrains:
1 <= T <= 500
1 <= N <= 20
1 <= A[i] <= 9
1 <= Number<= 50
Output:
Print all the combination which summation equals to the given number.

Example

例

    Input:
N=3
Set[ ]=2 3 5
Number=12
Output:
2 2 2 2 2 2
2 2 2 3 3
2 2 3 5
2 5 5
3 3 3 3

Explanation with example:

举例说明：

Let there is a set S of positive numbers N and a positive number.

设一组正数N和一个正数S。

For pre-requisite, we are recommending you to go to our article combinational sum problem.

对于先决条件，我们建议您转到我们的文章组合总和问题。

Making some combinations repeatedly using a number in such a way that the summation of that combination results that given number is a problem of combination and we will solve this problem using backtracking approach.

重复使用数字进行一些组合，使得该组合的总和导致给定数字是组合的问题，我们将使用回溯方法解决该问题。

    Let, 
f(i) = function to insert the is^th number into the combinational subset

In this case we will consider two cases to solve the problem,

在这种情况下，我们将考虑两种情况来解决该问题，

We will consider i^th element into the part of our combination subset until the sum greater the given number (f(i)).
我们将考虑^第 i ^个元素进入组合子集的一部分，直到总和大于给定数( f(i) )。
We will not consider ith element into the part of our combination subset (not f(i)).
我们不会在组合子集的一部分( 不是f(i) )中考虑第ith个元素。

And every time we will check the current sum with the number. Each of the time we will count the number of occurrence and the also the combinations.

并且每次我们将用数字检查当前总和。每次，我们将计算发生的次数以及组合。

    Let,
f(i) = function to insert the i^th number into the combinational subset

For the input:

对于输入：

    S[] = {2, 3, 5}
Number = 12

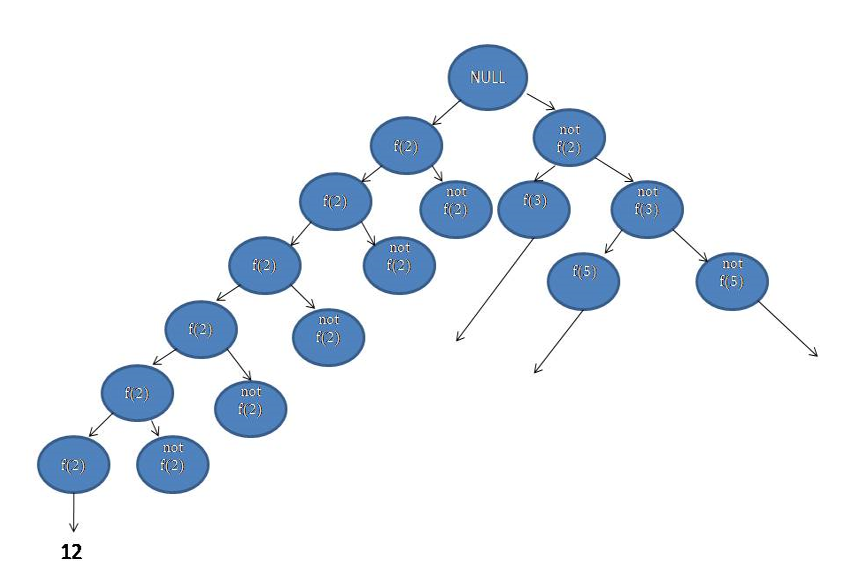
Combinational sum problem with repetition of digits

Here from every (not f(2)) there will be two edges (f(3)) and (not f(3)) again from (not f(3)) there will be ( f(5)) and (not f(5)). Here in this case we will discard that edges which have a current sum greater than the given number and make a count to those numbers which are equal to the given number.

在每个(非f(2))中将有两个边(f(3))和(非f(3))从(非f(3))再有(f(5))和(非f(5)) 。在这种情况下，我们将丢弃当前总和大于给定数字的那些边，并对等于给定数字的那些数字进行计数。

C++ implementation:

C ++实现：

#include <bits/stdc++.h>
using namespace std;
void combination(int* arr, int n, int num, int pos, int curr_sum, vector<vector<int> >& v, vector<int> vi, set<vector<int> >& s)
{
if (num < curr_sum)
return;
if (num == curr_sum && s.find(vi) == s.end()) {
s.insert(vi);
v.push_back(vi);
return;
}
//go for the next elements for combination
for (int i = pos; i < n; i++) {
if (curr_sum + arr[i] <= num) {
vi.push_back(arr[i]);
combination(arr, n, num, i, curr_sum + arr[i], v, vi, s);
vi.pop_back();
}
}
}
//print the vector
void print(vector<vector<int> > v)
{
for (int i = 0; i < v.size(); i++) {
for (int j = 0; j < v[i].size(); j++) {
cout << v[i][j] << " ";
}
cout << endl;
}
}
void combinational_sum(int* arr, int n, int num)
{
vector<vector<int> > v;
vector<int> vi;
int pos = 0;
int curr_sum = 0;
set<vector<int> > s;
combination(arr, n, num, pos, curr_sum, v, vi, s);
print(v);
}
int main()
{
int t;
cout << "Test Case : ";
cin >> t;
while (t--) {
int n, num;
cout << "Enter the value of N : ";
cin >> n;
int arr[n];
cout << "Enter the values : ";
for (int i = 0; i < n; i++) {
cin >> arr[i];
}
sort(arr, arr + n);
cout << "Enter the number : ";
cin >> num;
combinational_sum(arr, n, num);
}
return 0;
}

Output

输出量

Test Case : 3
Enter the value of N : 3
Enter the values : 2 3 5
Enter the number : 12
2 2 2 2 2 2
2 2 2 3 3
2 2 3 5
2 5 5
3 3 3 3
Enter the value of N : 3
Enter the values : 2 7 5
Enter the number : 14
2 2 2 2 2 2 2
2 2 5 5
2 5 7
7 7
Enter the value of N : 4
Enter the values : 1 2 3 4
Enter the number : 5
1 1 1 1 1
1 1 1 2
1 1 3
1 2 2
1 4
2 3