朱利判据


其中
{bn−k=an−k−ana0∗akcn−k=bn−k−bnb0∗bk...qn−k=pn−k−pnp0∗pk\begin{cases} b_{n-k}=a_{n-k}-\frac{a_n}{a_0}*a_k\\ c_{n-k}=b_{n-k}-\frac{b_n}{b_0}*b_k\\ ...\\ q_{n-k}=p_{n-k}-\frac{p_n}{p_0}*p_k \end{cases}⎩⎪⎪⎪⎨⎪⎪⎪⎧bn−k=an−k−a0an∗akcn−k=bn−k−b0bn∗bk...qn−k=pn−k−p0pn∗pk
系统稳定的充要条件就是a0,b0,...,q0a_0,b_0,...,q_0a0,b0,...,q0均为正。
可以用Matlab直接在工作区生成朱利表,需要先生成一个带交互式界面的M文件,它的代码主要依赖于Matlab本身的程序语言控制,M文件如下:
disp('利用朱利判据判断离散系统的稳定性')
disp('请输入特征方程的系数矩阵A')
A=input('A=');
n=size(A,2);%截取A的维数
for i=n:-1:1disp(A);%显示奇数行if i==1 if A(:)>0disp('系统稳定');elsedisp('系统不稳定');endbreak;endB=flip(A);disp(B);%显示偶数行if A(1,1)<=0disp('首元素非正!系统不稳定');break;endk=B(1,1)/A(1,1);A(1,:)=A(1,:)-k*B(1,:);A(:,i)=[];%A矩阵减维数
end
保存M文件命名为M1.m
执行的效果如下:
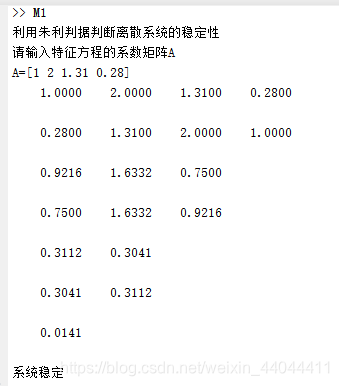


方法与示例)
【Simulink仿真】)

方法与示例)



方法与示例)



方法与示例)


方法与示例)


