1.非参数估计原理

\qquad已知一个样本的概率分布时，我们只需要对概率分布中的参数进行估计即可得到该样本的概率密度函数。例如已知样本X服从正态分布$N(\mu ,\sigma )$，通过样本对$\mu ,\sigma$进行估计。然而并不是每个样本的概率分布都是已知的，很多情况下我们只有样本但是没有概率分布模型。这个时候我们仍然要知道每个点的概率密度，这该怎么办呢？
\qquad概率密度函数$p(x)$实际上是概率分布函数$F(x)$的导数，概率分布函数是样本在一定范围内分布的总概率，我们可以利用这个思想去求取每个点的概率密度。首先，我们以我们想求概率密度的点$x_0$为中心，作超球体S（因为可能超过三维，因此称为超球体，广义的超球也包括了线段、圆、球），设S包含的体积为V，总样本数为N，有k个样本包含在超球体V中。则概率分布函数
$$F(x_0,V)=P(X\in S)=k/N$$
当$V\to 0,N\to +\infty$时，$\hat{p}(x_0)=\frac{F(x_0,V)}{V}=\frac{k}{VN}$
事实上，这个取极限的过程没有那么简单，还需要满足以下三个极限等式才能用这个式子表示概率密度：
$$\begin{gathered} \underset{N\to +\infty }{\lim }{V}_N=0 \\ \underset{N\to +\infty }{\lim }{K}_N=\infty \\ \underset{N\to +\infty }{\lim }\frac{k_N}{N}=0 \end{gathered}$$
\qquad为了满足上述三个极限等式，可以取$V_N=h_N/\sqrt{N}$或$K_N=k_N\sqrt{N}$，这样衍生出的两种方法分别是Parzen窗法和$K_N$近邻法。注意因为$V_N$和$K_N$是相互约束的，因此两种设定只能选其一，否则会得到荒谬的结果。

2.Parzen窗

2.1.算法原理

\qquadParzen窗法是指定$V_N$，求取包含在以待估计点$x_0$为中心，区域$R_N$内的（体积$V_N$）内的样本数$k_N$，从而得到该点概率密度的方法。区域$R_N$的函数就叫做窗函数。窗函数的形式有多种，主要分为4种：①超球窗②超立方体窗③正态分布窗④指数分布窗。在这里我们只介绍最常用的正态分布窗。样本点计为x,待求点中心记为$x_0$，令$d=x-x_0$，设球半径为h，距离尺度$u=d/h$。其窗函数$\varphi (u)$如下：
$$\varphi (u)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{u}^2}$$
\qquad我们可以认为每个样本对于空间上的每个点的概率密度都有一定的贡献，但是随着空间点距离样本点的距离增大，这个贡献率会减小。一个样本点对其所在位置的概率密度贡献最大，随着距离样本点的距离会依次减小，这个贡献率分布函数就是由窗函数定量给出的。将每个样本点对所有空间点的概率密度贡献累加，就是空间上的概率密度分布函数，这便是Parzen窗的算法原理。
\qquad注意将每个样本的窗函数累加只是代表$k$的值，即距离空间点最近的k个元素，要想求出概率密度，还需要知道R区域的体积（样本数N是已知的）。在Parzen窗法中，体积V是正比于$\frac{1}{\sqrt{N}}$的一个函数，它需要跟距离尺度u保持一致，使估计概率密度的极限与窗函数系数h无关。因此$V=\frac{h}{\sqrt{N}}$，这样对于空间点$x_0$
$$k=\sum _{i=1}^N\varphi (\frac{X_i-x_0}{h})$$
$$\hat{p}(x_0)=\frac{k}{VN}=\frac{{\sum }_{i=1}^N\varphi (\frac{X_i-x_0}{h})}{\frac{h}{\sqrt{N}}N}=\sum _{i=1}^N\frac{1}{h\sqrt{2\pi N}}{e}^{-\frac{1}{2}\frac{(X_i-x_0{)}^2}{h}}$$
利用上式求出每个空间点的概率密度即可，当然这个空间点选取的密度是认为定的，当样本数目N趋向于∞时，$\hat{p}(x_0)\to p(x_0)$。注意体积V为什么是正比于$\frac{1}{\sqrt{N}}$而不是其他什么关于N的表达式是根据三个极限表达式推导出来的，理论证明部分不再赘述。

2.2.Matlab实现与参数探究

\qquad我们的思路是使用一个已知分布的样本去测试Parzen窗，观察Parzen窗与其概率密度的相似度。我们选用的样本X服从$N(0,1)$分布，需要测试的参数有两个，样本数N和窗宽参数h。我们需要分析随着样本数的变化，Parzen窗的概率密度估计效果，我们选取了$N=2^4,2^8,2^{16}$；另一方面，我们还需分析窗宽参数对拟合效果的影响，这里我们选取了$h=0.5,1,4$，相关的MATLAB代码如下所示：

N=[2^4,2^8,2^16]';
x=-4:0.01:4;
y=1/sqrt(2*pi)*exp(-0.5*x.^2);
h1=[0.5,1,4];
h=h1./sqrt(N);
figure
for Ni=1:length(N) %按照指定样本数序列进行仿真X=normrnd(0,1,1,N(Ni));%生成指定数目特定分布的样本for hi=1:length(h1)  %取指定的h值subplot(length(N),length(h1),(Ni-1)*length(h1)+hi)p=zeros(1,length(x));%一维概率密度矩阵for xi=1:length(x) %概率密度网格遍历%根据parezen窗的叠函数求取概率密度Xi=x(xi)*ones(1,N(Ni));%Xi中心向量p(xi)=1/(sqrt(2*pi)*h(Ni,hi)*N(Ni))*sum(exp(-0.5*((X-Xi)/h(Ni,hi)).^2));endplot(x,p,'k-')   %估计的概率密度hold on plot(x,y,'r--')  %真实的概率密度title(['N=',num2str(N(Ni)),'  h1=',num2str(h1(hi))])end
end

效果图如下所示

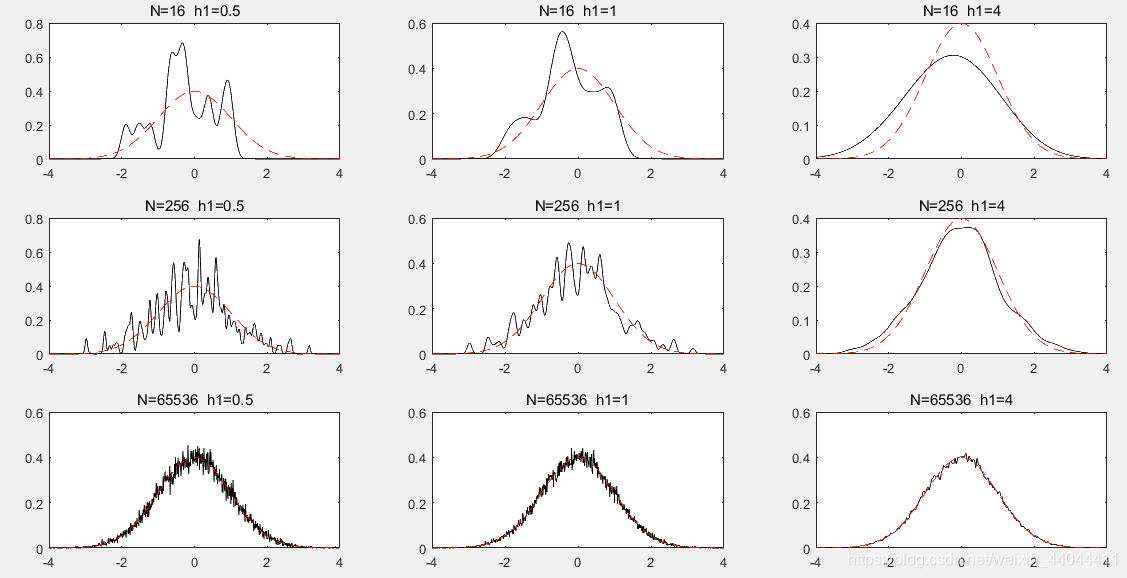
\qquad真实概率密度曲线用红色虚线表示，Parzen窗的估计概率密度用黑色实现表示，可以看出h=4时估计效果最好，随着样本数的增大，估计概率密度曲线逼近于真实概率密度曲线。事实上我们可以认为h标志着每个样本点的影响范围，h小的时候，样本点的影响范围小，但在小范围内的贡献率高；h大的时候样本点的影响范围大，在大范围内的贡献率会变小。当h大时，估计概率密度曲线会较为平滑，当h小时，估计概率密度曲线会较为尖锐。
\qquad但是这个h的选取并不是绝对的，就正态分布的样本而言，h的选择和方差有很大关系。试看下一个例子：其余参数均不变，样本服从$N(0,0.3)$的正态分布。

N=[2^4,2^8,2^16]';
x=-4:0.01:4;
y=1/(sqrt(2*pi)*0.3)*exp(-0.5*x.^2/0.09);
h1=[0.5,1,4];
h=h1./sqrt(N);
figure
for Ni=1:length(N) %按照指定样本数序列进行仿真X=normrnd(0,0.3,1,N(Ni));%生成指定数目特定分布的样本for hi=1:length(h1)  %取指定的h值subplot(length(N),length(h1),(Ni-1)*length(h1)+hi)p=zeros(1,length(x));%一维概率密度矩阵for xi=1:length(x) %概率密度网格遍历%根据parezen窗的叠函数求取概率密度Xi=x(xi)*ones(1,N(Ni));%Xi中心向量p(xi)=1/(sqrt(2*pi)*h(Ni,hi)*N(Ni))*sum(exp(-0.5*((X-Xi)/h(Ni,hi)).^2));endplot(x,p,'k-')   %估计的概率密度hold on plot(x,y,'r--')  %真实的概率密度title(['N=',num2str(N(Ni)),'  h1=',num2str(h1(hi))])end
end

效果图如下：

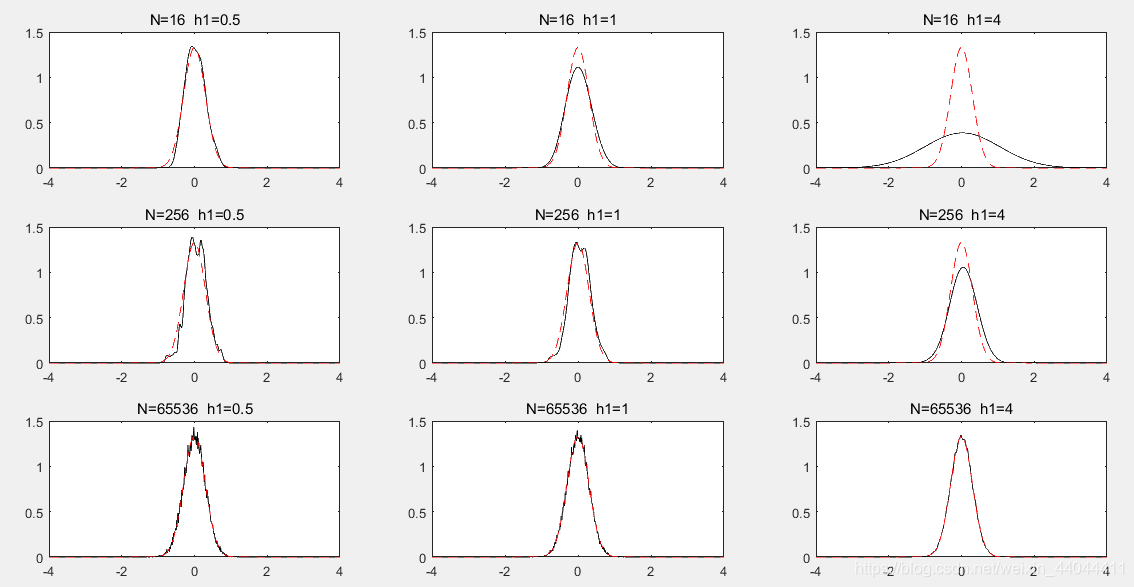
\qquad我们可以发现这一次，在N=16时，h=0.5的估计效果最好，h=4就显得过于平滑，均值附近不够集中；在N=256时，h=1的估计效果最好，h=0.5次之，h=4仍然是最差的，原因同上；在N=65536时，h=4的估计效果最好，因为样本数增多之后，h=4的估计仍然会收敛，而它的估计是最平滑的，因此毛刺最少，效果最好。由此可见，当方差较小、样本较少时，选取较小的h值具有优势，当方差较大、样本数较多时，选取较大的h值具有优势。

3.K近邻

3.1.算法原理

\qquad和Parzen窗法正好相反，Parzen窗法中体积V是样本数N的函数，而$K_N$近邻法中落入区域R的样本数$k$是N的函数。一般情况下，可以预先选定区域R包含的样本数$k$，然后不断增大体积，直到包含$k$个样本数为止。
\qquad我们规定$K_N=k\sqrt{N}$，k是邻近系数，k越大代表越多的样本点可以影响到观测点的概率密度，但每个样本点的影响也会降低。如何计算包含k个样本的最小体积呢？我们可以计算出离观测点最近的k个样本，这k个样本中离观测点最远的距离就是体积尺度s，最后所计算的概率密度为：
$$\hat{p}(x_0)=\frac{K_N}{2Ns}=\frac{k}{2\sqrt{N}s}$$
\qquad虽然这个表达式没有累加了，看起来比Parzen窗法复杂，实际上它的计算量毫不亚于Parzen窗法，原因在于每次计算观测点都需要对所有样本距离观测点的距离进行排序，排序需要消耗大量计算资源，若不采取改进措施，付出的时间代价和空间代价将是致命的。

3.2.Matlab实现与参数探究

\qquad同样，我们采用已知的$N(0,1)$分布样本对$K_N$近邻法进行测试，需要测试的参数仍然是样本数N和近邻系数$k$。选择$N=2^4,2^8,2^{16}$，选择$k=0.5,1,2$，这里需要额外注意的是$k\sqrt{N}<N$必须恒成立，否则会出现$K_N>N$的谬论，这个式子只需要在N取最小值的时候满足即可。

N=[2^4,2^8,2^16]';
x=-4:0.01:4;
k1=[0.5,1,2];
k=k1.*sqrt(N);
figure
for Ni=1:length(N) %按照指定样本数序列进行仿真X=normrnd(0,1,1,N(Ni));%生成指定数目特定分布的样本for ki=1:length(k1)  %取指定的h值subplot(length(N),length(k1),(Ni-1)*length(k1)+ki)p=zeros(1,length(x));%一维概率密度矩阵for xi=1:length(x) %概率密度网格遍历%根据parezen窗的叠函数求取概率密度Xi=x(xi)*ones(1,N(Ni));%Xi中心向量si=sort(abs(Xi-X));%对距离中心点的距离排序，排在第k个的时的距离为最小距离（体积）p(xi)=k(Ni,ki)/(N(Ni)*2*si(floor(k(Ni,ki))));%可能k不是整数，这里需要取整，因为排序只能是整数个排序endplot(x,p)title(['N=',num2str(N(Ni)),'  k1=',num2str(k1(ki))])end
end

效果图如下：

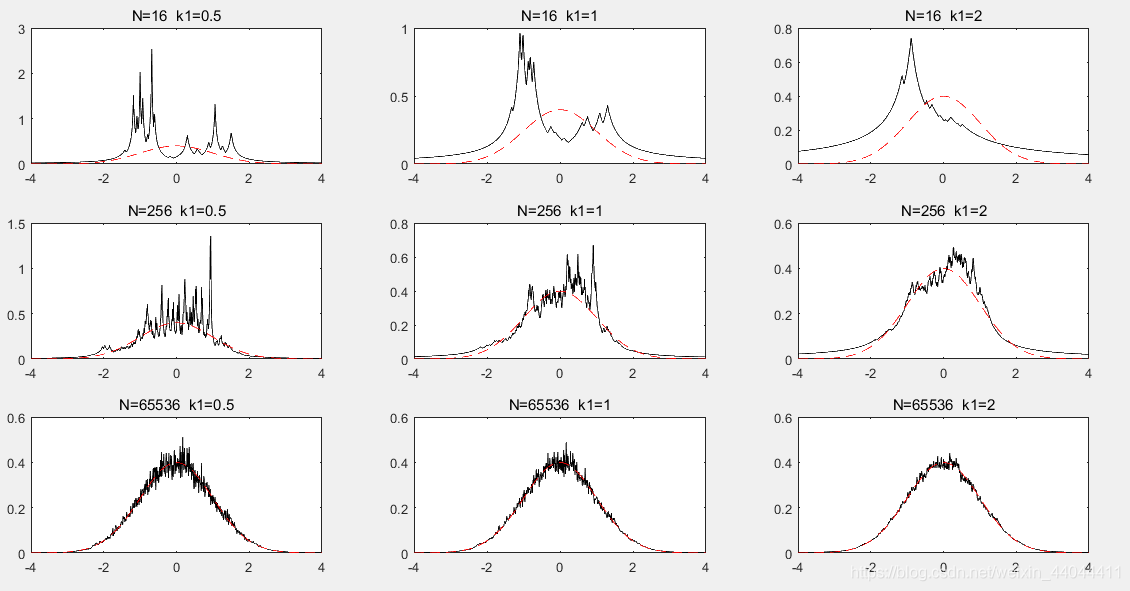
\qquad本次代码的运行时间大概是Parzen窗法的5~10倍左右，然而拟合效果远远不如Parzen窗法，即使是样本数最多，k值最合适的情况下，毛刺仍然相当多。其关键原因还是在于曲线不够平滑，说明单个观测点参考的数目还不够多，但是要增大k值，为了满足$k\sqrt{N}<N$，我们必须同时增大样本数。我们取样本数$N=2^{10},2^{12},2^{16}$,$k=5,10,20$再作观察：

N=[2^10,2^12,2^16]';
x=-4:0.01:4;
y=1/(sqrt(2*pi))*exp(-0.5*x.^2);
k1=[5,10,20];
k=k1.*sqrt(N);
figure
for Ni=1:length(N) %按照指定样本数序列进行仿真X=normrnd(0,1,1,N(Ni));%生成指定数目特定分布的样本for ki=1:length(k1)  %取指定的h值subplot(length(N),length(k1),(Ni-1)*length(k1)+ki)p=zeros(1,length(x));%一维概率密度矩阵for xi=1:length(x) %概率密度网格遍历%根据parezen窗的叠函数求取概率密度Xi=x(xi)*ones(1,N(Ni));%Xi中心向量si=sort(abs(Xi-X));%对距离中心点的距离排序，排在第k个的时的距离为最小距离（体积）p(xi)=k(Ni,ki)/(N(Ni)*2*si(floor(k(Ni,ki))));%可能k不是整数，这里需要取整，因为排序只能是整数个排序endplot(x,p,'k-') %估计概率密度hold onplot(x,y,'r--') %真实概率密度title(['N=',num2str(N(Ni)),'  k1=',num2str(k1(ki))])end
end

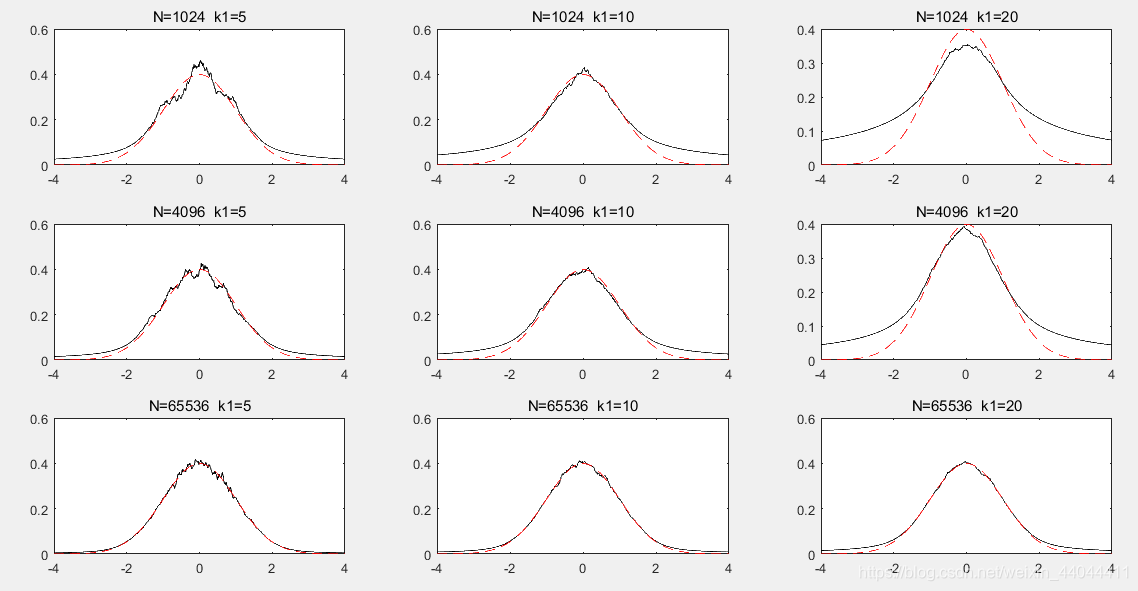
可以发现，现在的拟合效果比刚刚要好很多，可以和Parzen窗法的拟合相媲美了，但是算法运算速度上仍然要慢，原因还是在于排序法拖慢了运算速度，其算法复杂度和样本数是成平方关系的。
我们再来让K近邻法估计一组服从$N(0,0.09)$的样本作比较，其效果图如下：

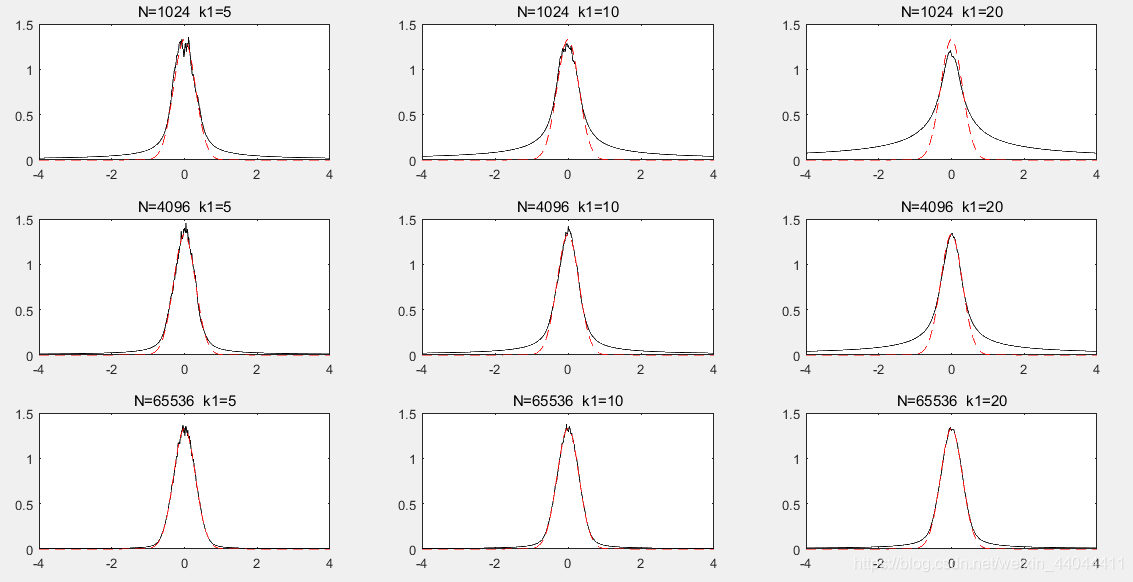
\qquad通过上图我们也可看出k值选取和样本数和方差也是有关系的，有意思的是，在方差为1时，$N=2^{10}$和$N=2^{12}$的情况下都是k=10比较好，$N=2^{16}$时k=20比较好。然而当方差为0.09时，随着N的增大，k=5几乎总是最好的。然而k=10和k=20随着样本数的增大，逼近程度也在增加，考虑到k值越大曲线越平滑，因此选择k值也是需要在方差和样本数之间做权衡的。
\qquad最后感谢您的阅读，希望本文对您有帮助！