文章目录
- 0.聚类分析简介
- 0.1.简单的聚类样本生成器
- 1.静态聚类算法
- 1.1.最近邻聚类算法
- 1.1.1.算法原理
- 1.1.2.参考代码
- 1.1.3.参数选择及运行结果
- 1.2.最大最小距离法
- 1.2.1.算法原理
- 1.2.2.参考代码
- 1.2.3.参数选择及运行结果
- 2.动态聚类算法
- 2.1.C均值聚类算法
- 2.1.1.算法原理
- 2.1.2.参考代码
- 2.1.3.运行效果
- 2.2.不需要类别参数的C均值聚类算法
- 2.2.1.算法原理
- 2.2.2.参考代码
- 2.2.3.运行结果
0.聚类分析简介
\qquad模式识别有两个重要的分支——分类算法和聚类算法。分类算法依赖于已知类别的样本,对未知的样本进行分类,是一种监督学习的算法;聚类算法是利用样本的分布特征,将样本按照一定规则划分为几个聚类,从而达到分类的目的,是一种非监督学习算法(有些聚类算法并不是完全的非监督),本文介绍的就是聚类算法。
0.1.简单的聚类样本生成器
\qquad在实现我们的聚类算法之前,我们需要生成我们需要的样本,聚类算法不像分类算法一样有线性可分与非线性可分的区分,但生成的样本适不适合做聚类算法,也和类别与类别直接的聚类中心以及聚类域半径有关。
\qquad我们的思路是先确定类别数和每个类别的聚类中心坐标、聚类域最大半径。然后在聚类中心周围随机生成样本,最后将所有样本的顺序打乱,就可以作为我们聚类算法的样本了。
\qquad本人书写的一个参考程序如下:(目前只支持2维样本)
n=input('请输入需要生成的类别数n:\n');%样本类别
N=input('请输入每个类别样本数组成的行矩阵N:\n');%每个类别的样本数
if numel(N)~=nerror('矩阵N维度必须等于类别数n!:\n')
end
C=input('请输入各类的聚类中心(按行输入)矩阵C:\n');%x为样本中心矩阵,每列为一个聚类中心
if size(C,1)~=nerror('C矩阵格式错误!')
end
R=input('请输入每类样本的最大半径行矩阵R:\n');
if numel(R)~=nerror('矩阵R维度必须等于类别数n!')
end
X=zeros(sum(N),2);%样本总矩阵
k=1;
for i=1:nr=R(i)*rand(N(i),1);theta=2*pi*rand(N(i),1);X(k:k+N(i)-1,:)=[C(i,1)*ones(N(i),1)+r.*cos(theta),C(i,2)*ones(N(i),1)+r.*sin(theta)];k=k+N(i);
end
plot(X(:,1),X(:,2),'*')
以下是一个生成案例:

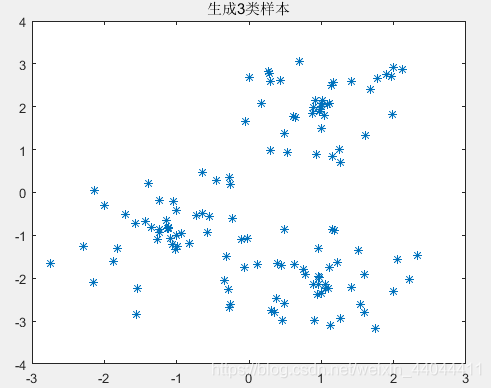
生成的样本如下图所示:
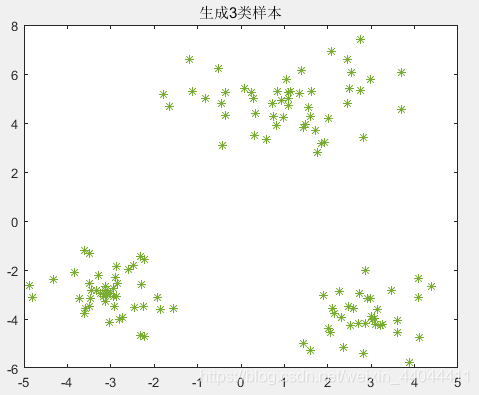
\qquad可以发现,随机分布的样本具有一定的规律性,第一类和第三类的半径差不多,第二类的聚类域半径较大,三个聚类的聚类中心相互之间都有足够的距离。下面我们就借助这个聚类样本生成器完成以下的实验。
1.静态聚类算法
\qquad静态聚类算法中,一个样本的归属一旦确定后,在后续的迭代过程中不再不发生变化,而动态聚类算法则会根据聚类准则函数的误差平方和最小的原则,随时调整样本的归属以达到最优。
1.1.最近邻聚类算法
1.1.1.算法原理
\qquad最近邻聚类算法又称为最小距离的聚类算法,其原理是先选定一个分类阈值,不断地抽取样本,判断它与上一个样本的距离,若小于阈值则归为一类,否则将其定义为新的聚类中心。算法步骤如下:
- 选定距离阈值TTT,设样本数为NNN,转第2步
- 将第一个样本x1x_1x1设定为第一个聚类中心C1C_1C1,样本计数器i=1i=1i=1,类别计数器m=1m=1m=1,转第3步
- 依次计算第i+1i+1i+1个样本xi+1x_{i+1}xi+1与前mmm个类别的聚类中心C1,C2,...,CmC_1,C_2,...,C_mC1,C2,...,Cm距离d1,d2,...,dmd_1,d_2,...,d_md1,d2,...,dm,若存在1≤j≤m1≤j≤m1≤j≤m使得dj<Td_j<Tdj<T,则将xi+1x_{i+1}xi+1归为第jjj类,否则,产生新的第m+1m+1m+1类,并将xi+1x_{i+1}xi+1定义为聚类中心Cm+1C_{m+1}Cm+1,m=m+1m=m+1m=m+1。转第4步
- 计数器i=i+1i=i+1i=i+1,若i<Ni<Ni<N则转第3步,否则终止。
1.1.2.参考代码
参考代码如下:
function Y=nearest(X,T)
%最近邻规则聚类,Y是X样本的分类标号,T为距离阈值
n=size(X,1);
Y=ones(n,1);%分类标号
class_n=1;%类别数
x0=X(1,:);%第一个聚类中心
center=x0;%center矩阵存放聚类中心
for i=1:n-1x1=X(i+1,:);isnew=true;for j=1:class_nif normest(x1-center(j,:))<TY(i+1)=j;isnew=false;breakendendif isnewclass_n=class_n+1;%类别数+1center(size(center,1)+1,:)=x1;%新的聚类中心Y(i+1)=class_n;%归为新的一类end
end
for c=1:class_nplot(X(Y==c,1),X(Y==c,2),'*')hold on
end
title(['最近邻法-距离阈值:',num2str(T),' 分为:',num2str(class_n),'类'])1.1.3.参数选择及运行结果
现在需要选定距离阈值的参数,我计算三个聚类中心之间的距离如下:

\qquad而样本在同类中的最大间距为6(第二类样本最大半径的2倍),选择的阈值过大会把不同类的样本划分为同一类,选择的阈值太小则会在同类样本中再进行划分,产生不必要的多余类,在这里我们需要选择一个4.3~6之间的数作为阈值,作者选择的是4.5。分类情况如下:
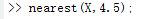
\qquad如果距离阈值选择的不合适,或者样本的顺序不适合使用最近邻分类法,那么可能会出现分类错误的情况。如下图所示:
| 距离阈值 | 4 | 6 |
|---|---|---|
| 分类结果 |  |  |
\qquad可以发现选择的阈值过大会把不同类的样本划分为同一类,选择的阈值太小则会在同类样本中再进行划分,产生不必要的多余类。
1.2.最大最小距离法
1.2.1.算法原理
\qquad最大最小距离法除了首先辨识最远的聚类中心外,其余方法和最近法相类似,它的算法步骤如下:
- 给定θ\thetaθ,0<θ<10<\theta<10<θ<1,任取一个样本作为第一个聚类中心C1C_1C1,转步2。
- 计算所有的样本到C1C_1C1的距离,并将距离最远的一个样本最为第二个聚类中心C2C_2C2,设C1,C2C_1,C_2C1,C2之间的距离为z1z2z_1z_2z1z2,类别数m=2。
- 计算每个样本xix_ixi到各个聚类中心的距离Di1,Di2,....,DimD_{i1},D_{i2},....,D_{im}Di1,Di2,....,Dim并取每个样本的最小距离Di=min{Di1,Di2,...,Dim}D_i=min\lbrace D_{i1},D_{i2},...,D_{im}\rbraceDi=min{Di1,Di2,...,Dim},选出每个样本最小距离中的最大值D=max{Di}D=max\lbrace D_i \rbraceD=max{Di},转步4
- 若D>θz1z2D>\theta z_1z_2D>θz1z2,则在最小距离DiD_iDi中最大的那个样本处产生新的聚类中心Cm+1C_{m+1}Cm+1,m=m+1m=m+1m=m+1,转步3;若D≤θz1z2D≤\theta z_1z_2D≤θz1z2,则不再产生新的聚类中心,转步5。
- 按照最近邻法进行分类,对于每个样本xix_ixi,它距离哪个聚类中心最近则归为哪一类。
1.2.2.参考代码
\qquad我们仍然借助我们的聚类样本生成器产生的样本进行测试,参考代码如下:
function Y=max_min(X,theta)
%最大最小规则聚类,Y是X样本的分类标号,theta为距离阈值系数
n=size(X,1);%n是样本数
class_n=2;%类别数
x0=X(1,:);%第一个聚类中心
d=@(x)(sum(abs(ones(n,1)*x-X).^2,2).^(1/2));%距离函数
[~,max_i]=max(d(x0));%求出最大距离D12并产生第2个聚类中心
x1=X(max_i,:);%第二个聚类中心
center=[x0;x1];%聚类中心矩阵更改
T=normest(x0-x1)*theta;%聚类中心产生阈值
[D,max_i]=max(min(cat(2,d(x0),d(x1)),[],2));%最大最小距离
%step1 确定聚类中心
cat_d=cat(2,d(x0),d(x1));%Di1和Di2
while D>T %聚类中心class_n=class_n+1;center(class_n,:)=X(max_i,:);cat_d=cat(2,cat_d,d(center(class_n,:)));[D,max_i]=max(min(cat_d,[],2));
end
%step2 分类
[~,Y]=min(cat_d,[],2);
for c=1:class_nplot(X(Y==c,1),X(Y==c,2),'*')hold on
end
title(['最大最小距离法-距离系数:',num2str(theta),' 分为:',num2str(class_n),'类'])1.2.3.参数选择及运行结果
\qquad由于三类样本的聚类中心间距分别为4.2426,4.2426,5.0990,聚类域半径为2,2,3。24.2426=0.4714\frac{2}{4.2426}=0.47144.24262=0.4714,4.24265=0.832\frac{4.2426}{5}=0.83254.2426=0.832,所以选择的0.4714<θ<0.8320.4714<\theta<0.8320.4714<θ<0.832。如果选择的θ\thetaθ过小,可能会出现多分类的情况;反之,若θ\thetaθ选择过大,可能最终只有2类。根据最大最小距离法的算法原理我们可以知道,在选择聚类中心时,每选择一个,产生的“最大最小距离”都比之前的小。但和最近邻聚类算法相比,最大最小距离法的参数敏感性并不是特别强,在这里笔者选择的θ=0.6\theta=0.6θ=0.6。
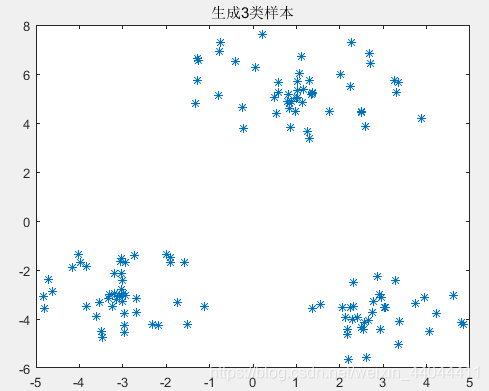
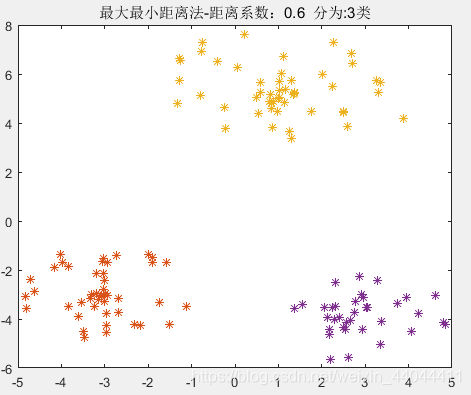
为了验证这种算法的参数敏感性,我们选择多个θ\thetaθ查看效果:
| θ=0.3\theta=0.3θ=0.3 | θ=0.4\theta=0.4θ=0.4 | θ=0.5\theta=0.5θ=0.5 |
|---|---|---|
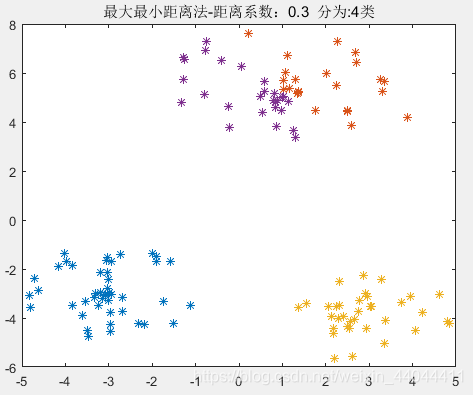 |  | 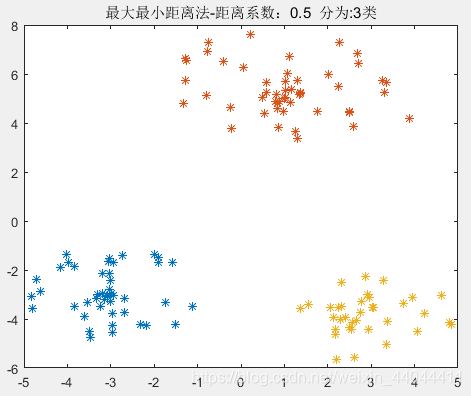 |
| θ=0.7\theta=0.7θ=0.7 | θ=0.75\theta=0.75θ=0.75 | θ=0.8\theta=0.8θ=0.8 |
| – | – | – |
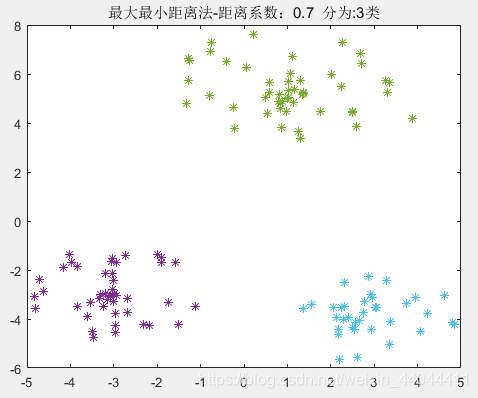 |  | 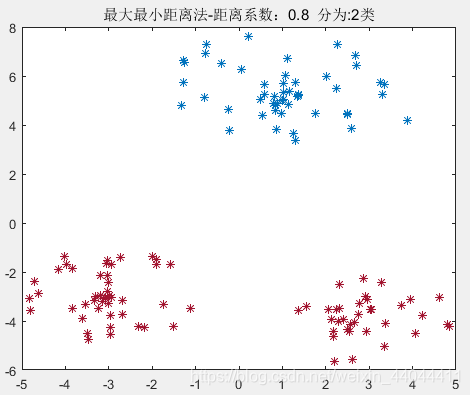 |
由此可见,0.4<θ<0.750.4<\theta<0.750.4<θ<0.75均可以得到完全正确的分类结果,这就验证了我们上述的理论。
2.动态聚类算法
\qquad和静态聚类算法不同,动态聚类算法回正迭代过程中不断调整样本的归属,以满足误差平方和准则。在介绍误差平方和准则Jc=∑j=1c∑k=1Nj∣∣Xk(j)−mj∣∣2J_c=\sum_{j=1}^{c}\sum_{k=1}^{N_j}||X_k^{(j)}-m_j||^2Jc=j=1∑ck=1∑Nj∣∣Xk(j)−mj∣∣2
\qquad式中NjN_jNj为第jjj类样本数,mjm_jmj为第jjj类ωj\omega_jωj的均值。Xk(j)X_k^{(j)}Xk(j)为第jjj类样本的第kkk个样本。可以看出,内部求和符号反映了同一类中样本的聚集程度,外层求和符号是对每类样本的方差求和,反映了样本整体的聚集程度。JcJ_cJc越大,聚集程度越小,反之越大。
2.1.C均值聚类算法
2.1.1.算法原理
III为迭代次数,Zj(I)Z_j(I)Zj(I)为第III次迭代的第jjj个聚类中心,XkX_kXk为第kkk个样本
- 首先确定需要分类的个数c,从N个样本{X1,X2,...,XN}\lbrace X_1,X_2,...,X_N\rbrace{X1,X2,...,XN}中选取c个任意样本作为初始聚类中心Z1(1),Z2(1),...,Z3(1)。Z_1(1),Z_2(1),...,Z_3(1)。Z1(1),Z2(1),...,Z3(1)。
- 计算每个样本到聚类中心的距离D(Xk,Zj(I)),k=1,2,...,n,j=1,2,...,cD(X_k,Z_j(I)),k=1,2,...,n,j=1,2,...,cD(Xk,Zj(I)),k=1,2,...,n,j=1,2,...,c。若D(Xk(j),Zj(I))=min{D(Xk,Z1(I)),D(Xk,Z2(I)),...,D(Xk,Zc(I))},k=1,2,...,nD(X_k^{(j)},Z_j(I))=min\lbrace D(X_k,Z_1(I)) ,D(X_k,Z_2(I)) ,...,D(X_k,Z_c(I))\rbrace,k=1,2,...,nD(Xk(j),Zj(I))=min{D(Xk,Z1(I)),D(Xk,Z2(I)),...,D(Xk,Zc(I))},k=1,2,...,n,则Xk∈ωjX_k∈\omega_jXk∈ωj。这一步就是利用最近邻法对样本进行分类
- 求出新的聚类中心Zj(I+1)=1Nj∑k=1NjXk(j),j=1,2,...,cZ_j(I+1)=\frac{1}{N_j}\sum_{k=1}^{N_j}X_k^{(j)},j=1,2,...,cZj(I+1)=Nj1k=1∑NjXk(j),j=1,2,...,c
- 若Zj(I+1)≠Zj(I),j=1,2,...,cZ_j(I+1)≠Z_j(I),j=1,2,...,cZj(I+1)=Zj(I),j=1,2,...,c则I=I+1I=I+1I=I+1,返回(2),否则算法结束。
\qquad这个算法看起来并不复杂,但是需要事先制定要分类的类别数,无法工作在完全无监督的环境下。但是,我们也可以使用最大最小距离法中产生聚类中心的方法去初始化C均值算法的类别数c和初始聚类中心。
2.1.2.参考代码
function Y=C_mean(X,c)
%Y是最终分类标号,X是样本矩阵,c是预分类类别数
n=size(X,1);%样本数
C=X(1:c,:);%聚类中心
new_C=zeros(c,2);%下一次迭代的聚类中心
d=@(x)(sum(abs(ones(n,1)*x-X).^2,2).^(1/2));%距离函数
cat_d=zeros(n,c);%距离矩阵,每行是每个样本到各个聚合中心的距离
for i=1:ccat_d(:,i)=d(C(i,:));
end
[~,Y]=min(cat_d,[],2);
for i=1:cnew_C(i,:)=mean(X(Y==i,:));%修正聚类中心
end
t=1;%迭代次数记录
while new_C~=C%标定聚类中心位置figure(t)plot(C(:,1),C(:,2),'o','MarkerSize',10,'MarkerEdgeColor','b')hold onfor i=1:cplot(X(Y==i,1),X(Y==i,2),'*')hold onendtitle(['C均值法-分类数:',num2str(c),' 迭代次数为:',num2str(t),'次'])t=t+1;%迭代次数+1C=new_C; %更新聚类中心位置for i=1:ccat_d(:,i)=d(C(i,:));end[~,Y]=min(cat_d,[],2);for i=1:cnew_C(i,:)=mean(X(Y==i,:));%修正聚类中心end
end
figure(t)
plot(C(:,1),C(:,2),'o','MarkerSize',10,'MarkerEdgeColor','b')
hold on
for i=1:cplot(X(Y==i,1),X(Y==i,2),'*')hold on
end
title(['C均值法-分类数:',num2str(c),' 迭代次数为:',num2str(t),'次'])
\qquad注意,在【算法原理】的第一步,随机选取样本作为聚类中心,我们直接指定了样本的前3个作为3个聚类中心,随机指定当然也是可以的。
2.1.3.运行效果
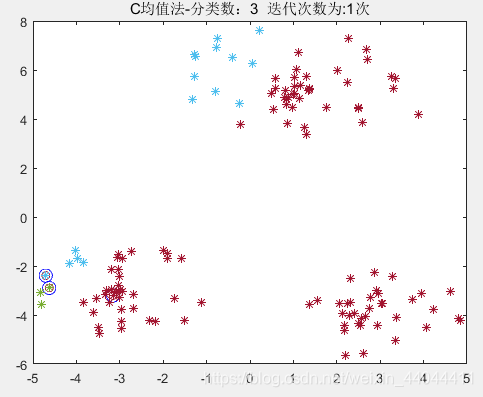

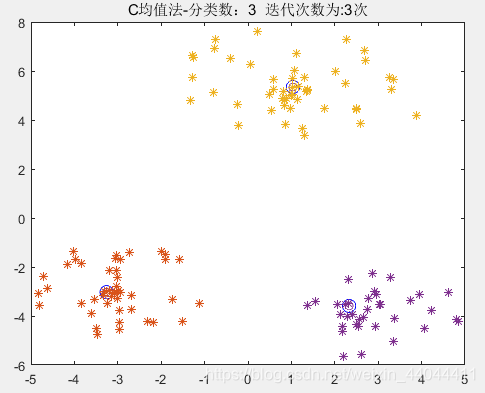
\qquad这需要事先指定的参数只有分类数ccc,如果ccc是已知的,则C均值聚类算法则不需要任何参数,和其余静态聚类算法相比不存在参数敏感性问题。但是这也是它的缺陷之一,即必须事先指定分类数ccc。
2.2.不需要类别参数的C均值聚类算法
2.2.1.算法原理
\qquad如果使用最大最小距离法事先确定ccc,则不需要事先制定类别数,但需要事先指定系数θ\thetaθ,选择θ\thetaθ的方法可以参考1.2节的最大最小距离法。在这里我们只需要模仿最大最小距离法写一个分类程序,再将初始化的聚类中心和分类数用于C均值聚类即可。
2.2.2.参考代码
function Y=C_mean(X,theta)
%% 确定类别数class_n
%Y是最终分类标号,X是样本矩阵,c是预分类类别数
n=size(X,1);%n是样本数
class_n=2;%类别数
x0=X(1,:);%第一个聚类中心
d=@(x)(sum(abs(ones(n,1)*x-X).^2,2).^(1/2));%距离函数
[~,max_i]=max(d(x0));%求出最大距离D12并产生第2个聚类中心
x1=X(max_i,:);%第二个聚类中心
C=[x0;x1];%聚类中心矩阵更改
T=normest(x0-x1)*theta;%聚类中心产生阈值
[D,max_i]=max(min(cat(2,d(x0),d(x1)),[],2));%最大最小距离
%step1 确定聚类中心
cat_d=cat(2,d(x0),d(x1));%Di1和Di2
while D>T %聚类中心class_n=class_n+1;C(class_n,:)=X(max_i,:);cat_d=cat(2,cat_d,d(C(class_n,:)));[D,max_i]=max(min(cat_d,[],2));
end
[~,Y]=min(cat_d,[],2);%最近邻分类
new_C=zeros(class_n,2);%下一次迭代的聚类中心
for i=1:class_nnew_C(i,:)=mean(X(Y==i,:));%修正聚类中心
end
t=1;%迭代次数记录
%% 在已有类别数基础上进行C均值分类
while new_C~=C%标定聚类中心位置figure(t)plot(C(:,1),C(:,2),'o','MarkerSize',10,'MarkerEdgeColor','b')hold onfor i=1:class_nplot(X(Y==i,1),X(Y==i,2),'*')hold onendtitle(['C均值法-分类数:',num2str(class_n),' 迭代次数为:',num2str(t),'次'])t=t+1;%迭代次数+1C=new_C; %更新聚类中心位置for i=1:class_ncat_d(:,i)=d(C(i,:));end[~,Y]=min(cat_d,[],2);for i=1:class_nnew_C(i,:)=mean(X(Y==i,:));%修正聚类中心end
end
figure(t)
plot(C(:,1),C(:,2),'o','MarkerSize',10,'MarkerEdgeColor','b')
hold on
for i=1:class_nplot(X(Y==i,1),X(Y==i,2),'*')hold on
end
title(['C均值法-分类数:',num2str(class_n),' 迭代次数为:',num2str(t),'次'])
\qquad由于样本之间相隔较远,使用最大最小距离法就已经得到了正确的分类结果,C均值只是修正了一下聚类中心的位置,因此我们可以对比一下样本类之间距离较近时,单纯的最大最小距离法和最大最小距离法+C均值聚类的区别。
\qquad初始化聚类生成引擎,参数设置如下:

2.2.3.运行结果
选取θ=0.6\theta=0.6θ=0.6,运行上述代码,即可得到如下结果:
\qquad由于样本之间相隔较远,使用最大最小距离法就已经得到了正确的分类结果,C均值只是修正了一下聚类中心的位置,因此我们可以对比一下样本类之间距离较近时,单纯的最大最小距离法和最大最小距离法+C均值聚类的区别。

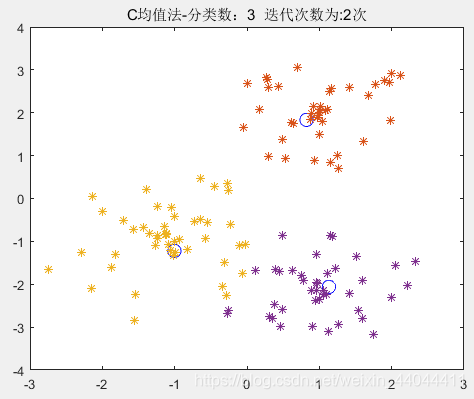
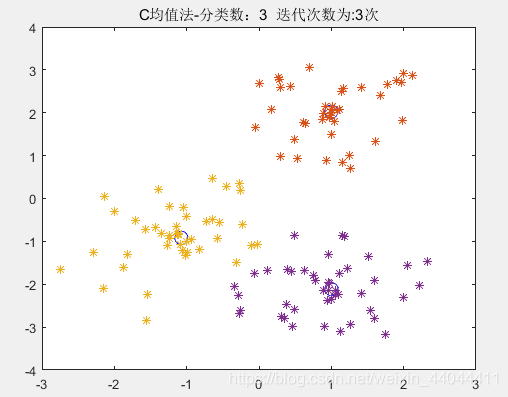
\qquad单纯的最大最小距离法的分类结果就是第一幅图,而最大最小距离法+C均值聚类则可以达到图3的效果。我们定量的比较一下误差平方和函数JcJ_cJc随着迭代次数的变化:
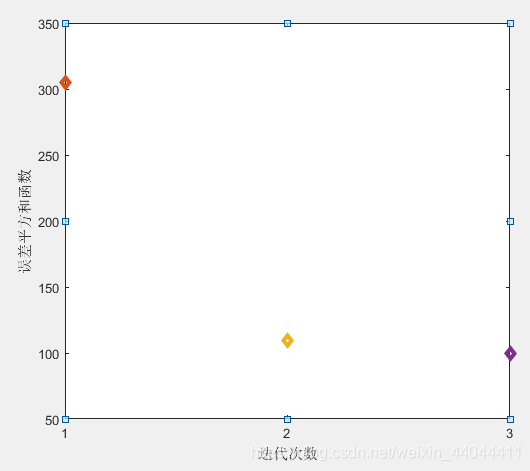
\qquad可以发现,单纯的最大最小距离法的JcJ_cJc有300多(即第一次的迭代结果),而最大最小距离法+C均值聚类分析的JcJ_cJc经过了3次迭代修正,JcJ_cJc已经下降至了小于100,因此后者具有更优的分类效果。
希望本文对您有帮助,感谢您的阅读!

)




)
:I/O操作)


【运动学轨迹规划】)



简易教程)




