灰度共生矩阵及其数字特征_数字系统及其表示

灰度共生矩阵及其数字特征

Any number system has a set of symbols known as Digits with some rules performing arithmetic operations. A collection of these makes a number has two parts. They are integer portion and fraction portion. These portions are separated by a point known as radix.

任何数字系统都有一组称为数字的符号，其中某些规则执行算术运算。这些的集合使数字分为两个部分。它们是整数部分和小数部分 。这些部分被称为radix的点隔开。

If a number has radix as 'b', then the number of numbers present in that number system will be 'b' which will range from 0 to b-1.

如果一个数字的基数为'b' ，则该数字系统中存在的数字数将为'b' ，范围从0到b-1 。

Where,

哪里，

N = a number
N =一个数字
b = radix or base to number system
b =基数或基数系统
n = number of digits in integer portion
n =整数部分的位数
m = number of digits in the fractional portion
m =小数部分的位数
d_n-1 = Most Significant Digit (MSD)
d _n-1 =最高有效位(MSD)
d_-m = Least Significant Digit (LSD)
d _-m =最低有效位(LSD)

The commonly used number systems are:

常用的数字系统是：

Binary Number System
二进制数制
Octal Number System
八进制数字系统
Decimal Number System
小数系统
Hexadecimal Number System
十六进制数制

1)二进制数制 (1) Binary Number System)

The binary number system has its base as 2. Since b=2, it consists of two digits which range from 0 to 2-1 =1. (As discussed above, the range is from 0 to b-1).

二进制数字系统的底数为2 。由于b = 2 ，它由两位数字组成，范围从0到2-1 = 1 。 (如上所述，范围是从0到b-1 )。

Therefore, the binary number system consists of digits 0 and 1 only.

因此， 二进制数字系统仅由数字0和1组成。

Ex: (1101)2, (110101)2, (0101)2, (101.01)2, etc.

例如：(1101)2，(110101)2，(0101)2，(101.01)2等。

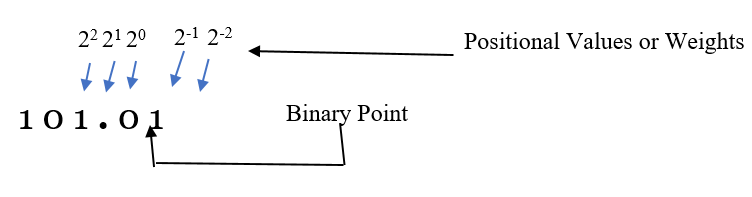
In Binary Number System, the portion to the left of binary point (integer part) have their weights as 2⁰, 2¹, 2² and so on from right to left. The portion on the right-hand side of the binary point (fractional part) have weights as 2^-1, 2^-2 and so on from left to right.

在二进制数字系统 ，该部分向左侧二进制点(整数部分)具有它们的权重为2 ^0，2 ^1，2 ²等从右到左。二元点右侧的部分(分数部分)的权重从左到右依次为2 ^-1，2 ^-2 ，依此类推。

Above given binary number (101.01)₂ can be represented as:

上面给出的二进制数(101.01) ₂可以表示为：

(101.01)₂ = (1*2²) + (0*2¹) + (1*2⁰) + (0*2^-1) + (1*2^-2)

(101.01) ₂ =(1 * 2 ² )+(0 * 2 ¹ )+(1 * 2 ⁰ )+(0 * 2 ^-1 )+(1 * 2 ^-2 )

After simplifying the terms in the RHS of the equation, we will get a decimal number equivalent to binary number on the LHS which is (5.25)₁₀.

简化方程式RHS中的项后，我们将得到一个与LHS上的二进制数等效的十进制数(5.25) ₁₀ 。

2)八进制数字系统 (2) Octal Number System)

The octal number system has its base as 8. Since b=8, it consists of eight digits which range from 0 to 8-1 =7. (As discussed above, the range is from 0 to b-1).

八进制数制的底数为8 。由于b = 8 ，因此它由八位数字组成，范围从0到8-1 = 7 。 (如上所述，范围是从0到b-1 )。

It consists of digits ranging from 0 to 7 i.e., 0, 1, 2, 3, 4, 5, 6 and 7.

它由0到7之间的数字组成，即0、1、2、3、4、5、6和7 。

Ex: (73)8, (420)8, (125.13)8, etc.

例如：(73)8，(420)8，(125.13)8等

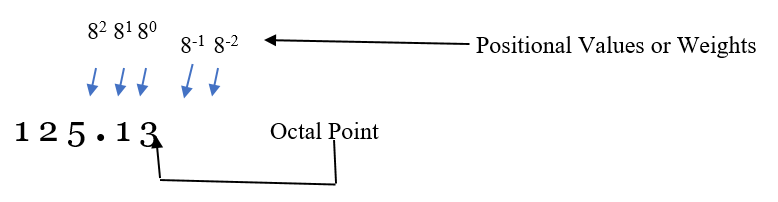
In Octal Number System the positional values/weights to the left of octal point in integer part are as 8⁰, 8¹, 8² and so on from right to left whereas the weights in the right-hand side in fractional part are as 8^-1, 8^-2 and so on from left to right.

在八进制数系统的位置值/权重为八进制点的左侧在整数部分是作为8 ^0，8 ^1，8 ²等从右到左，而在小数部分的右手侧上的权重是作为8 ^-1，8 ^-2等等，从左到右。

Above given octal number (125.13)₈ can be represented as:

上面给出的八进制数(125.13) ₈可以表示为：

(125.13)₈ = (1*8²) + (2*8¹) + (5*8⁰) + (1*8^-1) + (3*8^-2)

(125.13) ₈ =(1 * 8 ² )+(2 * 8 ¹ )+(5 * 8 ⁰ )+(1 * 8 ^-1 )+(3 * 8 ^-2 )

After simplifying the terms in the RHS of the equation, we will get a decimal number equivalent to octal number on the LHS which is (85.140625)₁₀.

简化方程式RHS中的项后，我们将得到一个与LHS上的八进制数等效的十进制数，即(85.140625) ₁₀ 。

小数系统 (Decimal Number System)

The Decimal Number System has its base as 10. Since b=10, it consists of 10 digits which range from 0 to 10-1 = 9. (As discussed above, the range is from 0 to b-1).

小数系统的底数为10 。由于b = 10 ，因此它由10个数字组成，范围从0到10-1 = 9 。 (如上所述，范围是从0到b-1 )。

It consists of digits ranging from 0 to 9 i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.

它由0到9之间的数字组成，即0、1、2、3、4、5、6、7、8和9 。

Ex: (101)10, (12)10, (999)10, (540.25)10, etc.

例如：(101)10，(12)10，(999)10，(540.25)10等

In the Decimal Number System the positional values/weights to the left of the decimal point in integer part are as 10⁰, 10¹, 10² and so on from right to left whereas the weights in the right-hand side in fractional part are as 10^-1, 10^-2 and so on from left to right.

在十进制系统的位置值/权重到小数点的左边在整数部分是为10 ^0，10 ^1，10 ²等从右到左，而在小数部分是在右手侧的权重从左到右依次为10 ^-1，10 ^-2等。

Above given decimal number (540.25)₁₀ can be represented as:

高于给定的十进制数(540.25) ₁₀可以表示为：

(540.25)₁₀ = (5*10²) + (4*10¹) + (0*10⁰) + (2*10^-1) + (5*10^-2)

(540.25) ₁₀ =(5 * 10 ² )+(4 * 10 ¹ )+(0 * 10 ⁰ )+(2 * 10 ^-1 )+(5 * 10 ^-2 )

After simplifying the terms in the RHS of the equation, we will get a decimal number equivalent to the decimal number on the LHS.

简化方程式RHS中的项后，我们将得到一个与LHS上的十进制数等效的十进制数。

4)十六进制数制 (4) Hexadecimal Number System)

The Hexadecimal Number System has its base as 16. Since b=16, it consists of 16 digits which range from 0 to 16-1 = 15. (As discussed above, the range is from 0 to b-1).

十六进制数字系统的底数为16 。由于b = 16 ，它由16位数字组成，范围从0到16-1 = 15 。 (如上所述，范围是从0到b-1 )。

It consists of both digits and alphabets where digits range from 0 to 9 i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and alphabets range from A to F where (A=10), (B=11), (C=12), (D=13), (E=14) and (F=15).

它由数字和字母组成，其中数字范围从0到9，即0、1、2、3、4、5、6、7、8、9，字母范围从A到F ，其中( A = 10) ， ( B ＝ 11) ，( C ＝ 12 )，( D ＝ 13 )，( E ＝ 14 )和( F ＝ 15 )。

Ex: (123)16, (459)16, (12A3F.12)16, etc.

例如：(123)16，(459)16，(12A3F.12)16等。

In the Hexadecimal Number System the positional values/weights to the left of the decimal point in integer part are as 16⁰, 16¹, 16² and so on from right to left whereas the weights in the right-hand side in fractional part are as 16^-1, 16^-2 and so on from left to right.

在十六进制数系统的位置值/权重到小数点的左边在整数部分是为16 ^0，16 ^1，16 ²等从右到左，而在小数部分是在右手侧的权重从左到右依次为16 ^-1，16 ^-2等。

Above given Hexadecimal number (12A.13)₁₆ can be represented as:

上面给出的十六进制数(12A.13) ₁₆可以表示为：

(12A.13)₁₆ = (1*16²) + (2*16¹) + (10*16⁰) + (1*16^-1) + (3*16^-2)

(12A.13) ₁₆ =(1 * 16 ² )+(2 * 16 ¹ )+(10 * 16 ⁰ )+(1 * 16 ^-1 )+(3 * 16 ^-2 )

After simplifying the terms in the RHS of the equation, we will get a decimal number equivalent to decimal number on the LHS which is (298. 06640625)₁₀.

简化方程式RHS中的项后，我们将得到一个与LHS上的十进制数相等的十进制数，即(298. 06640625) ₁₀ 。