olap 多维分析
In the previous article of OLAP, we have seen various applications of OLAP, Various types of OLAP, advantages, and disadvantages of OLAP. In this article, we will learn about the,
在OLAP的上一篇文章中,我们了解了OLAP的各种应用,各种类型的OLAP,OLAP的优缺点 。 在本文中,我们将了解
OLAP Cube
OLAP多维数据集
OLAP Cube Operations
OLAP多维数据集操作
1)OLAP多维数据集 (1) OLAP Cube)
An OLAP cube may be a multi-dimensional array of knowledge. The online analytical process (OLAP) may be a computer-based technique of analyzing knowledge to appear for insights. The term cube here refers to a multi-dimensional dataset, that is additionally known as a Hypercube if the quantity of dimensions is larger than three. A cube is also thought of as a multi-dimensional generalization of a two- or three-dimensional program. For instance, a corporation may like to summarize monetary knowledge by product, by time-period, and by the town to check actual and budget expenses. Product, time, cities and situation (actual and budget) are the data's dimensions as shown in the figure. A cube isn't a "cube" within the strict mathematical sense, as all the edges aren't essentially equal.
OLAP多维数据集可以是知识的多维数组。 在线分析过程(OLAP)可能是一种基于计算机的技术,用于分析知识以获取见解。 术语“多维数据集”在这里是指多维数据集,如果维的数量大于3,则又称为“超多维数据集”。 多维数据集也被认为是二维或三维程序的多维概括。 例如,公司可能希望按产品,时间段和镇来汇总货币知识,以检查实际和预算支出。 产品,时间,城市和情况(实际和预算)是数据的尺寸,如图所示。 在严格的数学意义上,多维数据集不是“多维数据集”,因为所有的边实际上都不相等。
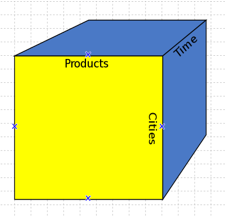
Fig 1: OLAP Cube
图1:OLAP多维数据集
2)OLAP多维数据集操作 (2) OLAP Cube Operations)
Since OLAP servers work on data of multidimensional view, we are going to discuss OLAP operations in multidimensional information.
由于OLAP服务器可以处理多维视图的数据,因此我们将在多维信息中讨论OLAP操作。
Here is the list of OLAP operations,
这是OLAP操作的列表,
Roll-up
卷起
Drill-down
下钻
Slice
片
Dice
骰子
Pivot (rotate)
枢轴旋转
2.1。 卷起 (2.1. ROLL UP)
Roll-up is performed by rising up a planning hierarchy for the dimension location. Initially the conception hierarchy was "street < town < province < country". On rolling up, aggregation of data is done by ascending the hierarchy of location from the level of street to the level of the country. A roll-up involves summarizing the information on a dimension. The summarization rule may be Associate in Nursing mixture operate, like computing totals on a hierarchy or applying a collection of formulas like "profit = sales - expenses". General aggregation functions are also pricey to cipher once rolling up: if they can not be determined from the cells of the cube, they need to be computed from the bottom information, either computing them on-line (slow) or precomputing them for attainable rollouts (large space). Aggregation functions that will be determined from the cells square measure referred to as complex aggregation functions, and permit economical computation.
汇总是通过提升维度位置的计划层次结构来执行的。 最初,概念层次是“街道<城镇<省<国家”。 汇总时,数据的汇总是通过将位置层次结构从街道级别提升到国家/地区级别来完成的。 汇总涉及汇总有关维度的信息。 汇总规则可以是“护理中的助理人员”混合操作,例如在层次结构上计算总计或应用诸如“利润=销售-费用”之类的公式集合。 通用聚合函数一旦汇总就需要付出昂贵的代价:如果无法从多维数据集的单元中确定它们,则需要从底层信息中进行计算,要么在线(缓慢)计算它们,要么对其进行预先计算以实现可扩展性(大空间)。 由单元平方确定的聚合函数称为复杂聚合函数,可以经济地进行计算。
For example, it is easy to calculate COUNT, MAX, MIN, and SUM in OLAP, as this can be computed for each cell of the OLAP cube and then rolled up, since on overall sum (or count, etc.) is the sum of sub-sums, but it is difficult to support MEDIAN, as that must be computed for every view separately: the median of a collection isn't the median of medians of subsets.
例如,很容易在OLAP中计算COUNT,MAX,MIN和SUM,因为可以对OLAP多维数据集的每个单元格进行计算,然后汇总,因为总和(或计数等)是总和子和,但很难支持MEDIAN,因为必须分别针对每个视图进行计算:集合的中位数不是子集的中位数。
Let us understand it with a diagrammatic flow,
让我们以图解流程了解它,
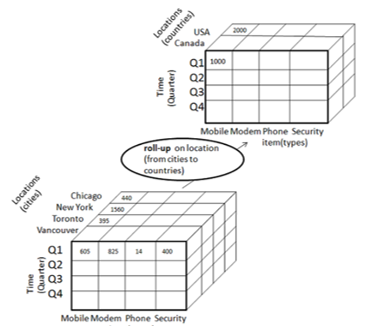
Fig 2.1 : Roll up Operation
图2.1:汇总操作
2.2。 向下钻取 (2.2. DRILL DOWN)
Drill-down is performed by stepping down the hierarchy for the dimension time. Initially, the conception hierarchy was "day < month < quarter < year." On drilling down, the dimension of time exists in descended from i.e. from the extent of the quarter to the extent of the month. When drill-down is performed, one or additional dimensions from the information cube are supplemental. It navigates knowledge from less elaborate information to extremely elaborate data.
通过在维度时间上降低层次结构来执行向下钻取。 最初,概念层次结构是“天<月<季度<年”。 在向下钻取时,时间的维数是从四分之一的范围降到一个月的范围。 执行向下钻取时,信息多维数据集中的一个或其他维度是补充。 它可以将知识从不太复杂的信息导航到极其复杂的数据。
Fig 2.2 : Drill Down Operation
图2.2:下钻操作
2.3。 OLAP切片 (2.3. OLAP SLICING)
The slice operation selects one specific dimension from a given cube and provides a replacement sub-cube.
切片操作从给定的多维数据集中选择一个特定的维度,并提供替换子多维数据集。
Slice is that the act of selecting an oblong set of a cube by selecting one worth for one in all its dimensions, making a replacement cube with one fewer dimension.
切片是指通过在其所有维度中为一个立方体选择一个值来选择一个长方形的立方体的动作,从而使替换的立方体的尺寸减少了一个。
The picture shows a slicing operation.
图片显示了切片操作。
Slicing is performed for the dimension "time" using the criteria time = "Q1".
使用标准时间=“ Q1”对维“时间”执行切片。
Subcube is formed by using or selecting one or two dimensions.
通过使用或选择一维或二维来形成子多维数据集。
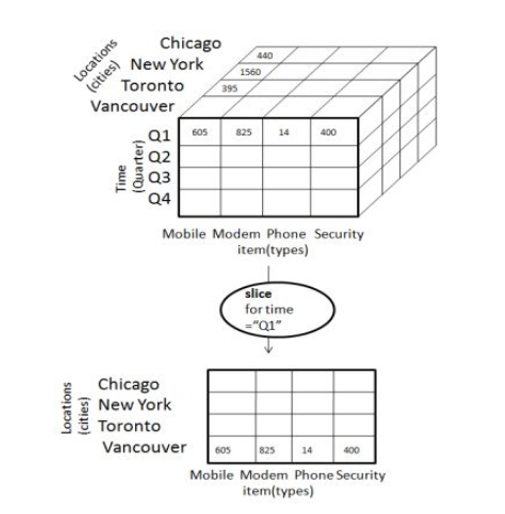
Fig 2.3 : OLAP Slicing
图2.3:OLAP切片
2.4。 OLAP骰子 (2.4. OLAP DICING)
Dice selects 2 or additional dimensions from a given cube and provides a brand new sub-cube. think about the subsequent diagram that shows the dice operation. The dice operation produces a subcube by permitting the analyst to choose specific values of multiple dimensions. the image shows a dicing operation. The dicing operation on the cube which involves three dimensions is based on the following selection criteria,
Dice从给定的多维数据集中选择2个或其他维度,并提供一个全新的子多维数据集。 考虑下面显示骰子操作的图。 骰子操作通过允许分析人员选择多维的特定值来生成子多维数据集。 该图显示了切块操作。 涉及三个维度的多维数据集上的切块操作基于以下选择标准,
(location = "Toronto" or "Vancouver")
(位置=“多伦多”或“温哥华”)
(time = "Q1" or "Q2")
(时间=“ Q1”或“ Q2”)
(item =" Mobile" or "Modem")
(项目=“移动”或“调制解调器”)

Fig 2.4 : Cube Dicing
图2.4:立方体切丁
2.5。 OLAP PIVOT (2.5. OLAP PIVOT)
The pivot operation is additionally referred to as rotation. It rotates the info axes seeable to produce an alternate presentation of knowledge. take into account the subsequent diagram that shows the pivot operation. Pivot permits AN analyst to rotate the cube in the area to check its varied faces. As an example, cities may well be organized vertically and product horizontally whereas viewing information for a selected quarter. Pivoting may replace the product with periods to check information across time for one product. The picture shows a pivoting operation: the full cube is turned, giving another perspective on the data.
枢转操作另外称为旋转。 它旋转可见的信息轴以产生替代的知识表示。 请考虑以下显示枢轴操作的图表。 Pivot允许分析人员旋转该区域中的多维数据集以检查其变化的面。 例如,在查看选定季度的信息时,很可能垂直组织城市,水平组织产品。 数据透视可能会用句点替换产品,以跨时间检查一种产品的信息。 该图显示了枢轴操作:旋转了整个立方体,从而为数据提供了另一个视角。
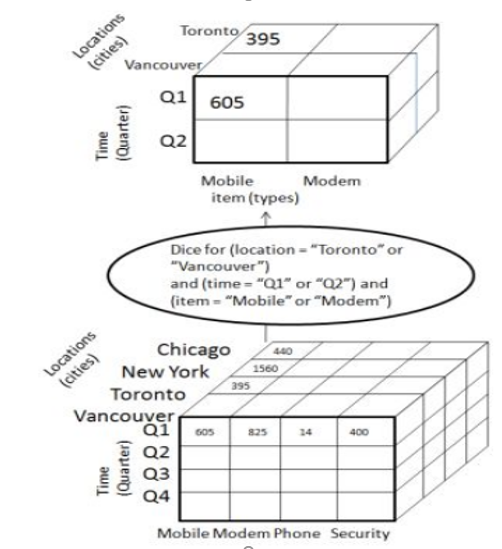
Fig 2.5 : Olap Pivot
图2.5:Olap枢轴
翻译自: https://www.includehelp.com/basics/olap-online-analytical-processing-olap-cube-and-operations.aspx
olap 多维分析








)

)


——栅格以及方程数值解估算)
算法)




