1. 串
1.1 串的定义
ADT String{
数据对象:D={ai|ai∈CharacterSet, i=1, 2, …, n, n≧0}
数据关系:R1={|ai-1, ai∈D, i=2, …, n}
基本操作:
生成一个值等于chars的串
复制一个串
判断串是否空串
比较串的大小
返回串元素的个数
将串清空
将串合并
返回串的指定下标的元素之后指定长度的字串
在某个串中查找规定子串,并返回指定下标的字符后第一次出现的位置
在某个串中用规定字串替代不重叠的另一规定字串
在串的指定下标的字符前插入一个指定子串
在串中删除一个规定下标开始指定长度的字串
销毁串
}1.2 串的存储结构
1.2.1 顺序存储
//----------串的定长顺序存储结构---------------
#define MAXLEN 255 //串的最大长度
typedef struct
{
char ch[MAXLEN+1]; //存储串的一维数组,从下标为1开始存储
int length; //串的当前长度
}SString;
//----------串的堆式顺序存储结构,按需分配长度----------------
typedef struct
{
char *ch; //如果是非空串,则按照串长分配存储区,否则ch为null
int length; //串的当前长度
}HString;1.2.2 链式存储
#define CHUNKSIZE 80
typedef struct Chunk
{
char ch[CHUNKSIZE]; //提高空间利用率(一个结点多个字符)
struct Chunk *next; //最后一个结点不满用非串字符填满
}Chunk;
typedef struct
{
Chunk *head, *tail; //尾指针便于操作
int length; //串的当前长度
}LString;1.3 模式匹配算法
1.3.1 BF算法
int Index_BF(SString S, SString T, int pos)
{//返回模式T在主串S中第pos个字符开始第一次出现的位置。若不存在,则返回值为0
//T非空,0int i=pos; int j=1; //初始化while (i<=S.length && j<=T.length) //如果两个串均没到串尾{if (S.ch[i]==T.ch[j]){++i; ++j;} //如果目前的字符匹配,则继续比较下一个字符else{i=i-j+2; j=1;} //如果失配,则将i退回到主串开始比较的下一个字符,j退回到字串的开头}if (j>T.length) return (i-T.length); //匹配成功else return 0; //匹配失败 }1.3.2 KMP算法
设计思想
失配时,主串指示器i不用回溯,利用已经得到的部分匹配,将模式串指示器j向右滑动尽可能远的距离后继续比较
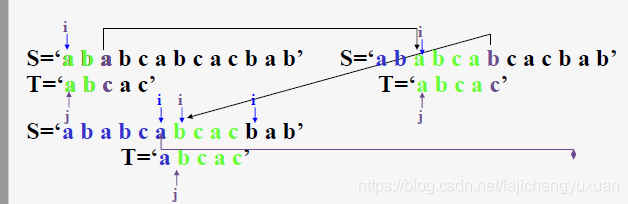


为此定义next函数,表示模式中第j个字符失配时,在模式串中需要重新与主串中该字符进行比较的字符的位置
故算法如下
int Index_KMP(SString S, SString T, int pos)
{ //利用模式串T的next函数求T在主串S中第pos个字符之后的位置
//其中T非空,1<=pos<=S.length
int i=pos; int j=1;
while (i<S.length && j<T.length) //两个串均未到达串尾
{
if(j==0 || S.ch[i]==T.ch[j]){++i; ++j;} //如果j为0或者目前的字符匹配,则继续比较下一个字符
else j=next[j]; //否则就将j置为next[j]
}
if (j>T.length) return (i-T.length); //匹配成功
else return 0; //匹配失败
}next函数求法
递推求值
由定义知,
next[1] = 0
设next[j]=k,表明有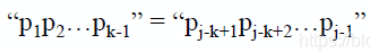
1k满足上式,此时next[j+1]的值有以下两种情况
(1)pk=pj,则有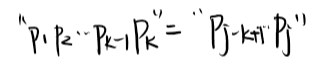
故
next[j+1]=k+1=next[j]+1
(2)pk≠pj
此时用把求next值的问题看成模式匹配的问题,模式串既是主串又是模式串
求next[j+1],第j+1个字符与主串失配,假设此时将k=next[j]及其前面的字符串滑过来与主串匹配,由于pk≠pj,此时第k个字母与主串失配,因此我们应当在它前面寻找k’=next[k]继续与主串匹配,以此类推,直到某个字符匹配成功或p[k+1]=1
故
next[j+1]=next[k]+1
算法如下:
void get_next(SString T, int next[])
{//求模式串T的next函数值并存入数组next
int i=1;next[1]=0;int j=0;
while (i<T.length)
{
if(j==0||T.ch[i]==T.ch[j]){++i; ++j; next[i]=j;} //如果j是0(开头)或者第i个字符等于第j个字符,则next[i+1]=j+1
else j=next[j]; //如果不等于,j回溯到next[j]
}
}但是,例如串"aaaab"与"aaabaaaab",第4个字母失配,但是还要将j=3,2,1依次与i=4比较,但由于j=1,2,3,4的字符都相等且i=4字符与j=4字符不等,因此可以直接比较i=5和j=1。
由此可见,当next[j]=k,而tj=tk时,不必比较,可以直接比较tj和tnext[k],以此类推
算法如下:
void get_nextval(SString T, int nextval[])
{//求模式串中next函数的修正值并存入数组nextval
int i=1;nextval[1]=0;int j=0;
while (i<T.length)
{
if(j==0||T.ch[i]==T.ch[j]){
++i;++j;
if(T.ch[i]!=T.ch[j]) nextval[i]=j;
else nextval[i]=nextval[j]; //如果第i个字符与第j个字符相等,j回溯到nextval[j]
}
else j=nextval[j];
}
}2. 数组
2.1 定义
ADT Array{
数据对象:ji = 0, …, bi-1, i=1,2,…,n
D = {aj₁j₂…jn | n>0 称为数组的维数,bi是第i维的长度}
ji是数组元素第i维下标,aj₁j₂…jn∈ElemSet}
数据关系:R = {R1, R2, …, Rn}
Ri = {}}
0<=jk<=bk-1, 1<=k<=n 且k≠i
0<=ji<=bi-2
aj₁…ji…jn, aj₁…ji+1…jn∈D, i = 2, …, n}
基本操作:
构造数组
销毁数组
赋值指定的元素
返回指定的元素值
}2.2 数组的顺序存储
位置下标:LOC(i,j)=LOC(0,0)+(n*i+j)L(可推广至n维)
2.3 特殊矩阵的压缩
对称矩阵(aij = aji)
以sa[a(a+1)/2]存储下三角,则对于下标k有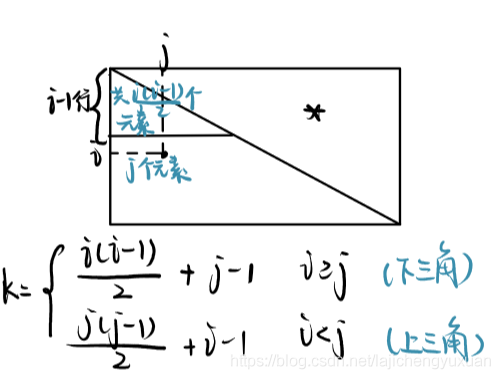
三角矩阵(只有半边有元素,剩下半边元素值相等)
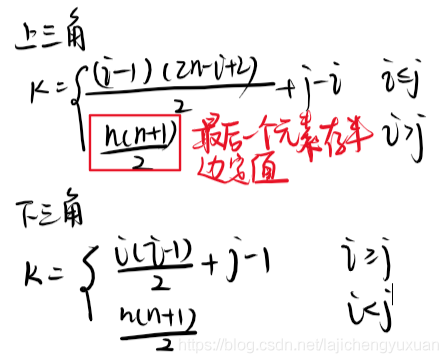
其它矩阵
(1)对角矩阵:找规律,压缩
(2)稀疏矩阵:三元组表(行下标,列下标,值)
3. 广义表
3.1 定义
一些结论
(1)元素可以是原子或者子表
(2)可以为其它广义表共享,可以共享其它广义表
(3)广义表是一个递归的表重要运算
(1)取表头:取出非空广义表的第一个元素,可以是单原子或者子表
(2)取表尾:取出除了第一个元素之外,其余元素构成的表
3.2 存储结构
表结点由标志域(1表示表结点,0表示原子结点),表头结点,表尾结点组成,原子由标志域和和值组成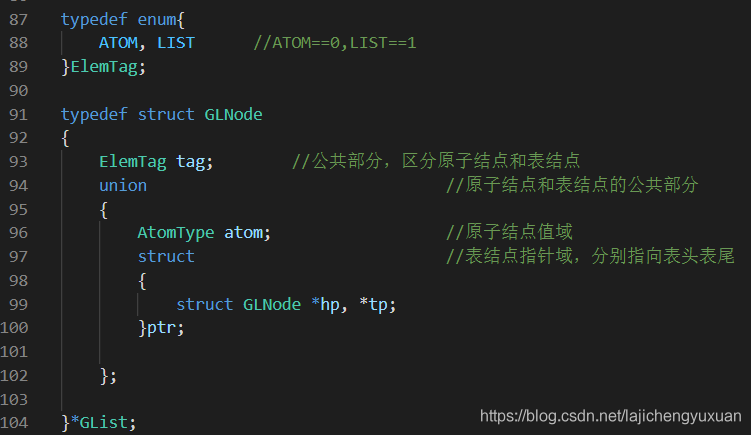
(a,(b,c,d))结构图示如下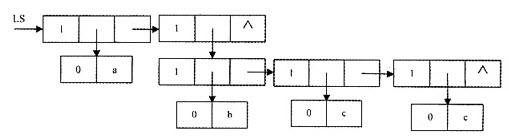

方法及示例)

方法与示例)
![[转载] 中国象棋软件-引擎实现(一)概述](http://pic.xiahunao.cn/[转载] 中国象棋软件-引擎实现(一)概述)
方法与示例)
)

方法与示例)


方法(带示例))

方法(带示例))

方法及示例)


方法及示例)
