最小硬币问题_进行更改的最小硬币数量

最小硬币问题

Description:

描述：

This is classic dynamic programming problem to find minimum number of coins to make a change. This problem has been featured in interview rounds of Amazon, Morgan Stanley, Paytm, Samsung etc.

这是经典的动态编程问题，用于寻找进行更改的最小硬币数量。亚马逊，摩根士丹利，Paytm，三星等公司的采访回合都突出了这个问题。

Problem statement:

问题陈述：

Given a value P, you have to make change for P cents, given that you have infinite supply of each of C { C₁, C₂, ... ,C_n} valued coins. Find the minimum number of coins to make the change. Return -1 if the change is not possible with the coins provided.

给定一个值P ，由于您拥有C {C ₁ ，C ₂ ，...，C _n }个有价硬币的无限供应，因此您必须为P美分进行更改。 找到进行更改的最小硬币数量 。如果提供的硬币无法找零，请返回-1 。

    Input:
Amount P=13
Coin values are:
1, 4, 5 
Output:
3

Explanation with example

举例说明

Let's solve the above example. Total amount is 13 and we have coins with values 1, 4 and 5.

让我们解决以上示例。总金额为13，我们有价值分别为1、4和5的硬币。

Since, we are to find minimum number of coins and we have infinite number of coin for any denomination, it's apparent that we would go for greedy. We should pick the coin with maximum denomination and keep trying with that until the remaining amount of the change is less the denomination of the coin. Then on course we keep choosing the next best one. So, the algorithm would be like.

因为，我们要找到最小数量的硬币，而对于任何面额我们都拥有无限数量的硬币，所以显然我们会贪婪。我们应该选择面额最大的硬币，并继续尝试直到零钱的剩余金额少于硬币面额为止。然后，当然我们会继续选择次佳的。因此，该算法将是这样。

    1) Let, count=0 to count minimum number of coin used
2) Pick up coin with maximum denomination say, value x
3) while amount≥x
amount=amount-x
count=count+1 
4) if amount=0
Go to Step 7
5) Pick up the next best denomination of coin and assign it to x
6) Go to Step 2
7) End. count is the minimum number of coin used.

Let's see whether the above greedy algorithm leads to the desired result or not.

让我们看看上面的贪婪算法是否导致了期望的结果。

    So, we would pick up 5 first from {1, 4, 5}
We would pick 5 two times
Now amount=3, count=2
Next best coin is 4 but 4 > amount
Next best coin is 1
We would pick 1 three times
Amount=0 and count=5
So, minimum number of coins needed for the change is 5.
But is it really minimum?
If we choose one coin with denomination 5 and two coins with denomination 4, 
it would make the change and coins needed here is (2+1) = 3 
So, greedy does not work as the local optimum choices doesn't make 
global optimum choice. Hence, we need dynamic programming.

Problem Solution Approach

问题解决方法

We have amount M and n number of coins, {C₁, C₂, ..., C_n}

我们有M个和n个硬币， {C ₁ ，C ₂ ，...，C _n }

Now,

现在，

We have two choice for any C_j,

对于任何C _j ，我们都有两种选择。

Use C_j and recur for amount M-C_j
使用C _j并递归MC _j
Don't use C_j and recur for amount M with other coins
不要使用C _j并与其他硬币重现金额M

(m)= minimum number of coins needed to change amount m

(m)=找零数量m所需的最小硬币数量

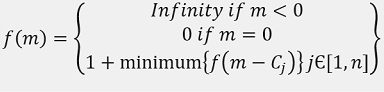
We can formulate the above recursion using DP.

我们可以使用DP来制定上述递归。

    // (for any amount 0 to M, minimum number of coins needed is initially infinity) 
1) Initialize DP[M+1] with INT_MAX. 
2) DP[0]=0 //base case of above recursion
3)  for  i=1 to M //iterate amounts
for any coin C_j
If i>=C_j  && DP[i-C_j]≠INT_MAX && DP[i-C_j]+1<DP[i])
DP[i]=DP[i-C_j]+1; //update value
End for
End for   
The result is DP[M]

C++ implementation:

C ++实现：

#include <bits/stdc++.h>
using namespace std;
int coin_change(vector<int> a, int m, int n)
{
//recursive implementation//
// if(m<0)
// return;
// if(m==0){
//     if(count<min_count)
//     min_count=count;
//     return;
// }
// for(int i=0;i<n;i++){
//     coin_change(a,i,m-a[i],n,count+1);
//     coin_change(a,i+1,m-a[i],n,count+1);
// }
///DP implementation///
//base value
int DP[m + 1];
//initialize
for (int i = 1; i <= m; i++)
DP[i] = INT_MAX;
DP[0] = 0;
for (int i = 1; i <= m; i++) {
for (int j = 0; j < n; j++) {
// if amount > coin value
if (i >= a[j] && DP[i - a[j]] != INT_MAX && DP[i - a[j]] + 1 < DP[i])
// if updation possible update for minimum value
DP[i] = DP[i - a[j]] + 1;
}
}
return DP[m];
}
int main()
{
int n, item, m;
cout << "Enter amount to be changes:\n";
cin >> m;
cout << "Enter number of coins:\n";
cin >> n;
cout << "Enter coin values\n";
vector<int> a;
for (int j = 0; j < n; j++) {
scanf("%d", &item);
a.push_back(item);
}
int ans = coin_change(a, m, n);
if (ans == INT_MAX)
cout << "Coin change not possible" << endl;
else
cout << "Minimum number of coins needed: " << ans << endl;
return 0;
}

Output

输出量

RUN 1:
Enter amount to be changes:
13
Enter number of coins:
3
Enter coin values
1 4 5
Minimum number of coins needed: 3
RUN 2:
Enter amount to be changes:
11
Enter number of coins:
2
Enter coin values
4 5
Coin change not possible