Lasso与岭回归的同和异

1. Lasso、岭回归都可以预防模型过拟合

2. Lasso回归惩罚项为L1正则，岭回归为L2正则

3. Lasso回归可用来特征选择，岭回归则不能

4. Lasso回归用坐标下降法求解，岭回归用梯度下降法求解。

为什么Lasso可用于特征选择，而岭回归不能

我们首先来看一下Lasso、岭回归的目标函数。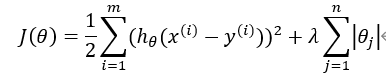

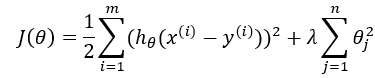
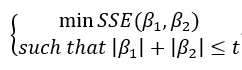
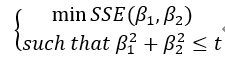
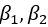假设在二维特征上，并转化为约束问题为：

其中SSE表示残差平方和，也就是目标函数的前半部分，代表特征权重，反应在二维图像上如下所示，其中红色圈代表SSE等高线，越往外SSE值越小，并且满足约束条件，在Lasso回归上既可以满足最优解，又能使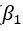为0，多边形更容易和等高线碰撞出稀疏解。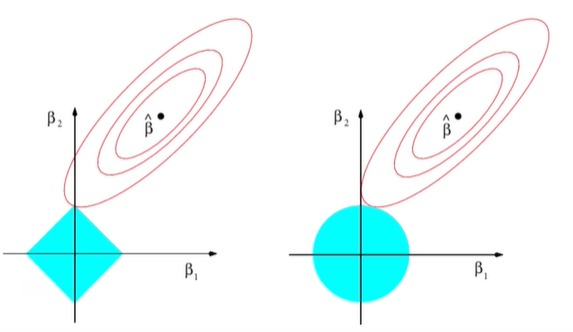

梯度下降法求解目标函数

目标函数：

                                     

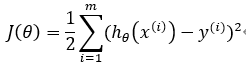
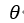首先目标函数是个凸函数，沿着负梯度方向迭代 总能找到最小值，具体步骤如下：

1. 初始化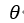(随机初始化)

2. 沿着负梯度方向迭代，更新后的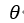使得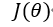更小，如下公式所示，其中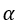为学习率、步长。

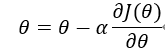
其中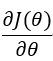求解如下所示：

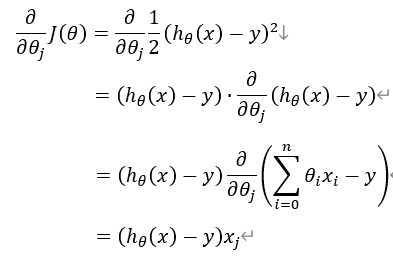
怎么解决欠拟合和过拟合问题？

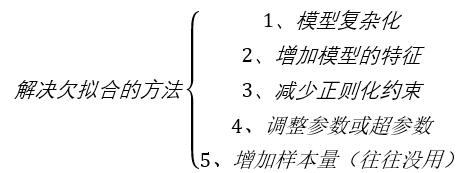
使用线性回归的必要条件

线性、独立、正态、齐性。(1)自变量与因变量之间存在线性关系        可以通过绘制散点图矩阵进行考察因变量随各自变量值的变化情况。如果因变量与某个自变量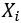之间呈现出曲线趋势，可尝试通过变量变换予以修正，常用的变量变换方法有对数变换、倒数变换、平方根变换、平方根反正弦变换等。(2)各观测间相互独立       任意两个观测残差的协方差为0 ，也就是要求自变量间不存在多重共线性问题。对于如何处理多重共线性问题，我们之后会讨论。(3)残差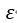服从正态分布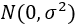。(4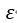的大小不随所有变量取值水平的改变而改变，即方差齐性。