事先说明:笔者初三,如在叙述中有不严谨的地方,还请诸位指出,自当感激不尽。
一.什么是斜坐标系
众所周知,我们目前平面中使用相当广的坐标系是笛卡尔发明的平面直角坐标系。然而,笛卡尔真的只使用了这一种坐标系吗?显然不是的。事实上,笛卡尔最先使用的是一种斜坐标系,即x轴与y轴夹角不为π/2的坐标系,这种坐标系更为一般化,也更自然。
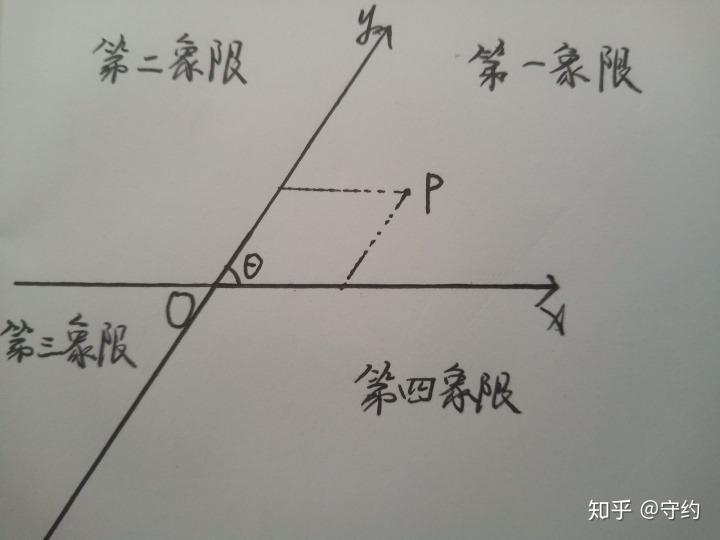
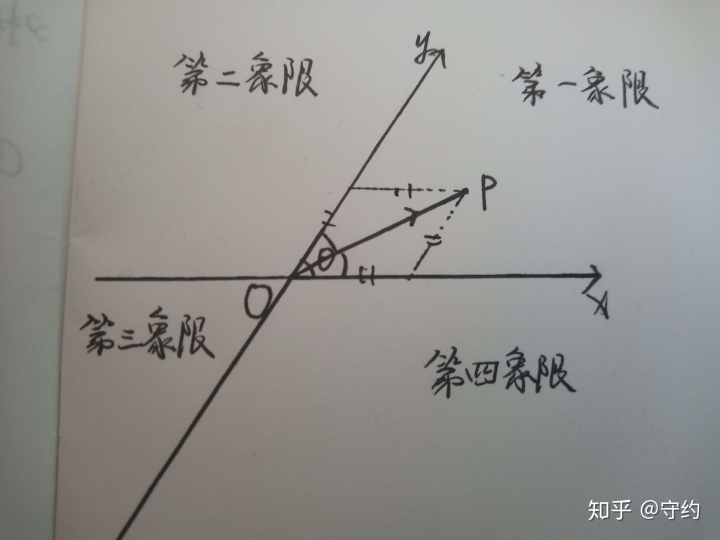
由此,对于一类题目如下:
△ABC平面内一动点p满足向量Ap=λ(向量AB/|向量AB|+向量AC/|向量AC),我们根据斜坐标系可以直接看出它在∠BAC的角平分线上运动。
另附一些斜坐标系的小内容,感兴趣的不妨自己推理一下:
1.与x轴垂直的直线,k=-1/cosθ 2.与y轴垂直的直线,k=-cosθ
3.若以三角形abc的a为原点,以两边方向为坐标轴方向建立平面斜角坐标系,(ab对应x轴,ac对应y轴)设Xb=A,Yc=B,则有:三角形垂心H(cosθ(B-Acosθ)/sin²θ,cosθ(A-Bcosθ)/sin²θ)外心Q(A-Bcosθ/2sin²θ,B-Acosθ/2sin²θ)于是有向量QH=向量Qa+向量Qb+向量Qc(我才不会告诉你这是我证这个结论时作死不用垂心伴随外接圆模型得到的)
4.规定同3,重心G(⅓a,⅓b)
5.设直线的倾斜角为α,则k=sinα/sin(θ-α)
6.在斜坐标系内,若两直线垂直且斜率存在,则满足k1k2+cosθ(k1+k2)=-1
二.斜坐标系内一些运算公式
1.两点之间距离公式
首先,设向量AB=(a,b)将向量AB坐标转化为直角坐标系中坐标,则变成(a+bcosθ,bsinθ)对此应用直角坐标系中向量模长公式,则有|AB|=√a²+2abcosθ+b²(sin²θ+cos²θ)=√a²+b²+2abcosθ,这就是最终得到的距离公式了。
2.向量内积公式
同样的套路,只要将向量AB变换成(a+bcosθ,bsinθ),向量CD变换成(c+dcosθ,dsinθ)那么向量AB·向量CD=ac+bdcos²θ+ad cosθ+bc cosθ+bdsin²θ=(ac+bd)+cosθ(ad+bc),即为所求
3.点到直线距离公式
这个我不能无脑搞了,那样要算死人QAQ,请看图:
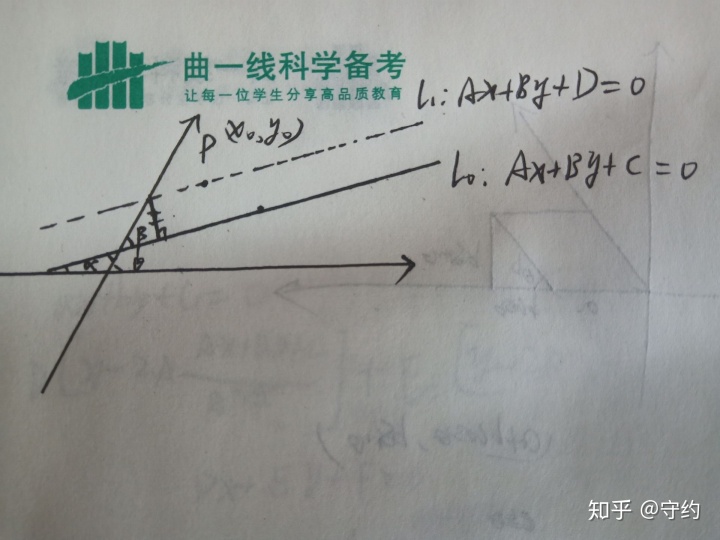
我们设点P(Xo,Yo),直线lo:Ax+By+C=0,过p做lo的平行线l1,那么点p到lo的距离转化为l1与lo的距离。在l1与y轴交点处做lo的垂线。设角α,β,θ如图。
先求l1,lo与y轴交点间长度:将x=0代入,则有:
By1+C=0 ,y1=-C/B
By2+D=0 ,y2=-D/B
考虑到未知p的方位(可能在lo上方或下方),故线段l长度表示为|(C-D)/-B|,又因为有
AXo+BYo+D=0,则D=-AXo-BYo,所以l长度为|(Ax0+By0+C)/-B|
观察到我们所求的h=|l|·sinβ=|l|·sin(θ-α)=|l|·(sinθcosα-sinαcosθ)
我们单独研究α如图:
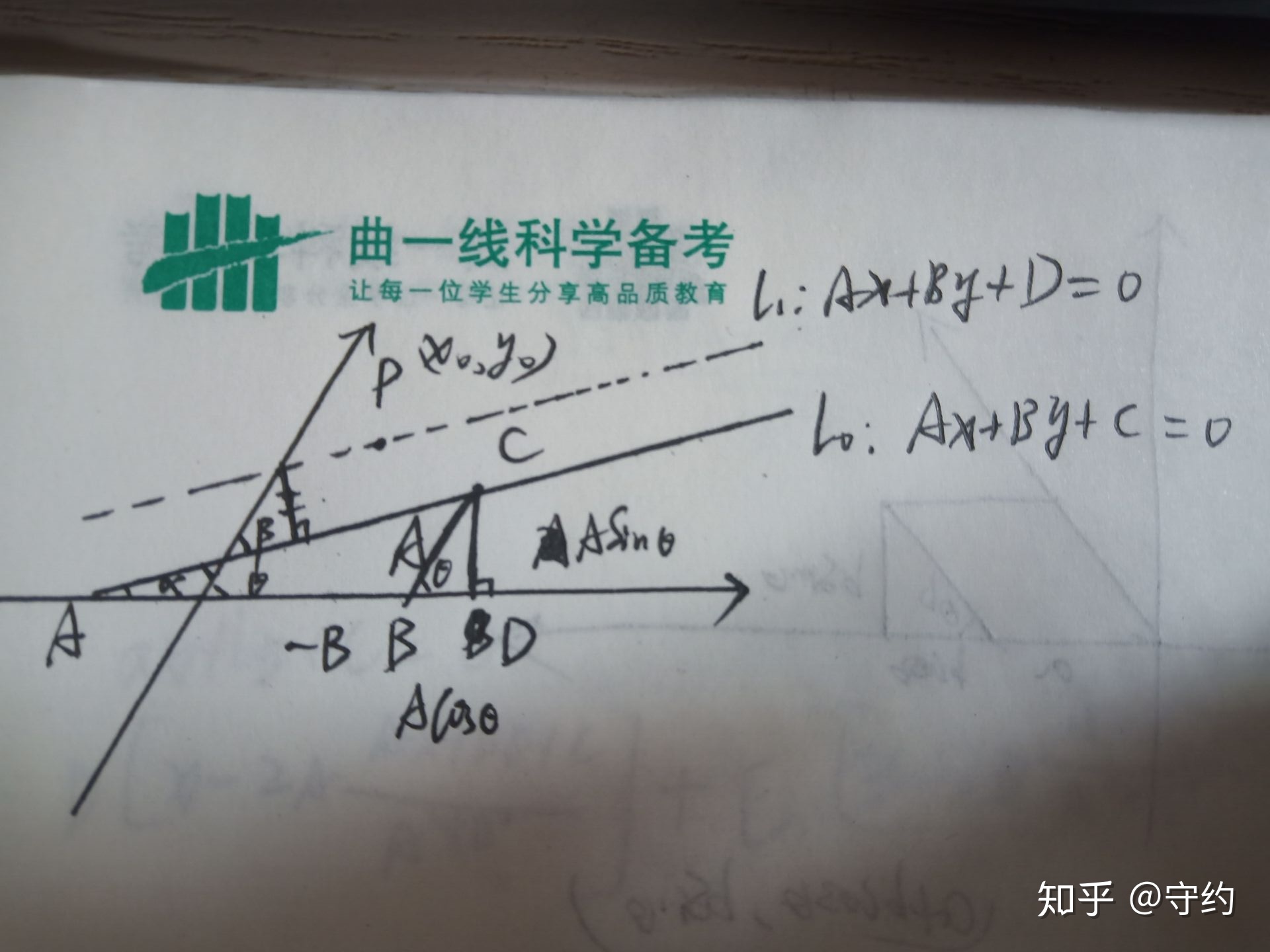
取lo上一点c,设它与x轴交点为a,并作cd⊥x轴,cb∥y轴,并且令向量ab=(-B,0),向量bc=(0,A),于是向量bd=(cosθ·A,0)向量dc=(0,sinθ·A)那么在三角形acd中,可以解得ac=√(cos²θ+sin²θ)A²+B²-2ABcosθ=√A²+B²-2ABcosθ,
故:sinα=Asinθ/√A²+B²-2ABcosθ
cosα=Acosθ-B/√A²+B²-2ABcosθ
(正负性问题在此不做赘述了)
将得到的结果代入上式:
h=|(Ax0+By0+C)/-B|·[(Acosθ-B)sinθ-Asinθcosθ]/√A²+B²-2ABcosθ
=|(Ax0+By0+C)/-B|·(-Bsinθ)/√A²+B²-2ABcosθ,我们大胆地化简,消去-B
得到h=|(Ax0+By0+C)|·sinθ/√A²+B²-2ABcosθ,此时发现:
1.sinθ∈(0,1),即分式上方部分>0
2.A²+B²-2ABcosθ>0,即分式下方部分>0
这证明化简正确。
综上可得点到直线距离公式为:h=|(Ax0+By0+C)|·sinθ/√A²+B²-2ABcosθ
4.等和线
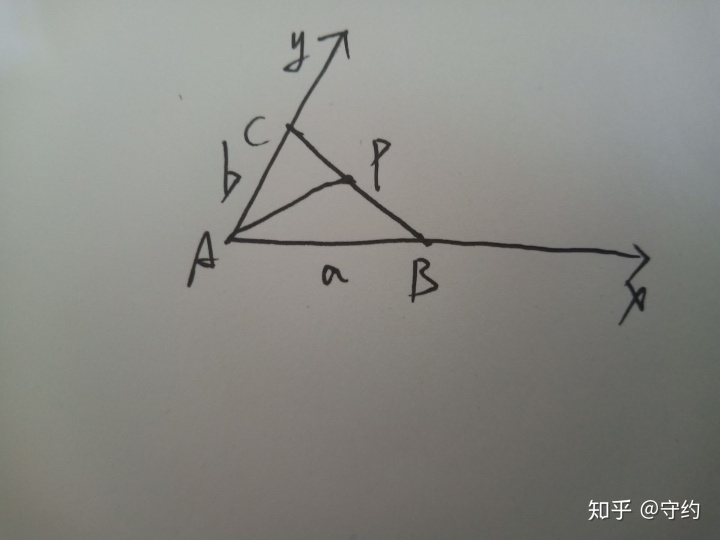
设|AB|=a,|AC|=b,P(ma,nb)
可解得lBC:y=-b/a·x+b,变形为x/a+y/b=1
∴ma/a+nb/b=1,即m+n=1,得证。同样易构“等差线”。
5.奔驰定理
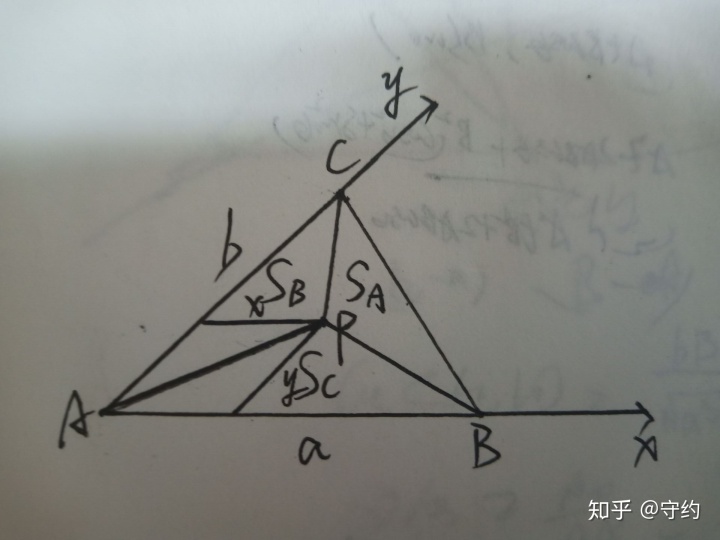
设B(a,0)C(0,b)P(x,y)S△ABC=S,则:
SB=x/a ·S,向量BP=(x-a,y)
Sc=y/b ·S,向量CP=(x,y-b)
SA=(1-x/a-y/b)S,向量AP=(x,y)
∴向量AP·SA+向量BP·SB+向量CP·SC=((x-x²/a-xy/b+x²/a-x+xy/b)·S,(y-xy/a-y²/b+xy/a+y²/b-y)·S)=0向量,得证。
利用斜坐标系,我们也可以得到p在△ABC外的情况,过程类似不再赘述,结论是:在△ABP、△ACP、△BCP中,图形除了与AB边(或BC边、AC边)有交点外与三角形ABC再无交集的,在前面加上负号,则等式依然成立。
下面附一道例题:
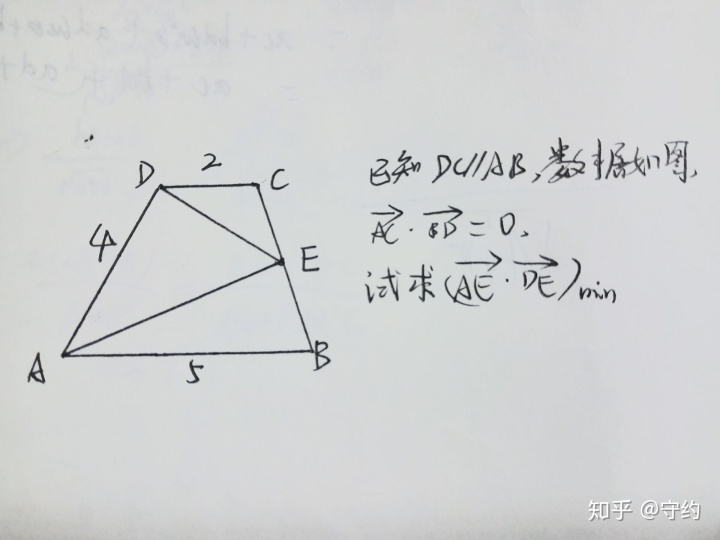
解:以AB为x轴,AD为y轴建立斜坐标系
则有C(2,4)B(5,0)D(0,4)lCB:y=-4/3x+20/3,即4x+3y-20=0
∴(2,4)·(-5,4)=0
∴-10+16-12cosθ=0,得θ=π/3
由极化恒等式,取AD中点F,则向量AE·向量DE=EF²-AF²
由点到直线距离公式得:EF²min=(7·根号3)²/(16+9-12)=147/13
∴(向量AE·向量DE)min=147/13 -4=95/13















![mysql_ping()函数的作用以及返回值的类型正确的是,[单选] mysql_ping()函数的作用以及返回值的类型正确的是:()...](http://pic.xiahunao.cn/mysql_ping()函数的作用以及返回值的类型正确的是,[单选] mysql_ping()函数的作用以及返回值的类型正确的是:()...)
送给大家...)


