
导读
1. 什么是图?图的存储方式?
2. 图的遍历(深度优先搜索,广度优先搜索)
3. 最短路径
1. 什么是图?图的存储方式?
前面总结了“树”这种数据结构,而这篇博客总结的是更为复杂的一种数据结构:图(graph),它表明了物件与物件之间的“多对多”的一种复杂关系。图包含了两个基本元素:顶点(vertex, 简称V)和边(edge,简称E)。
有向图与无向图
如果给图的每条边规定一个方向,那么得到的图称为有向图。在有向图中,从一个顶点出发的边数称为该点的出度,而指向一个顶点的边数称为该点的入度。相反,边没有方向的图称为无向图。
有权图与无权图
如果图中的边有各自的权重,得到的图是有权图。比如地铁路线图,连接两站的边的权重可以是距离,也可以是价格,或者其他。反之,如果图的边没有权重,或者权重都一样(即没有区分),称为无权图。
连通图
如果图中任意两点都是连通的,那么图被称作连通图。图的连通性是图的基本性质。无向图中的一个极大连通子图称为其的一个连通分量。有向图中,如果对任意两个顶点
图的存储
常用的存储方式有两种:邻接矩阵和邻接表。
邻接矩阵
采用一个大小为
一般情况下我用的邻接矩阵的结构和初始化代码如下,具体会根据使用需求有所改动。
struct GNode{int Nv; // number of verticesint Ne; // number of edgesint G[MaxVNum][MaxVNum];
};
typedef struct GNode *MGraph;
MGraph Graph = new GNode[MaxVNum];// 初始化图
void InitGraph(int N,int E){Graph->Nv = N;Graph->Ne = E;for (int u=0;u<=N;u++)for (int v=0;v<=N;v++)Graph->G[u][v]=INF;
}
//插入边(这里是有权重的无向边)
void InsertEdge(int u,int v,int weight){Graph->G[u][v]= weight;Graph->G[v][u]=weight;
}邻接表

另外,之前做习题的时候也会习惯用个二维数组来存储邻接表,比如上面的
一般情况下我用的代码如下,会根据具体需求有大改动。
typedef struct VNode *AdjNode;
struct VNode{int node;AdjNode next;
};
AdjNode Graph = new VNode[MaxV];void InitGraph(int N,int E){Graph->Nv = N;Graph->Ne = E;for (int i=1;i<=N;i++){(Graph+i)->node=i;(Graph+i)->next=NULL;}
}
// 插入有向边
void InsertEdge(int u,int v){AdjNode tmp1=new VNode;AdjNode tmp2 = new VNode;tmp1->node = v;tmp1->next = (Graph+u)->next;(Graph+u)->next=tmp1;tmp2->node = u;tmp2->next = (Graph+v)->next;(Graph+v)->next=tmp2;
}2. 图的遍历
图的遍历最常用的有两种:深度优先搜索(Depth-first Search, DFS)和广度优先搜索(Breadth-First Search, BFS)。
深度优先搜索
有点类似于树的前序遍历,即从一个选定的点出发,选定与其直接相连且未被访问过的点走过去,然后再从这个当前点,找与其直接相连且未被访问过的点访问,每次访问的点都标记为“已访问”,就这么一条道走到黑,直到没法再走为止。没法再走怎么办呢?从当前点退回其“来处”的点,看是否存在与这个点直接相连且未被访问的点。重复上述步骤,直到没有未被访问的点为止。
从上述文字表述可以看出,DFS很适合使用递归,其代码如下:
int visited[MaxN]={0}; //记录顶点的访问状态
int result[MaxN]; //result数组记录DFS遍历结果
int N,E,k;// N为顶点数,E为边数,k记录遍历结果下标void DFS(int v){visited[v]=1;result[k++]=v;for (int i=0;i<N;i++){if (G[v][i]==1 && visited[i]==0)DFS(i);}
}int main(){for (int i=0;i<N;i++){k = 0;if (visited[i]==0){DFS(i);//用{}打印出一个连通分量cout<<"{ ";for (int j=0;j<k;j++)cout<<result[j]<<' ';cout<<"}"<<endl;}}
return 0;
}广度优先搜索
有点类似于树的层序遍历,也就是像剥洋葱一样,“一层一层地剥开♩♩♩”。即从一个选定的点出发,将与其直接相连的点都收入囊中,然后依次对这些点去收与其直接相连的点。重复到所有点都被访问然后结束。
类似树的层序遍历,BFS同样可以通过一个队列来实现,代码如下:
int visited[MaxN]={0}; //记录顶点的访问状态
int result[MaxN]; //result数组记录BFS遍历结果
int N,E,k;// N为顶点数,E为边数,k记录遍历结果下标void BFS(int v){queue<int> q;q.push(v);visited[v]=1;result[k++]=v;while(!q.empty()){int u = q.front();q.pop();for(int i=0;i<N;i++){if (G[u][i]!=0 && visited[i]!=1){visited[i]=1;q.push(i);result[k++]=i;}}}
}int main(){for (int i=0;i<N;i++){k = 0;if (visited2[i]==0){BFS(i);//用{}打印出一个连通分量cout<<"{ ";for (int j=0;j<k;j++)cout<<result[j]<<' ';cout<<"}"<<endl;}}
return 0;
}上述BFS和DFS的时间复杂度均为。
3. 最短路径
简而言之,最短路径就是找图中连接两个顶点所有边权重和最小的路径。
- 对无权图而言,即是找边最小的路径;
- 如果给定起点,则是单源最短路径,即从一固定起点到任意终点的最短路径;
- 如果起点不确定,则是多源最短路径,即求任意两个顶点的最短路径。
单源最短路径
对于无向图而言,可以借助BFS的“剥洋葱”特性,看从起点到终点需要剥几个洋葱圈,剥的层数即是最短路径长度。
对于有向图而言,就不得不提到一个煊赫的名字:Dijkstra算法。陆续泛听了几个版本的数据结构,这个名字简直太深入人心。
- Dijkstra算法
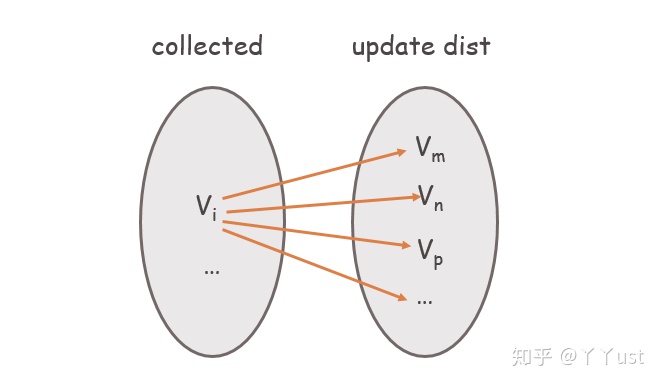
具体来说,Dijkstra算法的核心在于:从起点(或者说源点)开始,将其装进一个“袋子”里,然后不断往这个袋子里搜罗顶点,当顶点收进去后,能保证从源点到该顶点的当前最短路径是确定的。每次收录的顶点是在未收录的集合里寻找最短路径最小的点(即离源点最近的点),然后将与收进去的顶点直接相连的点的最短路径进行更新。
如下图所示,
值得注意的是:Dijkstra算法不适用于存在负权重边的图。
给出Dijkstra代码前先对保存最短路径的数组dist[]和收录状态的数组collected[]进行初始化:和源点直接相连的点的最短路径即为该边的权重,其余均初始化为一个很大的(一看就不可能的数)INF;collected中所有值初始化为false。
int dist[MaxN];
bool collected[MaxN];void InitDist(int start){for (int i=0;i<Graph->Nv;i++){dist[i]=Graph->G[start][i];collected[i]=false;}
}然后,我们需要寻找下一步被收录的点:即在所有未被收录的点中寻找dist最小的点。如果不存在(最小值为无穷大INF),则返回错误标识-1。这一步找最小值,我们可以每次都将所有顶点扫描一遍获得,也可以很自然地想到将dist存在一个最小堆(优先队列)里。对于前者,因为每次收录都要扫描一次所有顶点,有
int findMinDist(int start){int MinD = INF;int MinV;for (int end =0;end<Graph->Nv;end++){if (collected[end]==false && dist[end]<MinD){MinD=dist[end];MinV=end;}}if (MinD<INF)return MinV;elsereturn -1;
}然后是Dijkstra算法主程序:在初始化后,先将源点收录进袋,并且源点的最短路径设为0, 然后开始循环寻找能被收录的点:如果接受到的是错误标识-1,说明找不到符合要求的点了,程序结束。如果找到了,则先将这个点收录进去,记录为s; 然后遍历从s出发的所有边,对没有收录的点,更新他们的最小路径值。更新的依据是:如果这个点t的当前的最小路径值,大于s点的最小路径值与s到t边的权重值之和,则更新为
bool dijkstra(int start){InitDist(start);dist[start]=0;collected[start]=true;int s;while (1){s = findMinDist(start);if (s==-1)break;collected[s]=true;for (int t=0;t<Graph->Nv;t++){// if W is not collected and s->t existsif (collected[t]==false && Graph->G[s][t]<INF){// check if it is a negative-weighted edgeif (Graph->G[s][t]<0) return false;// check if dist[t] needs updateif (dist[t]>dist[s]+Graph->G[s][t])dist[t]=dist[s]+Graph->G[s][t];}}}return true;
}多源最短路径
按照上面已有的Djikstra算法,可以直接将Djikstra算法在每个顶点调用一遍,然后找最小值。时间复杂度为:
直接找dist最小:。
最小堆维护dist:。
另外还有一种更为直接的算法是Floyd算法,且代码看着简洁直观优美。。。
bool Floyd(){int i, j, k;for (k=0;k<Graph->Nv;k++)for (i=0;i<Graph->Nv;i++)for (j=0;j<Graph->Nv;j++)if (dist[i][k]+dist[k][j]<dist[i][j]){dist[i][j]=dist[i][k]+dist[k][j];if (i==j && dist[i][j]<0) //发现负值回路return false;}return true;
}三重循环嵌套,可以直观看出时间复杂度为
参考资料:
- coursera的《算法分析与设计》(以前的课程)
- MOOC网的《数据结构与算法》
小结
距离上次更新已经有很长的时间,一方面是因为没整理好,包括现在记录的也觉得很混乱,就这么先把笔记记下来吧,不然时间久了更迷糊。另一方面是身体原因,年纪轻轻竟然椎间盘膨出了,不知道知乎上有没有啥治疗良方,反正去了好几次医院都说没事,直到痛得不行让拍CT了才知道是腰椎间盘膨出☹☹☹
扯远了❦❦❦,剩下还有一些最小生成树,和拓扑排序啥的等我更明白点再写吧~~~









 for 'xxx' is missing)



案例...)

)



