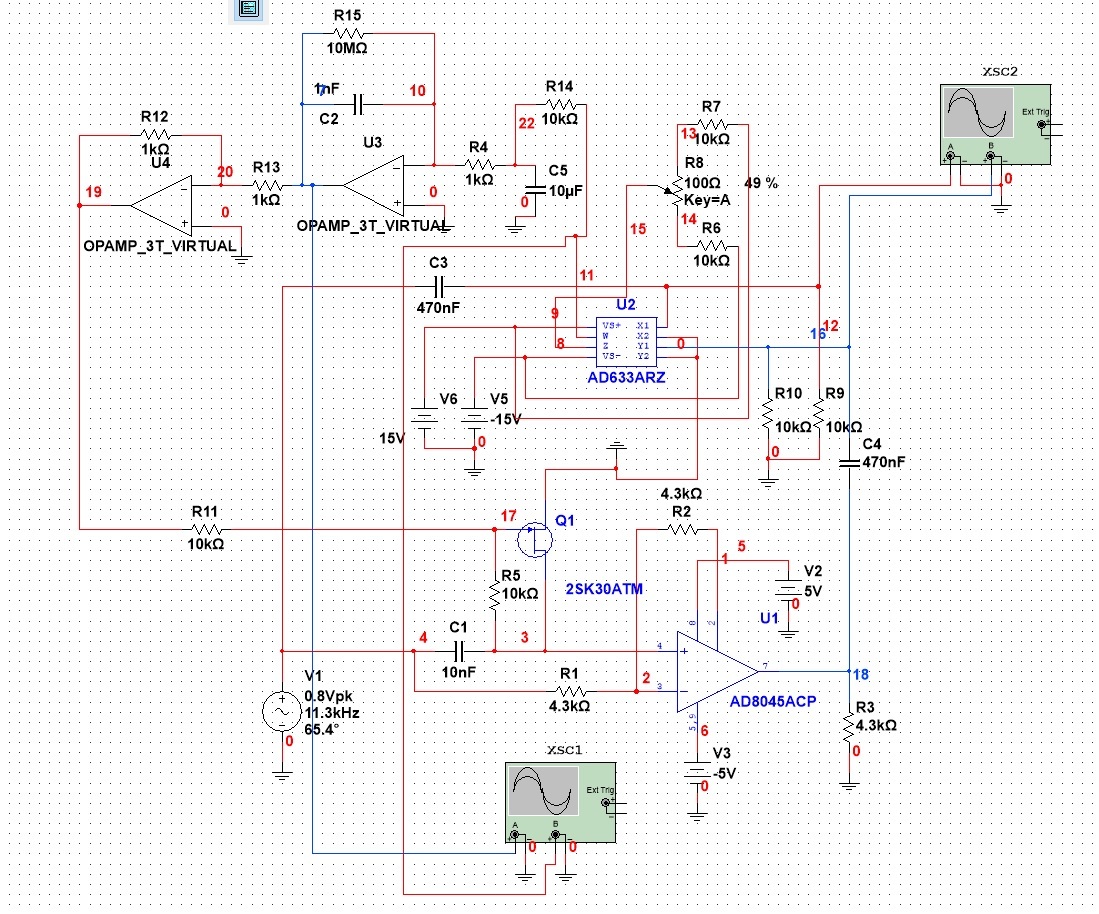
移相电路就是对输入信号(一般是正弦波)进行相位控制,而不改变其幅度,本推文以移相电路为例,展示模拟电路的反馈设计技巧与方法:
一、全通滤波器实现移相


以上是两种移相电路 的原理,其输出幅度保持不变,移动的相位随R3和C而改变,在C和R3确定时其移相是arctan函数,非线性的,当WR3C较小时,近似线性arctan(x)=x,|x|<=0.5,仿真伯德特的相位如下:
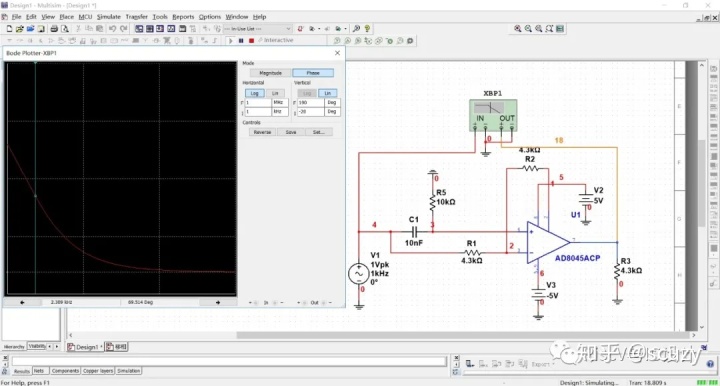
上图可见,在WR3C较小时,是线性相移,即确定最最高频率Wmax后可以反向计算R3C<=0.5/Wmax,确定线性相移应用的时间常数R3C。
二、反馈控制设计举例
现在需要设计一个电路,实现输入频率在一定范围内变化、输入信号的初始相位变化时,输出信号始终超前输入信号90°,而输出信号幅度保持与输入信号幅度相同。这该如何实现?
应用前述的全通滤波器,好像有希望实现,关键是要能调整C与R3,而且要刚好调整到对输入信号移相90°,这是问题的关键。我们把问题细分一下:
1)如何改变C或R3?
2) 如何检测相位差?这其实就是要根据相位差来反馈控制C或R3的变化,可以采用模拟控制也可用数字控制方式。
先说1),改变C当然不能人去手动调节,要用电信号自动调节,首先想到的就是反向偏置的变容二极管,本推文我们不选择改变C,如果是改变R3那么如何做?当然不能用普通电位器了
,我们还是需要能电控改变阻值的东东:
a)不少人可能首先想到的是数字电位器,这个有些问题:首先太复杂,意味着你要使用单片机,而且数字电位器都是离散电阻值,假设一步对应100欧姆,1.5khz时需要900欧姆,刚好合适,而1.525khz输入频率,如果需要923.56欧,就完了,因为一步对应100欧姆的数字电位器只有900欧姆、1000欧姆,没有923.56欧姆,会影响控制精度,所以数字电位器不是最佳方案。那么你非要使用数字电位器又该怎么办?那也不是没有办法,只是精度差一些:比如,你可以参考PWM控制的思路,在20次控制中,1000*(20-x)/20+900*x/20=923.56,计算出x次选择900欧,剩下(20-x)选择1000欧。
b)还有就是选择JFET管,工作在可变电阻区,这是非常好的方案,只是要控制JFET的工作电压和扩展JFET的线性,下面详述
再说2),这里关键是需要一个鉴相器,来检测相位差,二极管鉴相器、二极管平衡环状鉴相器、乘法器....都可以做鉴相器,这里为了简单选择乘法器做鉴相器
先给出整体仿真电路和仿真实验结果:
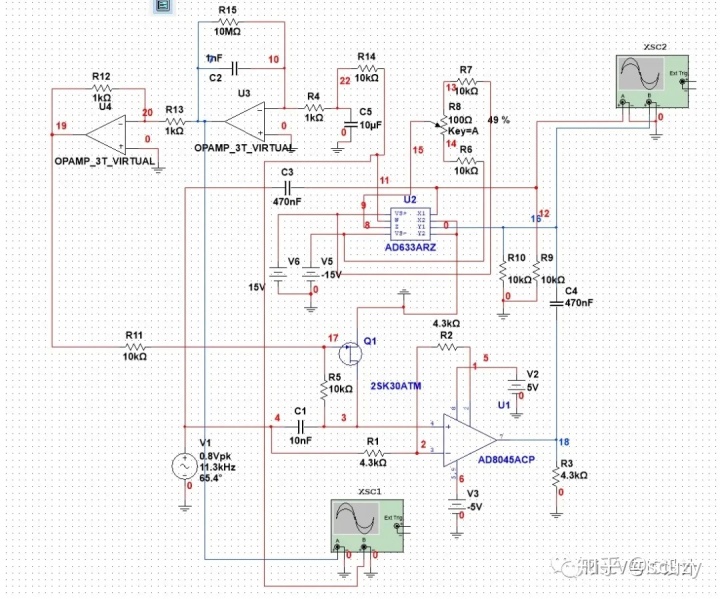
下面看看反馈跟踪控制电路,其由鉴相器和JFET可变电阻构成:
1)鉴相器这里采用的是乘法器,把输出信号Asin(wt+Po)与输入信号Asin(wt+P1)相乘,sina*sinb=-0.5[cos(a+b)-cos(a-b)],当两者差90°时结果只有cos2wt 二倍频分量,无直流分量,而非90°相位差时,会有一个直流分量0.5*cos(Po-P1), 推文中使用一个一阶RC取出直流分量,然后对直流分量进行积分,这个积分器是必须的,其作用就是如果误差没有消除就不断增强调节作用,此处如果换成放大器就没有持续调节作用了,其实这就是PID控制中的积分环节,目的就是消除最终的稳态误差!此电路只是临时起意设计的,参数还没有优化计算。
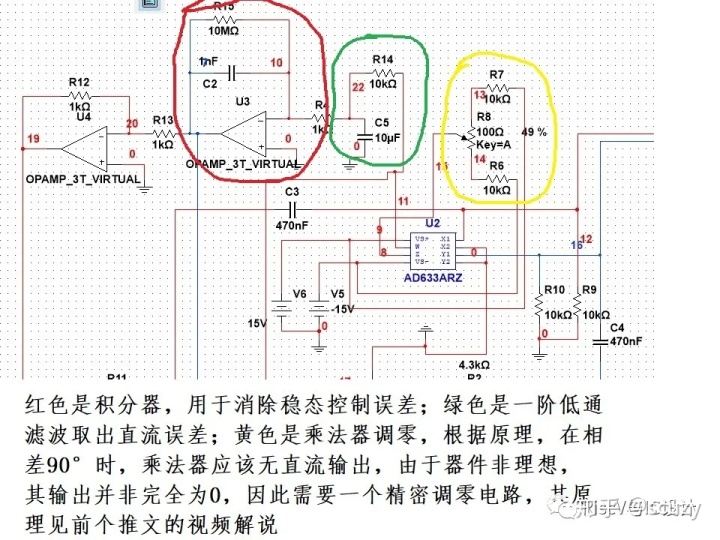
2)JFET可变电阻
jFET的输出电流ID与VGS(栅源电压)、VDS(漏源电压)关系如下,可以推导出其输出导纳gDS
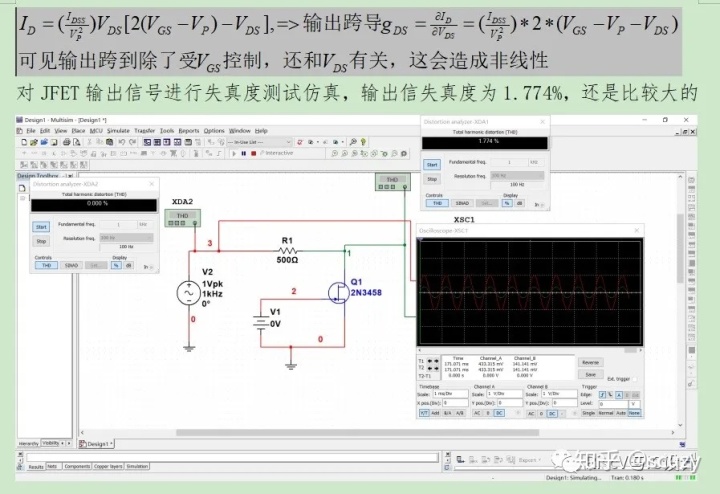
现在如下图所示,通过R3/R2引入对Vds信号的反馈,目的是减小JFET输出电阻的非线性,造成非线性的原因从上图的gDS公式可见其还是Vds的函数,因此我们的做法还是负反馈!引入对Vds信号的负反馈来抑制Vds对ID的影响!
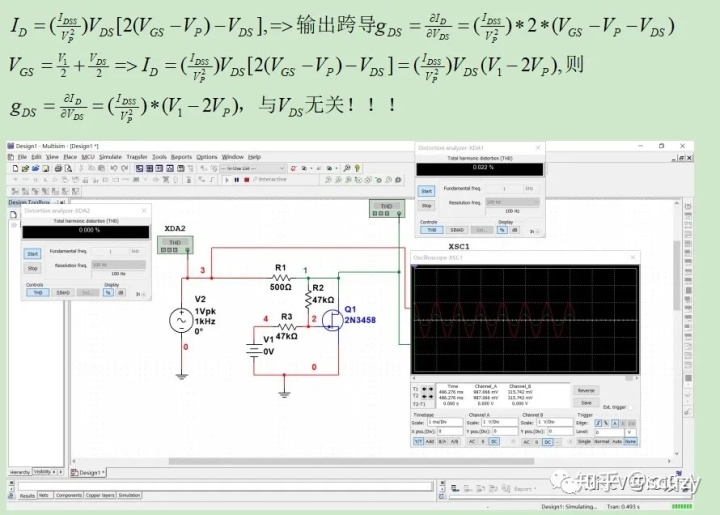
失真补偿以后,失真度降为0.022%,这改善非常明显,记住善于应用负反馈者,如果模拟电路世界的天下一分为四,你已得其一!是不是有点当年诸葛大神的隆中对三分天下的意思?
这种JFET低失真可变电阻很有用,例如下图的低失真系数的正弦波振荡器:
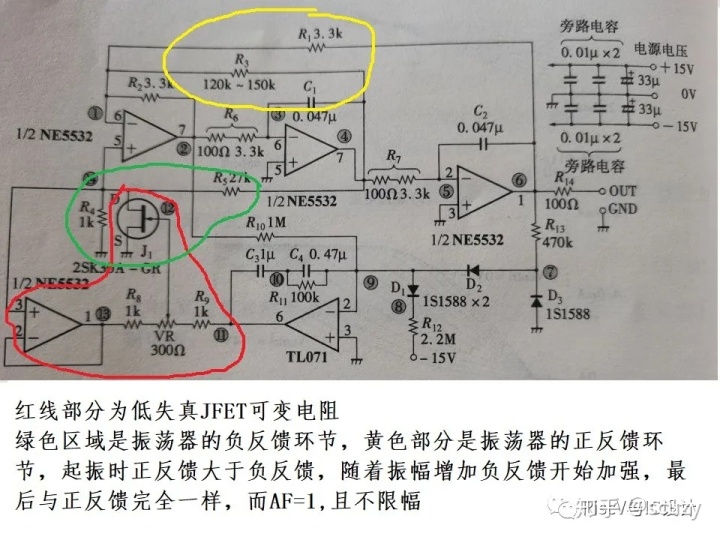
红色区域左下角的1:1运放就是为了隔离R8/R9/VR对R4的负载效应; TL071也是反馈控制中的积分环节,目的一样是消除稳态误差;D2/D3构成主要的信号幅度信息提取网络,采用半波整流电路取出正半周信号,通过积分器其实就是半波整流输出信号的平均直流分量,该分量与正弦波的幅度成比例:
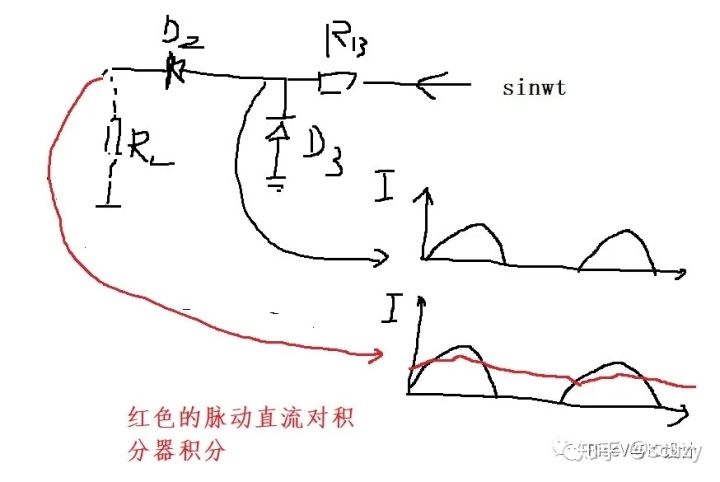
二极管半波整流虽然简单而且不精确,但是和积分器搭配却是很常见的信号幅度提取与反馈控制的手段!
关注微信公众号: RiscV与IC设计

修改成小时分钟_银行核心系统24小时机制实现总结)




SVD推荐(1)解读奇异值分解)








)



