清北学堂培训2019.4.4

第一次培训，心情有点激动（尽管没了清明节），还见到了各地的dalao们，十分开森

Day 1（李昊dalao）

上午篇

上午呢，主要讲了关于高精，快速幂，膜模意义下的运算，筛素数，费马小定理以及欧拉定理，欧拉函数。。。

我印象最深刻的，便是dalao的c++必备head（头文件及各种令人窒息的define）

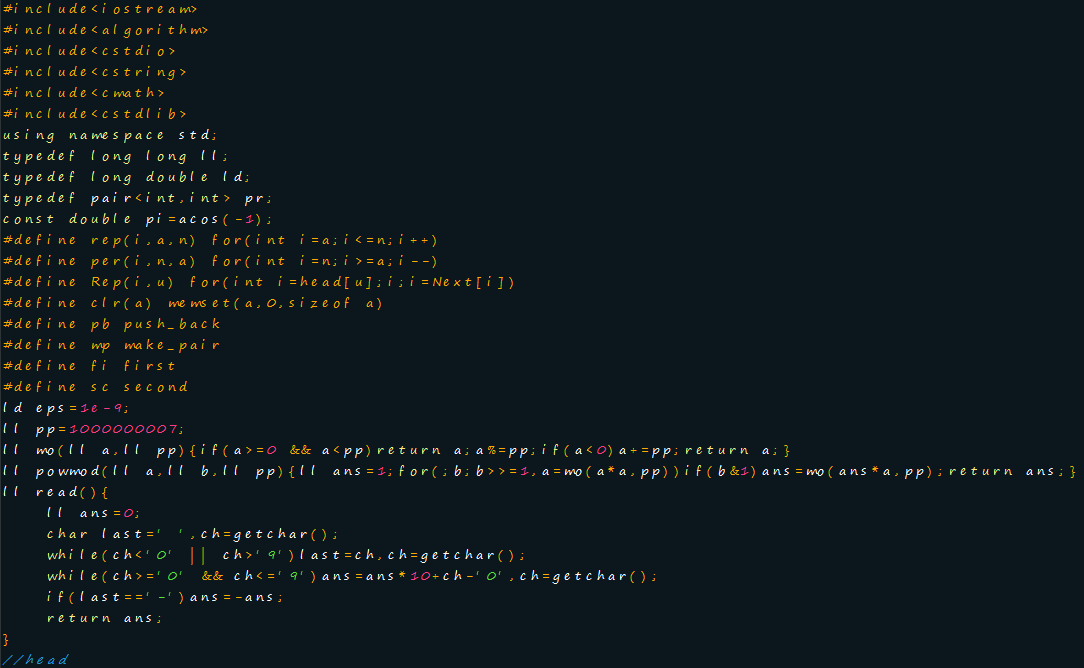
让人头脑一热QAQ

高精度（先全部考虑非负数）

高精度主要分为以下几个部分

1.高精度加法:

思路：模拟竖式运算

注意：进位

优化：压位

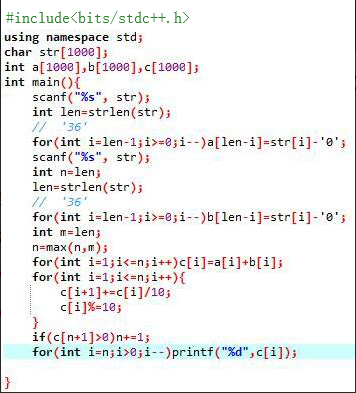
2.高精度减法：

思路：同加法相似，模拟竖式运算，进位变为退位

注意：结果为负数的情况

3.高精乘

思路：类似，模拟竖式运算，考虑进位

注意：结果为0的情况

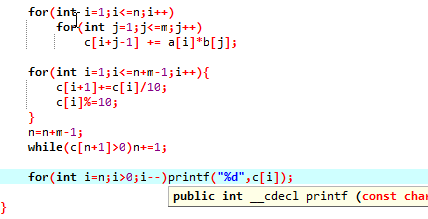
4.高精除以单精（高精除以高精在日常并不常用）

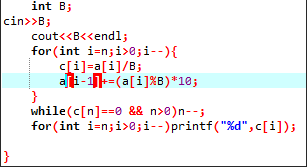
至于负数的情况呢QAQ

加法：

•一个数是负数：变为减法

•两个数是负数：全部变为正数算加法，最后取负

减法：

•被减数是负数：全部变为正数算加法，最后取负

•减数是负数：减数取负，变为加法

•都是负数：都取负，变为减法，即（-减数）-（-被减数）

乘法：

•统计负数个数s

•都变为非负数计算，若s为奇数，最后取负

除法同理。。。

膜模意义下的运算

这一个就听得十分有意思（毕竟我提前了解了一下）

这里需注意：无除法运算（很容易遗忘）

性质：

•满足基本的交换律、分配率、结合律

•对中间结果取模不影响最终答案

快速幂：

1.分治

int calc(int a,int b,int c)
{if(b==1){return a;}int tmp=calc(a,b/2,c);tmp=tmp*tmp%c;if(b&1){tmp=tmp*a%c;}return tmp;
}

2.快速幂

int ans=1;
while(b)
{if(b&1){ans=ans*a%c;}a=a*a%c;b/=2;
}

类似于这样的操作

费马小定理/欧拉定理

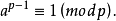
在模意义下有这个东西：

•C(n, m) = n! / ( (n-m)! * m! )

• = n! * ( (n-m)! * m! )^(p-2)

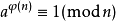
显然二者有推广关系

筛法

前面讲过，这里就不一一赘述

欧拉函数

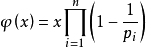
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> pr;
const double pi=acos(-1);
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define Rep(i,u) for(int i=head[u];i;i=Next[i])
#define clr(a) memset(a,0,sizeof a)
#define pb push_back
#define mp make_pair
#define fi first
#define sc second
ld eps=1e-9;
ll pp=1000000007;
ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;}
ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;}
ll read(){ll ans=0;char last=' ',ch=getchar();while(ch<'0' || ch>'9')last=ch,ch=getchar();while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();if(last=='-')ans=-ans;return ans;
}
//head
#define N 110000
bool p[N];
int prime[N],tot=0,rec[N],phi[N];
int main(){clr(p);rep(i,2,100000){if(!p[i]){prime[++tot]=i;rec[i]=i;}for(int j=1;j<=tot && prime[j]*i<=100000;j++){p[prime[j]*i]=1;rec[prime[j]*i]=prime[j];if(i%prime[j]==0)break;}}rep(i,2,100000)if(rec[i]==i)phi[i]=i-1;elseif(i%(rec[i]*rec[i])==0)phi[i]=phi[i/rec[i]]*rec[i];else phi[i]=phi[i/rec[i]]*(rec[i]-1);rep(i,2,20)printf("%d : %d\n",i,phi[i]);
}

李昊大佬的码风有些清奇qwq

下午篇

蒟矩阵

such as：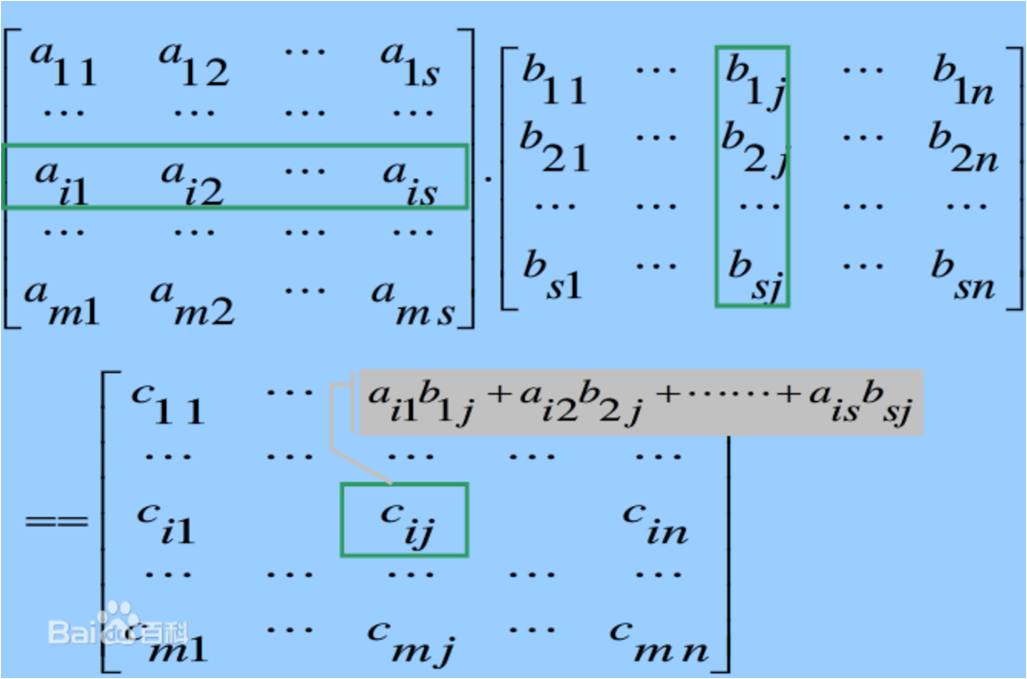

特殊矩阵：

1.上三角矩阵

2.分块矩阵

3.对角矩阵

4.对称矩阵

行列式

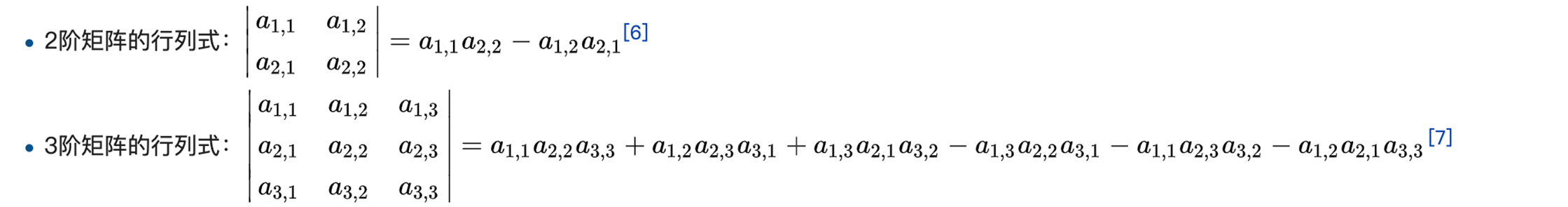
需要学一下逆序对（皮一下很舒服）

可以学一下这本书@工程数学线性代数

矩阵逆元

说到逆元，以下是洛谷P3811求乘法逆元的正解

#include<bits/stdc++.h>
using namespace std;
int n,p,inv[25000528];
int main()
{scanf("%d%d",&n,&p);inv[1]=1;for(int i=2;i<=n;i++){inv[i]=(long long)(p-p/i)*inv[p%i]%p;    }for(int i=1;i<=n;i++){printf("%d\n",inv[i]);}return 0;
}