骨牌铺方格
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 46495 Accepted Submission(s): 22470
Problem Description
在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数.
例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图:
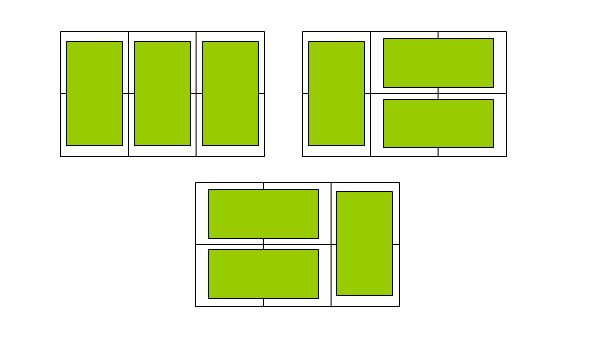
例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图:

Input
输入数据由多行组成,每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0<n<=50)。
Output
对于每个测试实例,请输出铺放方案的总数,每个实例的输出占一行。
Sample Input
1 3 2
Sample Output
1 3 2
#include<stdio.h>
int sum(int a)
{if(a==1)return 1;if(a==2)return 2;if(a>2){return sum(a-1)+sum(a-2);}
}int main()
{__int64 a;int n;while(~scanf("%d",&n)&&n<=50){a=sum(n);printf("%I64d\n",a);a=0;}return 0;}这个使用循环做法,但是实践过程中发现运行速度太慢,不建议使用。
#include <stdio.h>
int main()
{int n,j;__int64 a[51];while(scanf("%d",&n)!=EOF){a[1]=1;a[2]=2;for(j=3;j<=n;j++)a[j]=a[j-1]+a[j-2];printf("%I64d\n",a[n]);}
}
然后发现用数组做速度快了好多,省下了好多递归调用的时间,所以快很多。
这个题的思路是
1)先铺好n-1个格,有f(n-1)个方法,再铺第n层的时候只有一种方法,所以总方法是1*f(n-1);
2)先铺好n-2格,有f(n-2)个方法,再铺后面两层的时候只能两个都竖着铺(否则与第一种情况重复),所以也只有一种情况,总方法数是1*f(n-2)
推出f(n)=f(n-1)+f(n-2)











)


(转))

)


