1.遗传算法简介
遗传算法是一种基于自然选择和群体遗传机理的搜索算法,它模拟了自然选择和自然遗传过程中的繁殖、杂交和突变现象.再利用遗传算法求解问题时,问题的每一个可能解都被编码成一个“染色体”,即个体,若干个个体构成了群体(所有可能解).在遗传算法开始时,总是随机的产生一些个体(即初始解),根据预定的目标函数对每一个个体进行评估,给出一个适应度值,基于此适应度值,选择一些个体用来产生下一代,选择操作体现了“适者生存”的原理,“好”的个体被用来产生下一代,“坏”的个体则被淘汰,然后选择出来的个体,经过交叉和变异算子进行再组合生成新的一代,这一代的个体由于继承了上一代的一些优良性状,因而在性能上要优于上一代,这样逐步朝着最优解的方向进化.因此,遗传算法可以看成是一个由可行解组成的群体初步进化的过程.
2.遗传算法原理简析
2.1.GA算法是一种元启发式自然选择的过程 ,遗传算法通常是利用生物启发算子,如变异、交叉和选择来生成高质量的优化和搜索问题的解决方案。
借鉴生物进化理论,遗传算法将问题模拟成一个生物进化过程,通过遗传、交叉、突变、自然选择等操作产生下一代的解,并逐步淘汰适应度函数值低的解,增加适应度函数高的解。这样进化N代后就很有 可能会进化出适应度函数值很高的个体。
2.2.遗传算法的基本术语
个体:可行解
种群:可行解集
染色体:可行解的编码
基因:可行解的分量
基因形式:遗传编码
适应度:适应度函数(评价的值)
选择:选择操作
交叉:编码的交叉操作
变异:可行解码的变异
3.遗传算法的基本操作
遗传算法的操作即模拟生物基因操作:优选适应性强的个体的“选择”;个体间交换基因产生新个体的“交叉”;个体间的基因突变而产生新个体的“变异”。
3.1选择
选择是指从群体中选择优良个体并淘汰劣质个体的操作.它建立在适应度评估的基础上.适应度越大的个体,被选中上的可能性就越大,他的“子孙”在下一代中的个数就越多,选择出来的个体就被放入配对库中.目前常用的选择方法有轮赌盘方法、最佳个体保留法、期望值法、排序选择法、竞争法、线性标准化法.
3.2交叉
交叉就是指把两个父代个体的部分结构加以替换重组而生成新的个体的操作,交叉的目的是为了在下一代产生新的个体,通过交叉操作,遗传算法的搜索能力得到了飞跃性的提高.交叉是遗传算法获取优良个体的重要手段.交叉操作是按照一定的交叉概率在匹配库中随机的选取两个个体进行的,交叉位置也是随机的,交叉概率一般取得很大,为0.6~0.9.
3.3变异
变异就是以很小的变异概率Pm随机地改变种群中个体的某些基因的值,变异操作的基本过程是:产生一个[0,1]之间的随机数rand,如果rand0.5,遗传算法就退化为了随机搜索.
https://blog.csdn.net/jzp1083462154/article/details/80032987
4.遗传算法的操作步骤
开始循环直至找到满意的解。
1.评估每条染色体所对应个体的适应度。
2.遵照适应度越高,选择概率越大的原则,从种群中选择两个个体作为父方和母方。
3.抽取父母双方的染色体,进行交叉,产生子代。
4.对子代的染色体进行变异。
5.重复2,3,4步骤,直到新种群的产生
结束循环
流程图参照老师上课PPT讲解过的内容,这里就不再贴出。
5.遗传算法的实现
遗传算法优化方法:
(1)精英主义(Elitist Strategy)选择:是基本遗传算法的一种优化。为了防止进化过程中产生的最优解被交叉和变异所破坏,可以将每一代中的最优解原封不动的复制到下一代中。
(2)插入操作:可在3个基本操作的基础上增加一个插入操作。插入操作将染色体中的某个随机的片段移位到另一个随机的位置。
求解一个目标函数y=sin(10 *Π *x)/x
部分代码:
运行结果
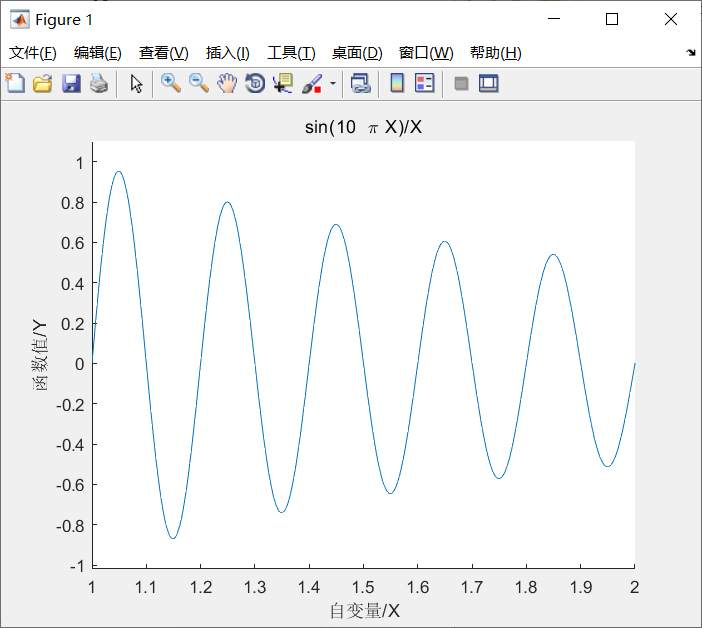
6.遗传算法的特点
①遗传算法是对参数的编码进行操作,而非对参数本身。
②遗传算法是从许多点开始并行操作,并非局限于一点,从而可有效防止搜索过程收敛于局部最优解。
③遗传算法通过目标函数计算适值,并不需要其它推导和附加信息,因而对问题的依赖性较小。
④遗传算法的寻优规则是由概率决定的,而非确定性的。
⑤遗传算法在解空间进行高效启发式搜索,而非盲目地穷举或完全随机搜索。
⑥遗传算法对所求解的优化问题没有太多的数学要求。
⑦遗传算法具有并行计算的特点,因而可通过大规模并行计算来提高计算速度
。
7.总结
由于对算法的运用掌握的不是很熟练,多目标求解代码还没运行出来,给大家提供一个概念理解的参考链接:https://www.cnblogs.com/lomper/p/3831428.html
计算智能这门课还需要多多熟悉matlab软件,发现这位博主讲解的挺仔细:https://blog.csdn.net/zhazhazl/article/details/52192595?tdsourcetag=s_pctim_aiomsg
另外这位博主讲解的算法分析很不错:https://blog.csdn.net/u010451580/article/details/51178225
本文参考:
https://blog.csdn.net/sinat_38321889/article/details/79001599?tdsourcetag=s_pctim_aiomsg







)




...)






