相信大家在小学奥数中都遇到这样一个问题：4条直线最多能将平面分成几部分？这个问题并不能难倒我们，但是如果将问题改为：4个平面最多能将空间分为几部分？这下子我们可能就要放弃了。

为了解决这个问题，今天我们就来研究一组相关的问题，这些问题的解决方案都涉及数学归纳法。

问题1 : 个点最多能将一条直线分为多少个区域?

1个点：

2个点：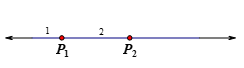

3个点：

点数	1	2	3	...	个点
区域数	2	3	4	...

从表中我们容易猜想得出，个点最多能将一条直线分为个区域。为了表述方便，令

直线上个点所决定的直线上区域的最大个数

当一个额外的点被添加到这条直线上会发生什么呢？

我们观察一下：每次一个新的点被添加到这条直线上，它必须被插入到由之前的点决定的一个现有的区域中。因此，该区域被划分为两个区域和，而之前的所有其他区域保持不变。因此，当向直线添加一个新点时，只添加一个新区域。

因此我们得到一个循环关系：

这样，我们可以推导出显性公式：

接下来我们使用数学归纳法进行证明。

设命题:

• 基步：，因此真。
• 归纳步：假设真，即对成立。通过递推关系有 也成立。

因此根据数学归纳法，对所有成立。

问题2 : 条直线最多能将一个平面分为多少个区域?

1条直线：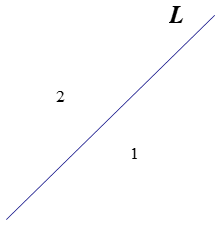

2条直线：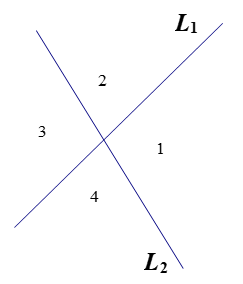

3条直线：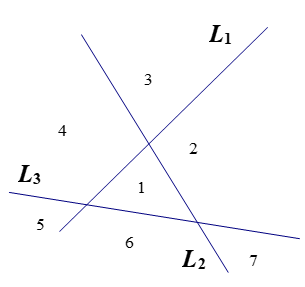

4条直线：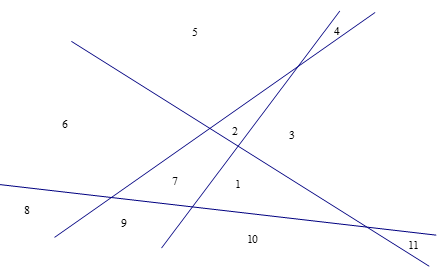

类似地，令

平面上条直线所决定的平面上区域的最大个数我们已经观察到，如果是平面上条直线所确定的平面上的最大区域数，则，，，。

直线数 n	1	2	3	4	5	6	7
区域数	2	4	7	11

我们可以用同样的方法求出，等等，但是这些图越来越难构造。因此我们需要找到这个序列的显性公式。我们可以采用有限差分法来构造这个序列的显性公式，注意到第二排差值是1，2，3，4，第一排差值是1，1，1。因为第一排差值是常数，我们期望可能是的二次函数。令

其中、、为常数，可由上表中的部分数据确定。然后，使用表中的值(列一个三元一次方程组)，解得因此，对于的显性公式的一个猜想是我们来看看如果5条直线的情况。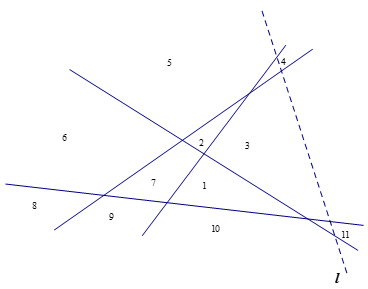

因为不平行于任何其他直线，也不经过其他直线任何较早的交点，所以每次与现有直线相交时，它就把它所经过的区域分成两个区域。当经过第四条直线后，又将最后一个区域划分为两个区域。简言之，第5条直线产生了5个新区域。同样的论证表明，将第条线添加到n条线的组合中会产生个新区域。我们可以把它表示为一个递归关系：

同样地，我们可以用数学归纳法证明显性公式成立，这里不再赘述。

问题3 : 空间中个平面最多划分多少个区域?

令

空间中个平面所决定的最大区域数观察上图可得，，。但是你可能会发现用图来表示的情况很困难，因为图很复杂。

想象一下在三个平面的图形中添加第四个平面的结果。给定三个平面都会与新平面有一条交线，三条直线最多能将平面分为7个区域。因此，再使用有限差分法(列一个四元一次方程组)来构造序列的显性公式:

现在尝试联系问题1、2、3

我们看下表：

元素个数	分割直线数	分割平面数	分割空间数
0	1	1	1
1	2	2	2
2	3	4	4
3	4	7	8
4	5	11	15
...	...	...	...
条直线	个

注意到，在表格中

对所有自然数成立。

这样我们就解决了最开始提出的问题。

参考文献[1]G.波利亚.数学与猜想:数学中的归纳和类比(第1卷)[M].科学出版社，2001.

【往期回顾】

• 图解数学

图解装错信封问题

人人都能看懂的美妙证明！图解柏拉图多面体和欧拉公式

在纸上投针就能算出圆周率π？图解蒲丰投针实验

什么是数列的极限？图解ε-N语言

• 数学文化：

原来数学还可以这样！

• 生活中的数学：

找东西背后的概率问题

一局俄罗斯方块可以一直玩下去吗？

• 公式之美：

你还在死记自然数平方和的公式吗？那你就not fashion了！

最短的证明有多短！？

最短的证明有多短！？(二)

喜欢就点亮在看，谢谢支持