混淆矩阵的精度计算公式为:精度=(TP+TN)/(TP+TN+FP+FN),也就是说,精度就是指正确的预测数目除以所有样本的数量。
准确率、召回率与f-分数:总结混淆矩阵还有几种方法,其中最常见的就是准确率和召回率。准确率度量的是被预测为正例的样本有多少是整整的样例。即:准确率=TP/(TP+FP)。如果目标是限制假正例的数量,那么可以使用准确率作为性能目标。
召回率:召回率(recalll)度量的是正类样本中有多少被预测为正类,即:召回率=TP/(TP+FN),如果我们需要找出所有的正类样本,即避免反例是很重要的情况下,那么可以使用召回率作为性能指标。
在优化召回率与优化准确率之间需要折中,如果你预测所有样本都属于正类,那么可以轻松得到完美的召回率(没有假反例、也没有真反例)。但是,将所有样本都预测为正类,将会得得很多假正例,因此准确率会很低。与之相反,如果你的模型只讲一个最确定的数据点预测为正类,其他点都预测为反类,那么准确率将会很完美(假设这个数据点上实际上就属于正类),但是召回率会很差。(当然,准确率和召回率只是度量混淆矩阵情况中两个量,其他的可以根据实际情况取对应的参数)。
f-分数:虽然准确率和召回率是非常重要的度量,三式仅查看二者之一无法提供完美的途径,所以还有一种将两种方法汇总的方法——f-分数。它是准确率与召回率的调和平均,即:F=2*(准确率*召回率)/(准确率+召回率)。
由于f-分数同时考虑了准确率和召回率,所以它对于不平衡的二分类数据集来说是一种比精度更好的度量方式。我们对前面提到过的“9与其余”的数据集的预测结果计算f1-分数(我们这里假设“9”是正类,标记为True,其他样本为False):
from sklearn.metrics import f1_score
print("F1 score most frequent: {:.2f}".format(f1_score(y_test, pred_most_frequent)))
print("F1 score dummy: {:.2f}".format(f1_score(y_test, pred_dummy)))
print("F1 score logreg: {:.2f}".format(f1_score(y_test, pred_logreg)))
print("F1 score of Tree: {:.2f}".format(f1_score(y_test, pred_tree)))
运行后其结果如下:
F1 score most frequent: 0.00
F1 score dummy: 0.13
F1 score logreg: 0.89
F1 score of Tree: 0.55
由运行结果可以看出:most_frequency的预测中得到的是一条错误信息;另外需要注意的是,虚拟预测和决策树预测之间还是有差别的,尽管精度差别不大,但是f-分数却相差很大。在这里,f-分数更加符合我们对模型的直觉。f-分数的缺点则是比精度更加难以解释。
如果我们要对准确率、召回率和f1-分数做一个更加全面的总结,则可以使用classification_report这个函数,它可以同时计算这三个值,并以美观的形式打印出来。
from sklearn.metrics import classification_report
print("Most frequency class precious:")
print(classification_report(y_test, pred_most_frequent, target_names=["not Nine", "Nine"]))
print("Dummy model precious:")
print(classification_report(y_test, pred_dummy, target_names=["not Nine", "Nine"]))
print("Decision tree precious:")
print(classification_report(y_test, pred_tree, target_names=["not Nine", "Nine"]))
print("logistic regression precious")
print(classification_report(y_test, pred_logreg, target_names=["not Nine", "Nine"]))
运行结果如下图:
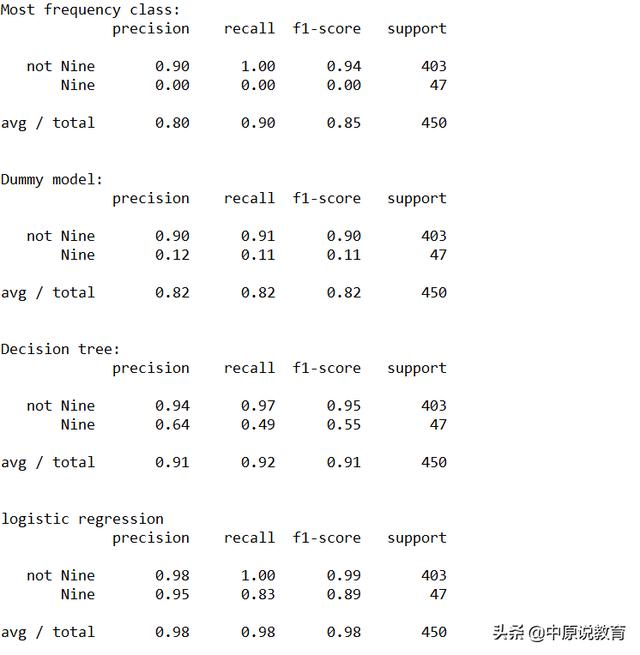
classification_report 属性打印
classification_report函数为每个类别(这里是True和False)生成一行,并给出以该类并为正类的准确率、召回率及f-分数。这里的最后一列support(支持)表示的是在这个类别中真实样本的数量;最后一行显示的是对应指标的加权平均(按每个类别中的样本个数加权)。
同时,我们从运行结果中还可以看出,虚拟模型与logreg之间的区别并不是很明显,选择哪个类作为正类对指标有很大影响。在这里选择Nine作为正类时logisticregression比其他方法更具备优势。



















