TVM：使用Tensor Expression (TE)来处理算子

在本教程中，我们将聚焦于在 TVM 中使用张量表达式（TE）来定义张量计算和实现循环优化。TE用纯函数语言描述张量计算（即每个表达式都没有副作用）。当在 TVM 的整体上下文中查看时，Relay 将计算描述为一组算子，并且其中每一个算子都可以表示为 TE 表达式，每个 TE 表达式获取输入张量并生成输出张量。
本文是TVM中 TE 语言的入门教程。TVM 使用领域专用（domain specific）的张量表达式来高效地构造内核。我们以两个使用 TE 语言的为例来演示基本工作流。第一个示例介绍了 TE 和带有向量加法的 schedule。第二个示例通过逐步优化矩阵与 TE 的乘法来扩展这些概念。这个矩阵乘法示例将作为未来涵盖更高级的 TVM 特性的教程的对比基础。

示例一：使用TE为CPU编写和调度向量加法

初始化 tvm环境

我们的第一个例子是使用 Python 来为向量加法实现一个 TE，然后是一个针对 CPU 的 schedule，我们从初始化 tvm 环境开始：

import tvm
import tvm.testing
from tvm import te
import numpy as np# 如果能够指定目标 CPU，那么将会得到更好地性能
# 如果用的是llvm，可以通过 `llc --version` 来查看 CPU 类型
# 可以通过查看 /proc/cpuinfo 来查看你的处理器可能支持的其他扩展，
# 比如，如果你的 CPU 有 AVX-512 指令集，那么你可以使用 `llvm -mcpu=skylake-avx512` 选项tgt = tvm.target.Target(target="llvm", host="llvm")

描述向量计算

我们首先描述向量加法计算。TVM 采用张量语义，每个中间结果表示为一个多维数组。我们需要描述规则来得到张量。我们首先定义一个符号变量 n 来表示形状。然后我们定义两个 placeholder 张量：A、B，它们的形状是 (n,)。然后我们通过一个 compute 操作，得到结果张量 C。compute 定义了一种计算，其输出符合指定的张量形状，并在由 lambda 函数定义的张量中的每个位置执行计算。注意，虽然 n 是一个变量，但它定义了A、B 和 C 张量之间的一致形状。请注意，在这个阶段没有实际的计算发生，因为我们只是声明应该如何进行计算。

n = te.var("n")
A = te.placeholder((n,), name="A")
B = te.placeholder((n,), name="B")
C = te.compute(A.shape, lambda i: A[i] + B[i], name="C")

注意：Lambda函数

te.compute方法的第二个参数是执行计算的函数。在本例中，我们使用一个匿名函数（也称为lambda函数）来定义计算，在本例中是对 a 和 B 的第 i 个元素的加法。

为计算创建一个默认的Schedule

虽然上面几行描述了计算规则，但我们可以用许多不同的方法计算 C 以适应不同的设备。对于具有多个 axis 的张量，您可以选择首先迭代哪个 axis ，另外计算可以跨不同的线程拆分。TVM要求用户提供一个 schedule，来描述应如何执行计算。TE 中的 schedule 操作可以更改循环顺序、跨不同线程拆分计算、将数据块分组在一起，以及其他操作。schedule 背后的一个重要概念是，它们只描述如何执行计算，因此相同 TE 的不同 schedule 一定会产生相同的结果。

在 TVM 中，我们可以创建一种朴素的 schedule ，按照行优先的顺序来计算 C。

for (int i = 0; i < n; ++i) {C[i] = A[i] + B[i];
}

s = te.create_schedule(C.op)

编译并验证默认的 schedule

通过 TE 表达式和 schedule，我们可以为目标语言和体系结构生成可运行的代码，在本例中是 LLVM 和 CPU 。我们向 TVM 提供 schedule、schedule 中的TE表达式列表、目标和主机，以及我们正在生成的函数的名称。输出的结果是可以直接从 Python 调用 type-erased 函数。

在下一行中，我们使用 tvm.build 创建一个函数。build 函数接受 schedule、函数所需的签名（包括输入和输出）以及我们要编译到的目标语言。

fadd = tvm.build(s, [A, B, C], tgt, name="myadd")

我们运行该函数，并将输出与 numpy 中的相同计算进行比较。编译后的 TVM 函数提供了一个简明的C API，可以被任何语言调用。我们首先创建一个设备（在本例中为CPU），这是一个 TVM 可以编译 schedule 的设备。在本例中，设备是LLVM CPU target。然后，我们可以在设备中初始化张量并执行自定义的加法操作。为了验证计算的正确性，我们可以将c张量的输出结果与 numpy 执行的相同计算进行比较。

dev = tvm.device(tgt.kind.name, 0)n = 1024
a = tvm.nd.array(np.random.uniform(size=n).astype(A.dtype), dev)
b = tvm.nd.array(np.random.uniform(size=n).astype(B.dtype), dev)
c = tvm.nd.array(np.zeros(n, dtype=C.dtype), dev)
fadd(a, b, c)
tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())

为了对比这个朴素版本的自定义向量加法与 numpy 的速度差异，创建一个辅助函数来运行 TVM 生成代码的 profile。

import timeitnp_repeat = 100
np_running_time = timeit.timeit(setup="import numpy\n""n = 32768\n"'dtype = "float32"\n'"a = numpy.random.rand(n, 1).astype(dtype)\n""b = numpy.random.rand(n, 1).astype(dtype)\n",stmt="answer = a + b",number=np_repeat,
)
print("Numpy running time: %f" % (np_running_time / np_repeat))def evaluate_addition(func, target, optimization, log):dev = tvm.device(target.kind.name, 0)n = 32768a = tvm.nd.array(np.random.uniform(size=n).astype(A.dtype), dev)b = tvm.nd.array(np.random.uniform(size=n).astype(B.dtype), dev)c = tvm.nd.array(np.zeros(n, dtype=C.dtype), dev)evaluator = func.time_evaluator(func.entry_name, dev, number=10)mean_time = evaluator(a, b, c).meanprint("%s: %f" % (optimization, mean_time))log.append((optimization, mean_time))log = [("numpy", np_running_time / np_repeat)]
evaluate_addition(fadd, tgt, "naive", log=log)

此处输出：

Numpy running time: 0.000008
naive: 0.000006

使用并行性（paralleism）来优化 schedule

我们已经说明了 TE 的基本原理，现在让我们更深入地了解 schedule 的作用，以及它们如何用于优化不同体系结构的张量表达式。schedule 是应用于表达式的一系列步骤，用于以多种不同方式对其进行转换。当一个 schedule 应用于TE中的一个表达式时，输入和输出保持不变，但在编译时，表达式的实现可能会改变。在默认 schedule 中，这个张量加法是串行运行的，但该操作其实是很容易在所有处理器线程之间并行。我们可以将我们的操作并行调度到计算中：

s[C].parallel(C.op.axis[0])

tvm.lower 命令将生成 TE 的中间表示（IR）以及相应的 schedule 。通过在执行不同的 schedule 操作时 lowing 表达式，我们可以看到 schedule 对计算顺序的影响。我们使用标志 simple_mode=True 返回可读的 C 风格语句。

print(tvm.lower(s, [A, B, C], simple_mode=True))

此处输出：

primfn(A_1: handle, B_1: handle, C_1: handle) -> ()attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}buffers = {C: Buffer(C_2: Pointer(float32), float32, [n: int32], [stride: int32], type="auto"),A: Buffer(A_2: Pointer(float32), float32, [n], [stride_1: int32], type="auto"),B: Buffer(B_2: Pointer(float32), float32, [n], [stride_2: int32], type="auto")}buffer_map = {A_1: A, B_1: B, C_1: C} {for (i: int32, 0, n) "parallel" {C_2[(i*stride)] = ((float32*)A_2[(i*stride_1)] + (float32*)B_2[(i*stride_2)])}
}

TVM现在可以在独立的线程上运行这些块。我们在执行并行操作的情况下编译并运行这个新的 schedule：

fadd_parallel = tvm.build(s, [A, B, C], tgt, name="myadd_parallel")
fadd_parallel(a, b, c)tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())evaluate_addition(fadd_parallel, tgt, "parallel", log=log)

此处输出：

parallel: 0.000005

使用矢量化（vectorization）来优化 schedule

现代 CPU 能够对浮点数进行 SIMD 操作，我们可以对计算表达式使用另一个 schedule 来利用这一点。实现这一点需要多个步骤：首先，我们必须使用 split scheduling 原语将 schedule 拆分为内部循环和外部循环。内部循环可以使用向量化来使用使用向量化调度原语的 SIMD 指令，然后外部循环可以使用并行调度原语进行并行化。选择分割因子作为CPU上的线程数。

注：SIMD，全称 Single Instruction Multiple Data，单指令多数据流，能够复制多个操作数，并把它们打包在大型寄存器的一组指令集。

# 由于我们需要修改之前例子中的并行操作，因此这里要重建 schedule
n = te.var("n")
A = te.placeholder((n,), name="A")
B = te.placeholder((n,), name="B")
C = te.compute(A.shape, lambda i: A[i] + B[i], name="C")s = te.create_schedule(C.op)# factor 的选择需要适合你的线程数，这取决于架构，
# 建议将此系数设置为等于可用CPU核心数。
factor = 4outer, inner = s[C].split(C.op.axis[0], factor=factor)
s[C].parallel(outer)
s[C].vectorize(inner)fadd_vector = tvm.build(s, [A, B, C], tgt, name="myadd_parallel")evaluate_addition(fadd_vector, tgt, "vector", log=log)print(tvm.lower(s, [A, B, C], simple_mode=True))

此处输出：

vector: 0.000016
primfn(A_1: handle, B_1: handle, C_1: handle) -> ()attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}buffers = {A: Buffer(A_2: Pointer(float32), float32, [n: int32], [stride: int32], type="auto"),C: Buffer(C_2: Pointer(float32), float32, [n], [stride_1: int32], type="auto"),B: Buffer(B_2: Pointer(float32), float32, [n], [stride_2: int32], type="auto")}buffer_map = {A_1: A, B_1: B, C_1: C} {for (i.outer: int32, 0, floordiv((n + 3), 4)) "parallel" {for (i.inner.s: int32, 0, 4) {if @tir.likely((((i.outer*4) + i.inner.s) < n), dtype=bool) {C_2[(((i.outer*4) + i.inner.s)*stride_1)] = ((float32*)A_2[(((i.outer*4) + i.inner.s)*stride)] + (float32*)B_2[(((i.outer*4) + i.inner.s)*stride_2)])}}}
}

对比不同的 schedule

下面我们来对比以下之前提到的不同 schedule：

baseline = log[0][1]
print("%s\t%s\t%s" % ("Operator".rjust(20), "Timing".rjust(20), "Performance".rjust(20)))
for result in log:print("%s\t%s\t%s"% (result[0].rjust(20), str(result[1]).rjust(20), str(result[1] / baseline).rjust(20)))

此处输出：

Operator                  Timing             Performancenumpy    7.98278022557497e-06                     1.0naive              5.9189e-06      0.7414584684465222
parallel    4.9771999999999995e-06    0.6234920490550659vector    1.6127399999999997e-05    2.0202735819196875

注意：Code Specialization

代码专门化

正如我们所看到的，A、B 和 C 的声明都采用相同的形状参数 n。TVM将利用这一点，只向 kernel 传递一个 shape 参数，我们在打印的设备代码中找到它。这是专门化化的一种形式。

在 host 端，TVM 将自动生成检查代码，以检查参数中的约束。因此，如果将具有不同形状的数组传递到 fadd 中，将引发错误。

我们可以做更多的专门化。例如，我们可以在计算声明中写入n=tvm.runtime.convert（1024）而不是 n=te.var（“n”）。生成的函数将只获取长度为1024的向量。

我们已经定义、调度并编译了一个向量加法运算符，然后可以在 TVM Runtime 执行它。我们可以将算子保存为库，稍后可以使用 TVM Runtime 加载该库。

针对GPU的矩阵加法（可选）

在介绍保存与加载自定义算子库的方法之前，我们先来看一下如何针对 GPU 做矩阵加法。

TVM能够针对多种体系结构。在本例，我们将针对GPU中矢量加法的编译。

# 本段代码默认不运行，如果想要运行的话，请将 ``run_cuda = True``run_cuda = False
if run_cuda:# 这里的 target 需要根据自己的 GPU 类型修改：# NVIDIA：cuda# Radeon：rocm# OpenCL：opencltgt_gpu = tvm.target.Target(target="cuda", host="llvm")# 重建 schedulen = te.var("n")A = te.placeholder((n,), name="A")B = te.placeholder((n,), name="B")C = te.compute(A.shape, lambda i: A[i] + B[i], name="C")print(type(C))s = te.create_schedule(C.op)bx, tx = s[C].split(C.op.axis[0], factor=64)################################################################################# 最后，我们必须将迭代轴bx和tx绑定到GPU计算网格中的线程。# 朴素的 schedule 对GPU无效，这些是允许我们生成在GPU上运行的代码的特定构造。s[C].bind(bx, te.thread_axis("blockIdx.x"))s[C].bind(tx, te.thread_axis("threadIdx.x"))####################################################################### 编译# -----------# 在指定完 schdule 之后，我们可以将其编译成一个 TVM 函数。默认情况下，TVM编译成一个 type-erased 函 		# 数，可以从python端直接调用该函数。# 在下一行中，我们使用 tvm.build 来创建一个函数。build 函数采用 schedule、函数所需的签名（包括输如和输出）以及我们要编译到的目标语言。# 编译 fadd 的结果是一个GPU设备函数（如果涉及GPU）以及一个调用 GPU 函数的 host wrapper。fadd是生成的主机包装函数，它在内部包含对生成的设备函数的引用。fadd = tvm.build(s, [A, B, C], target=tgt_gpu, name="myadd")################################################################################# 编译过的 TVM 函数会有一个简洁的 C API，它可以被任意的语言调用## 我们提供一个 Python 的最小的数组 API 来帮助快速的测试和原型化# 该数组 API 是基于 `DLPack <https://github.com/dmlc/dlpack>`_ 标准.## - 我们首先创建一个 GPU 设备# - 然后 tvm.nd.array 从 GPU 拷贝数据# - ``fadd`` 运行真正的计算# - ``numpy()`` 从 GPU 数组拷贝回 CPU (这样我们就能验证正确性了).## 请注意，将数据复制到 GPU 上的内存和从中复制数据是必需的步骤。dev = tvm.device(tgt_gpu.kind.name, 0)n = 1024a = tvm.nd.array(np.random.uniform(size=n).astype(A.dtype), dev)b = tvm.nd.array(np.random.uniform(size=n).astype(B.dtype), dev)c = tvm.nd.array(np.zeros(n, dtype=C.dtype), dev)fadd(a, b, c)tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())################################################################################# 检查生成的 GPU 代码# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~# 我们可以检查在 TVM 中生成的代码，tvm.build 的结果是一个 TVM 模块。fadd 是一个 host 模块其中包含 		# host wrapper 的 host module，它同样包含一个CUDA（GPU）设备模块## 下面的代码取得设备模块并打印内容代码if (tgt_gpu.kind.name == "cuda"or tgt_gpu.kind.name == "rocm"or tgt_gpu.kind.name.startswith("opencl")):dev_module = fadd.imported_modules[0]print("-----GPU code-----")print(dev_module.get_source())else:print(fadd.get_source())

保存和加载编译过的模块

保存编译过的模块

除了运行时编译之外，我们还可以将编译后的模块保存到一个文件中，并在以后重新加载。下面的代码执行以下步骤：

它将编译后的主机模块保存到一个对象文件中。
然后将设备模块保存到 ptx 文件中。
cc.create_shared 调用编译器（gcc）来创建共享库

from tvm.contrib import cc
from tvm.contrib import utilstemp = utils.tempdir()
fadd.save(temp.relpath("myadd.o"))
if tgt.kind.name == "cuda":fadd.imported_modules[0].save(temp.relpath("myadd.ptx"))
if tgt.kind.name == "rocm":fadd.imported_modules[0].save(temp.relpath("myadd.hsaco"))
if tgt.kind.name.startswith("opencl"):fadd.imported_modules[0].save(temp.relpath("myadd.cl"))
cc.create_shared(temp.relpath("myadd.so"), [temp.relpath("myadd.o")])
print(temp.listdir())

此处输出：

['myadd.o', 'myadd.so']

注意：Module Storage Format

模块存储格式

CPU（Host）模块直接保存为共享库（.so）。设备代码可以有多种自定义格式。在我们的示例中，设备代码存储在 ptx 中，元数据在 json 文件中。它们可以通过导入单独加载和链接。

加载编译过的模块

我们可以从文件系统加载已编译的模块并运行代码。以下代码分别加载主机和设备模块，并将它们链接在一起。我们可以验证新加载的函数是否有效。

fadd1 = tvm.runtime.load_module(temp.relpath("myadd.so"))
if tgt.kind.name == "cuda":fadd1_dev = tvm.runtime.load_module(temp.relpath("myadd.ptx"))fadd1.import_module(fadd1_dev)if tgt.kind.name == "rocm":fadd1_dev = tvm.runtime.load_module(temp.relpath("myadd.hsaco"))fadd1.import_module(fadd1_dev)if tgt.kind.name.startswith("opencl"):fadd1_dev = tvm.runtime.load_module(temp.relpath("myadd.cl"))fadd1.import_module(fadd1_dev)fadd1(a, b, c)
tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())

将所有东西打包在一个库中

在上面的示例中，我们分别存储设备和主机代码。TVM 还支持将所有内容导出为一个共享库。在 hood 下，我们将设备模块打包成二进制blob，并将它们与主机代码链接在一起。目前我们支持Metal、OpenCL和CUDA模块的包装。

fadd.export_library(temp.relpath("myadd_pack.so"))
fadd2 = tvm.runtime.load_module(temp.relpath("myadd_pack.so"))
fadd2(a, b, c)
tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())

注意：Runtime API and Thread Safety

运行时API与线程安全

TVM 的编译模块并不依赖于 TVM 编译器。它们只依赖于最小 Runtime Library。TVM Runtime Library 包装设备驱动程序，并向编译函数提供线程安全和设备无关调用。

这意味着我们可以从任何GPU上的任何线程调用已编译的TVM函数，前提是您已经为该GPU编译了代码。

生成OpenCL代码

TVM 为多种后端提供代码生成功能。我们还可以生成在 CPU 后端上运行的 OpenCL 代码或 LLVM 代码。

下面的代码可以生成OpenCL代码，在OpenCL设备上创建数组，并验证代码的正确性。

if tgt.kind.name.startswith("opencl"):fadd_cl = tvm.build(s, [A, B, C], tgt, name="myadd")print("------opencl code------")print(fadd_cl.imported_modules[0].get_source())dev = tvm.cl(0)n = 1024a = tvm.nd.array(np.random.uniform(size=n).astype(A.dtype), dev)b = tvm.nd.array(np.random.uniform(size=n).astype(B.dtype), dev)c = tvm.nd.array(np.zeros(n, dtype=C.dtype), dev)fadd_cl(a, b, c)tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())

注意：TE Scheduling Primitives

TE 调度原语

TVM 包括许多不同的调度原语：
split：按定义的因子将指定轴拆分为两个轴。
tile：平铺将按定义的因子沿两个轴分割计算。
fuse：融合一次计算的两个连续轴。
reorder：可以将计算轴重新排序为定义的顺序。
bind：可以将计算绑定到特定线程，在GPU编程中很有用。
compute_at：默认情况下，TVM将在函数的最外层或根计算张量。compute_at指定应在另一个运算符的第一个计算轴上计算一个张量。
compute_inline：当标记为inline时，计算将展开，然后插入到需要张量的地址中。
compute_root：将计算移动到函数的最外层或根。这意味着，在进入下一个阶段之前，将对计算阶段进行完全计算。

可以在Schedule primitives 文档页面中找到这些原语的完整描述。

示例二：用TE手动优化矩阵乘

现在，我们将考虑第二个更高级一些的示例，演示如何用 18 行 Python 代码 TVM 加速一个共同的矩阵乘法运算 18倍。

矩阵乘法是一种计算密集型运算。要获得良好的CPU性能，有两个重要的优化：

提高内存访问的缓存命中率。高缓存命中率可以加速复杂的数值计算和热点内存访问。这要求我们将源内存访问模式转换为适合缓存策略的模式。
SIMD（单指令多数据），也称为矢量处理单元。在每个循环中，SIMD 都可以处理一小批数据，而不是处理单个值。这要求我们以统一模式转换循环体中的数据访问模式，以便LLVM 后端可以将其 lower 到 SIMD。

本教程中使用的技术是这个仓库中提到的技巧的一部分。其中一些已被 TVM 抽象自动使用，但由于 TVM 的一些约束，有一些无法自动使用。

准备工作和性能baseline

我们首先采集 numpy 实现的矩阵乘的数据：

import tvm
import tvm.testing
from tvm import te
import numpy# 矩阵的尺寸：
# (M, K) x (K, N)
# 你可以自己试一些不同的尺寸，有时候 TVM 的优化结果会好于含 MKL 的numpy
M = 1024
K = 1024
N = 1024# tvm 中默认的数据类型
dtype = "float32"# 与之前一样，这里可以根据自己的处理器及其是否支持某些指令集来改变 targettarget = tvm.target.Target(target="llvm", host="llvm")
dev = tvm.device(target.kind.name, 0)# 随机生成一些 tensor 用于测试
a = tvm.nd.array(numpy.random.rand(M, K).astype(dtype), dev)
b = tvm.nd.array(numpy.random.rand(K, N).astype(dtype), dev)# 重复实验，得到 numpy 的矩阵乘实现的 baseline
np_repeat = 100
np_running_time = timeit.timeit(setup="import numpy\n""M = " + str(M) + "\n""K = " + str(K) + "\n""N = " + str(N) + "\n"'dtype = "float32"\n'"a = numpy.random.rand(M, K).astype(dtype)\n""b = numpy.random.rand(K, N).astype(dtype)\n",stmt="answer = numpy.dot(a, b)",number=np_repeat,
)
print("Numpy running time: %f" % (np_running_time / np_repeat))answer = numpy.dot(a.numpy(), b.numpy())

此处输出：

Numpy running time: 0.009308

现在，我们用 TVM TE 编写一个基本矩阵乘法，并验证它产生的结果与numpy实现相同。我们还编写了一个函数，它将帮助我们度量进度优化的性能。

# 使用 TE 实现的 TVM 的矩阵乘
k = te.reduce_axis((0, K), "k")
A = te.placeholder((M, K), name="A")
B = te.placeholder((K, N), name="B")
C = te.compute((M, N), lambda x, y: te.sum(A[x, k] * B[k, y], axis=k), name="C")# 默认 schedule
s = te.create_schedule(C.op)
func = tvm.build(s, [A, B, C], target=target, name="mmult")c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), dev)
func(a, b, c)
tvm.testing.assert_allclose(c.numpy(), answer, rtol=1e-5)def evaluate_operation(s, vars, target, name, optimization, log):func = tvm.build(s, [A, B, C], target=target, name="mmult")assert funcc = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), dev)func(a, b, c)tvm.testing.assert_allclose(c.numpy(), answer, rtol=1e-5)evaluator = func.time_evaluator(func.entry_name, dev, number=10)mean_time = evaluator(a, b, c).meanprint("%s: %f" % (optimization, mean_time))log.append((optimization, mean_time))log = []evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="none", log=log)

此处输出：

none: 3.109406

让我们看一下使用 TVM lower 函数的算子和默认 schedule 的中间表示 IR。请注意，该实现本质上是矩阵乘法的简单实现，在 A 和 B 矩阵的索引上使用三个嵌套循环。

print(tvm.lower(s, [A, B, C], simple_mode=True))

此处输出：

primfn(A_1: handle, B_1: handle, C_1: handle) -> ()attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}buffers = {C: Buffer(C_2: Pointer(float32), float32, [1024, 1024], []),A: Buffer(A_2: Pointer(float32), float32, [1024, 1024], []),B: Buffer(B_2: Pointer(float32), float32, [1024, 1024], [])}buffer_map = {A_1: A, B_1: B, C_1: C} {for (x: int32, 0, 1024) {for (y: int32, 0, 1024) {C_2[((x*1024) + y)] = 0f32for (k: int32, 0, 1024) {C_2[((x*1024) + y)] = ((float32*)C_2[((x*1024) + y)] + ((float32*)A_2[((x*1024) + k)]*(float32*)B_2[((k*1024) + y)]))}}}
}

优化1：blocking阻塞

提高缓存命中率的一个重要技巧是阻塞，在这种情况下，我们可以构造内存访问，使块内部是具有高内存局部性的小邻域。在本教程中，我们选择块因子 32。这会使得一个块填充内存的 32*32*sizeof（float）区域。这对应于 4KB 的缓存大小，和一级缓存 32KB 的参考缓存大小。

我们首先为 C 操作创建一个默认的调度，然后使用指定的块因子对其应用一个 tile 调度原语，调度原语以向量 [x_-outer，y_-outer，x_-inner，y_-inner] 的形式返回从最外层到最内层的循环顺序。然后，我们得到操作输出的缩减轴，并使用因子4对其执行拆分操作。这个因素不会直接影响我们现在正在进行的阻塞优化，但在以后应用矢量化时会很有用。
现在操作已被阻塞，我们可以对计算进行重新排序，将简化操作放入计算的最外层循环中，从而帮助确保被阻塞的数据仍保留在缓存中。这就完成了 schedule，我们可以构建和测试与原始 schedule 相比的性能。

bn = 32# Blocking by loop tiling
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)# Hoist reduction domain outside the blocking loop
s[C].reorder(xo, yo, ko, ki, xi, yi)evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="blocking", log=log)

此处输出：

blocking: 0.291928

通过重新排序计算以利用缓存，我们可以看到计算性能的显著提高。现在，打印内部表示并将其与原始表示进行比较：

print(tvm.lower(s, [A, B, C], simple_mode=True))

此处输出：

primfn(A_1: handle, B_1: handle, C_1: handle) -> ()attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}buffers = {A: Buffer(A_2: Pointer(float32), float32, [1024, 1024], []),C: Buffer(C_2: Pointer(float32), float32, [1024, 1024], []),B: Buffer(B_2: Pointer(float32), float32, [1024, 1024], [])}buffer_map = {A_1: A, B_1: B, C_1: C} {for (x.outer: int32, 0, 32) {for (y.outer: int32, 0, 32) {for (x.inner.init: int32, 0, 32) {for (y.inner.init: int32, 0, 32) {C_2[((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)) + y.inner.init)] = 0f32}}for (k.outer: int32, 0, 256) {for (k.inner: int32, 0, 4) {for (x.inner: int32, 0, 32) {for (y.inner: int32, 0, 32) {C_2[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] = ((float32*)C_2[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] + ((float32*)A_2[((((x.outer*32768) + (x.inner*1024)) + (k.outer*4)) + k.inner)]*(float32*)B_2[((((k.outer*4096) + (k.inner*1024)) + (y.outer*32)) + y.inner)]))}}}}}}
}

优化2： vectorization矢量化

另一个重要的优化技巧是矢量化。当内存访问模式一致时，编译器可以检测到该模式并将连续内存传递给 SIMD 向量处理器。在TVM中，我们可以利用这个硬件特性，使用矢量化接口来提示编译器这个模式。

在本教程中，我们选择对内部循环行数据进行矢量化，因为它已经是我们之前优化中的缓存友好型数据。

# 应用矢量化的优化方式
s[C].vectorize(yi)evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="vectorization", log=log)# 矢量化之后生成的 IR
print(tvm.lower(s, [A, B, C], simple_mode=True))

此处输出：

vectorization: 0.331263
primfn(A_1: handle, B_1: handle, C_1: handle) -> ()attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}buffers = {C: Buffer(C_2: Pointer(float32), float32, [1024, 1024], []),A: Buffer(A_2: Pointer(float32), float32, [1024, 1024], []),B: Buffer(B_2: Pointer(float32), float32, [1024, 1024], [])}buffer_map = {A_1: A, B_1: B, C_1: C} {for (x.outer: int32, 0, 32) {for (y.outer: int32, 0, 32) {for (x.inner.init: int32, 0, 32) {C_2[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = broadcast(0f32, 32)}for (k.outer: int32, 0, 256) {for (k.inner: int32, 0, 4) {for (x.inner: int32, 0, 32) {C_2[ramp((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)), 1, 32)] = ((float32x32*)C_2[ramp((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)), 1, 32)] + (broadcast((float32*)A_2[((((x.outer*32768) + (x.inner*1024)) + (k.outer*4)) + k.inner)], 32)*(float32x32*)B_2[ramp((((k.outer*4096) + (k.inner*1024)) + (y.outer*32)), 1, 32)]))}}}}}
}

优化3：Loop Permutation循环置换

如果我们看一下上面的 IR，我们可以看到内环行数据被矢量化，B 被转换成 PackedB（这在内环的（float32x32）B2部分中很明显）。PackedB 的遍历现在是顺序的。因此，我们将研究 A 的访问模式。在当前 schdule中，A 是逐列访问的，这对缓存不友好。如果我们改变嵌套循环顺序 ki 和内部轴 xi，对 A 的访问模式将变得更加缓存友好。

s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)# re-ordering
s[C].reorder(xo, yo, ko, xi, ki, yi)
s[C].vectorize(yi)evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="loop permutation", log=log
)# 再一次打印新生成的 IR
print(tvm.lower(s, [A, B, C], simple_mode=True))

此处输出：

loop permutation: 0.113750
primfn(A_1: handle, B_1: handle, C_1: handle) -> ()attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}buffers = {C: Buffer(C_2: Pointer(float32), float32, [1024, 1024], []),A: Buffer(A_2: Pointer(float32), float32, [1024, 1024], []),B: Buffer(B_2: Pointer(float32), float32, [1024, 1024], [])}buffer_map = {A_1: A, B_1: B, C_1: C} {for (x.outer: int32, 0, 32) {for (y.outer: int32, 0, 32) {for (x.inner.init: int32, 0, 32) {C_2[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = broadcast(0f32, 32)}for (k.outer: int32, 0, 256) {for (x.inner: int32, 0, 32) {for (k.inner: int32, 0, 4) {C_2[ramp((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)), 1, 32)] = ((float32x32*)C_2[ramp((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)), 1, 32)] + (broadcast((float32*)A_2[((((x.outer*32768) + (x.inner*1024)) + (k.outer*4)) + k.inner)], 32)*(float32x32*)B_2[ramp((((k.outer*4096) + (k.inner*1024)) + (y.outer*32)), 1, 32)]))}}}}}
}

优化4：Array Packing数组打包

另一个重要技巧是数组打包。此技巧是对阵列的存储维度重新排序，以便在展平后将特定维度上的连续访问模式转换为序列模式。

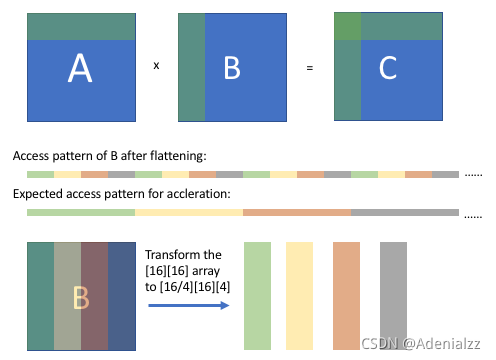
在这里插入图片描述

如上图所示，在阻塞计算后，我们可以观察到 B 的阵列访问模式（平坦后），它是规则的但不连续的。我们希望经过一些转换后，我们可以得到一个连续的访问模式。通过将[16][16]数组重新排序为[16/4][16][4]数组，在从压缩数组中获取相应值时，B 的访问模式将是顺序的。

为了实现这一点，我们必须从一个新的默认 schedule 开始，考虑到 B 的新 wrapper。花点时间对此进行讨论是值得的：TE 是一种用于编写优化算子的功能强大的表达性语言，但它通常需要一些底层算法、数据结构，以及您正在编写的硬件 target。在本教程的后面，我们将讨论让 TVM 承担这一负担的一些选择。不管怎样，让我们继续新的优化 schedule。

# 我们要轻微地重写算法
packedB = te.compute((N / bn, K, bn), lambda x, y, z: B[y, x * bn + z], name="packedB")
C = te.compute((M, N),lambda x, y: te.sum(A[x, k] * packedB[y // bn, k, tvm.tir.indexmod(y, bn)], axis=k),name="C",
)s = te.create_schedule(C.op)xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)s[C].reorder(xo, yo, ko, xi, ki, yi)
s[C].vectorize(yi)x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="array packing", log=log)# 这里是数组打包之后生成的 IR
print(tvm.lower(s, [A, B, C], simple_mode=True))

此处输出：

array packing: 0.224114
primfn(A_1: handle, B_1: handle, C_1: handle) -> ()attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}buffers = {C: Buffer(C_2: Pointer(float32), float32, [1024, 1024], []),A: Buffer(A_2: Pointer(float32), float32, [1024, 1024], []),B: Buffer(B_2: Pointer(float32), float32, [1024, 1024], [])}buffer_map = {A_1: A, B_1: B, C_1: C} {allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global {for (x: int32, 0, 32) "parallel" {for (y: int32, 0, 1024) {packedB[ramp(((x*32768) + (y*32)), 1, 32)] = (float32x32*)B_2[ramp(((y*1024) + (x*32)), 1, 32)]}}for (x.outer: int32, 0, 32) {for (y.outer: int32, 0, 32) {for (x.inner.init: int32, 0, 32) {C_2[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = broadcast(0f32, 32)}for (k.outer: int32, 0, 256) {for (x.inner: int32, 0, 32) {for (k.inner: int32, 0, 4) {C_2[ramp((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)), 1, 32)] = ((float32x32*)C_2[ramp((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)), 1, 32)] + (broadcast((float32*)A_2[((((x.outer*32768) + (x.inner*1024)) + (k.outer*4)) + k.inner)], 32)*(float32x32*)packedB[ramp((((y.outer*32768) + (k.outer*128)) + (k.inner*32)), 1, 32)]))}}}}}}
}

优化5：Optimizing Block Writing Through Caching通过缓存优化块写入

到目前为止，我们所有的优化都集中在高效地访问和计算来自 A 和 B 矩阵的数据，以计算C矩阵。阻塞优化后，操作员将结果逐块写入 C，并且访问模式不是顺序的。我们可以通过使用顺序缓存数组来解决这个问题，使用cache_write、compute_at 和 unroll 的组合来保存块结果，并在所有块结果就绪时写入到 C。

s = te.create_schedule(C.op)# Allocate write cache
CC = s.cache_write(C, "global")xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)# Write cache is computed at yo
s[CC].compute_at(s[C], yo)# New inner axes
xc, yc = s[CC].op.axis(k,) = s[CC].op.reduce_axis
ko, ki = s[CC].split(k, factor=4)
s[CC].reorder(ko, xc, ki, yc)
s[CC].unroll(ki)
s[CC].vectorize(yc)x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="block caching", log=log)# Here is the generated IR after write cache blocking.
print(tvm.lower(s, [A, B, C], simple_mode=True))

此处输出：

block caching: 0.224213
primfn(A_1: handle, B_1: handle, C_1: handle) -> ()attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}buffers = {C: Buffer(C_2: Pointer(float32), float32, [1024, 1024], []),A: Buffer(A_2: Pointer(float32), float32, [1024, 1024], []),B: Buffer(B_2: Pointer(float32), float32, [1024, 1024], [])}buffer_map = {A_1: A, B_1: B, C_1: C} {allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global;allocate(C.global: Pointer(global float32), float32, [1024]), storage_scope = global {for (x: int32, 0, 32) "parallel" {for (y: int32, 0, 1024) {packedB[ramp(((x*32768) + (y*32)), 1, 32)] = (float32x32*)B_2[ramp(((y*1024) + (x*32)), 1, 32)]}}for (x.outer: int32, 0, 32) {for (y.outer: int32, 0, 32) {for (x.c.init: int32, 0, 32) {C.global[ramp((x.c.init*32), 1, 32)] = broadcast(0f32, 32)}for (k.outer: int32, 0, 256) {for (x.c: int32, 0, 32) {C.global[ramp((x.c*32), 1, 32)] = ((float32x32*)C.global[ramp((x.c*32), 1, 32)] + (broadcast((float32*)A_2[(((x.outer*32768) + (x.c*1024)) + (k.outer*4))], 32)*(float32x32*)packedB[ramp(((y.outer*32768) + (k.outer*128)), 1, 32)]))C.global[ramp((x.c*32), 1, 32)] = ((float32x32*)C.global[ramp((x.c*32), 1, 32)] + (broadcast((float32*)A_2[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 1)], 32)*(float32x32*)packedB[ramp((((y.outer*32768) + (k.outer*128)) + 32), 1, 32)]))C.global[ramp((x.c*32), 1, 32)] = ((float32x32*)C.global[ramp((x.c*32), 1, 32)] + (broadcast((float32*)A_2[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 2)], 32)*(float32x32*)packedB[ramp((((y.outer*32768) + (k.outer*128)) + 64), 1, 32)]))C.global[ramp((x.c*32), 1, 32)] = ((float32x32*)C.global[ramp((x.c*32), 1, 32)] + (broadcast((float32*)A_2[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 3)], 32)*(float32x32*)packedB[ramp((((y.outer*32768) + (k.outer*128)) + 96), 1, 32)]))}}for (x.inner: int32, 0, 32) {for (y.inner: int32, 0, 32) {C_2[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] = (float32*)C.global[((x.inner*32) + y.inner)]}}}}}
}

优化6：Parallelization并行化

# 并行
s[C].parallel(xo)x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="parallelization", log=log
)# 这里是并行化之后的 IR
print(tvm.lower(s, [A, B, C], simple_mode=True))

此处输出：

parallelization: 0.067949
primfn(A_1: handle, B_1: handle, C_1: handle) -> ()attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}buffers = {C: Buffer(C_2: Pointer(float32), float32, [1024, 1024], []),A: Buffer(A_2: Pointer(float32), float32, [1024, 1024], []),B: Buffer(B_2: Pointer(float32), float32, [1024, 1024], [])}buffer_map = {A_1: A, B_1: B, C_1: C} {allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global {for (x: int32, 0, 32) "parallel" {for (y: int32, 0, 1024) {packedB[ramp(((x*32768) + (y*32)), 1, 32)] = (float32x32*)B_2[ramp(((y*1024) + (x*32)), 1, 32)]}}for (x.outer: int32, 0, 32) "parallel" {allocate(C.global: Pointer(global float32), float32, [1024]), storage_scope = global;for (y.outer: int32, 0, 32) {for (x.c.init: int32, 0, 32) {C.global[ramp((x.c.init*32), 1, 32)] = broadcast(0f32, 32)}for (k.outer: int32, 0, 256) {for (x.c: int32, 0, 32) {C.global[ramp((x.c*32), 1, 32)] = ((float32x32*)C.global[ramp((x.c*32), 1, 32)] + (broadcast((float32*)A_2[(((x.outer*32768) + (x.c*1024)) + (k.outer*4))], 32)*(float32x32*)packedB[ramp(((y.outer*32768) + (k.outer*128)), 1, 32)]))C.global[ramp((x.c*32), 1, 32)] = ((float32x32*)C.global[ramp((x.c*32), 1, 32)] + (broadcast((float32*)A_2[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 1)], 32)*(float32x32*)packedB[ramp((((y.outer*32768) + (k.outer*128)) + 32), 1, 32)]))C.global[ramp((x.c*32), 1, 32)] = ((float32x32*)C.global[ramp((x.c*32), 1, 32)] + (broadcast((float32*)A_2[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 2)], 32)*(float32x32*)packedB[ramp((((y.outer*32768) + (k.outer*128)) + 64), 1, 32)]))C.global[ramp((x.c*32), 1, 32)] = ((float32x32*)C.global[ramp((x.c*32), 1, 32)] + (broadcast((float32*)A_2[((((x.outer*32768) + (x.c*1024)) + (k.outer*4)) + 3)], 32)*(float32x32*)packedB[ramp((((y.outer*32768) + (k.outer*128)) + 96), 1, 32)]))}}for (x.inner: int32, 0, 32) {for (y.inner: int32, 0, 32) {C_2[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] = (float32*)C.global[((x.inner*32) + y.inner)]}}}}}
}

矩阵乘例子的总结

在仅用 18 行代码应用上述简单优化之后，我们生成的代码就可以得到与使用数学内核库（MKL）的 numpy 接近的性能。我们刚才一直都记录了性能，因此在这里可以直接比较结果：

baseline = log[0][1]
print("%s\t%s\t%s" % ("Operator".rjust(20), "Timing".rjust(20), "Performance".rjust(20)))
for result in log:print("%s\t%s\t%s"% (result[0].rjust(20), str(result[1]).rjust(20), str(result[1] / baseline).rjust(20)))

此处输出：

        Operator                  Timing             Performancenone            3.1094061458                     1.0blocking     0.29192816779999997     0.09388550549895809vectorization            0.3312631714     0.10653583220302389
loop permutation            0.1137497149    0.036582456445468314array packing            0.2241142794     0.07207623221003798block caching     0.22421289339999997     0.07210794694763607parallelization            0.0679485881    0.021852593361526892

请注意，以上的输出反映的是非独占 Docker 容器上的运行时间，因此并不可靠。强烈建议您自己运行本教程，观察 TVM 实现的性能增益，并仔细阅读每个示例，以了解矩阵乘法运算的迭代改进。