在生活中我们经常会用到决策树算法,最简单的就是二叉树了;相信大家也会又同样的困扰,手机经常收到各种短信,其中不乏很多垃圾短信、此时只要设置这类短信为垃圾短信手机就会自动进行屏蔽、减少被骚扰的次数,同时正常短信又不会被阻拦。类似这种就是决策树的工作原理,决策树的一个重要任务是为了理解数据中所含的信息,可以使用决策树不熟悉的数据集合,并从中体取一系列规则,这些机器根据数据集创建规则的过程,就是机器学习的过程。
决策树优缺点:
优点:计算复杂度不高,输出结果易于理解、即对模型的输出结果的可解释性要高;对中间值的缺失不敏感,可以处理不相关数据;
缺点:可能会产生过拟合现象;
决策树的构建:
输入:数据集
输出:构建好的决策树(训练集)
def 创建决策树:
if(数据集中所有样本分类一致):
创建携带类标签的叶子节点
else:
寻找划分数据集最好的特征
根据最好特征划分数据集
for每个划分的数据集:
创建决策子树(递归完成)
决策树的关键在于当前数据集上选择哪个特征属性作为划分的条件(能够将本来无序的数据集最大程度的划分为有序的子集),度量最佳分类属性特征的“最佳性”可用非纯度进行衡量;如果一个数据集只有一种分类结果,则该数据集一致性好、能够提供的信息也最少:只有一种情况;如果数据集有很多分类,则该数据集的一致性不好,能够提供的信息也较多:至少确定不只一种。组织杂乱数据的一种方法就是使用信息论度量信息,在划分数据前后信息发生的变化称为信息增益、这里描述集合信息的度量方式称为香农熵或者简称熵。(该名字来源于克劳德.香农、二十实际最聪明的人之一)。熵定义为信息的期望值,为了计算熵、我们需要计算所有类别的可能值所包含的信息期望。
熵计算公式:
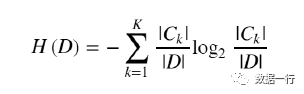
明确决策树分类选择特征的依据后,先梳理下决策树的流程都有哪些:
1、收集数据:一切可以使用的方法、只要不违法;
2、准备数据:树构造算法只适用于标准型数据,因此数据值必须离散化;
3、分析数据:可以使用任何方法,数据构建完成后,需看下是否达到了我们的预期;
4、训练算法:构建树的数据结构;
5、测试算法:使用构建好的树计算正确率,越高当然越好(也可能过拟合、不能过份高了);
6、使用算法。
为了后面更好的理解决策树,利用如下数据我们先套用下公式,直观的计算一下什么是信息熵、什么是信息增益,以及如何选择一个特征作为当前数据的划分条件;以便后面更好的撸代码。
经典的样例数据:
Day | 天气 | 温度 | 湿度 | 风 | 决定 |
1 | 晴 | 热 | 高 | 弱 | N |
2 | 晴 | 热 | 高 | 强 | N |
3 | 阴 | 热 | 高 | 弱 | Y |
4 | 雨 | 中 | 高 | 弱 | Y |
5 | 雨 | 凉 | 正常 | 弱 | Y |
6 | 雨 | 凉 | 正常 | 强 | N |
7 | 阴 | 凉 | 正常 | 强 | Y |
8 | 晴 | 中 | 高 | 弱 | N |
9 | 晴 | 凉 | 正常 | 弱 | Y |
10 | 雨 | 中 | 正常 | 弱 | Y |
11 | 晴 | 中 | 正常 | 强 | Y |
12 | 阴 | 中 | 高 | 强 | Y |
13 | 阴 | 热 | 正常 | 弱 | Y |
14 | 雨 | 中 | 高 | 强 | N |
根据信息熵的公式,此数据比较简单、我们可以手工计算一下各个特征的信息增益,从而知道ID3算法具体选择哪个特征作为分类的依据和算法的一个计算过程。
先列一下公式、参照公式带入计算,减小手工计算误差:
计算数据集(D)的经验熵:
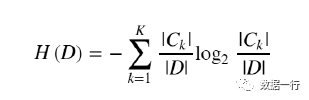
一个特征(A)对数据集(D)的经验条件熵:
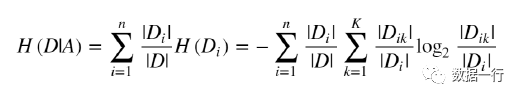
那么相对特征(A)此时的信息增益计算公式为:
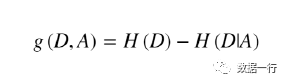
以上4个特征中:天气(晴、阴雨)/温度(热、适中、凉)/湿度(高、正常)/风(强弱),推算过程中我们选择湿度或风、这两个特征值分布均只含两个值,计算过程的时候相对要简单一点。
第一步:计算该数据集的经验熵,该数据集共有14条数据:9条决定为Y、5条决定为N;则p(Y)=9/14、p(N)=5/14。此时代入公式:
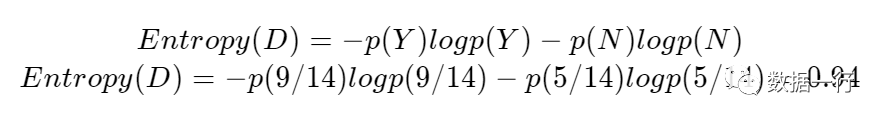
第二步:选择风这个特征计算该特征相对数据集的经验熵,从数据可以看出风共有两个值:强和弱。
其中为强风的数据分布如下、共有6条数据,其中决定为Y和N的分别是3条,此时p(Y)=3/6、p(N)=3/6。
Day | 天气 | 温度 | 湿度 | 风 | 决定 |
2 | 晴 | 热 | 高 | 强 | N |
6 | 雨 | 凉 | 正常 | 强 | N |
7 | 阴 | 凉 | 正常 | 强 | Y |
11 | 晴 | 中 | 正常 | 强 | Y |
12 | 阴 | 中 | 高 | 强 | Y |
14 | 雨 | 中 | 高 | 强 | N |
代入公式:
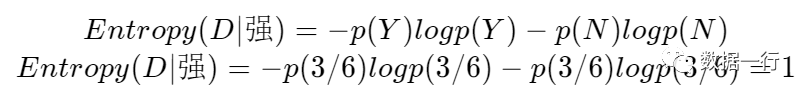
其中为若风的数据分布如下、共有8条数据,其中决定为Y有6条、N有2条,此时p(Y)=6/8、p(N)=2/8。
Day | 天气 | 温度 | 湿度 | 风 | 决定 |
1 | 晴 | 热 | 高 | 弱 | N |
3 | 阴 | 热 | 高 | 弱 | Y |
4 | 雨 | 中 | 高 | 弱 | Y |
5 | 雨 | 凉 | 正常 | 弱 | Y |
8 | 晴 | 中 | 高 | 弱 | N |
9 | 晴 | 凉 | 正常 | 弱 | Y |
10 | 雨 | 中 | 正常 | 弱 | Y |
13 | 阴 | 热 | 正常 | 弱 | Y |
代入公式:
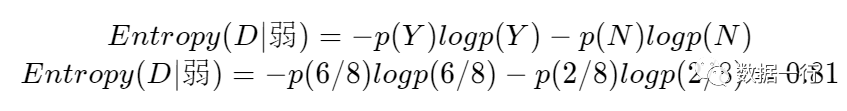
风这个特征的经验熵计算就完成了,强风和弱风在整个数据集中的占比分别为:
p(强)=6/14、p(弱)=8/14;代入公式则风这个特征的条件熵为:
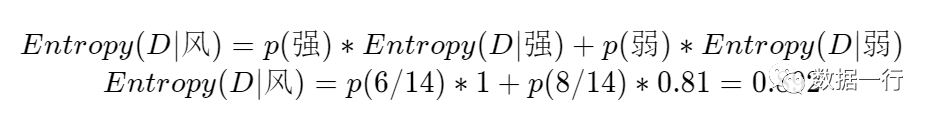
风这个特征的信息增益为:
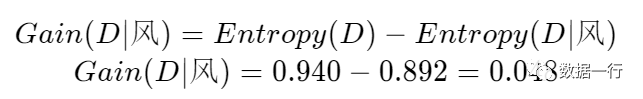
以此类推:

从中可以看出天气的新增增益为0.246、高于其他三个特征的增益,这也是为什么天气作为第一个分类依据的特征、在树的根节点上。
参照《机器学习实践》构建一颗决策树、python代码如下:
from math import logimport operatordef calcShannonEnt(dataSet): # 计算数据的熵(entropy) numEntries = len(dataSet) # 数据条数 labelCounts = {} for featVec in dataSet: currentLabel = featVec[-1] # 每行数据的最后一个字(类别) if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 # 统计有多少个类以及每个类的数量 shannonEnt = 0 for key in labelCounts: prob = float(labelCounts[key]) / numEntries # 计算单个类的熵值 shannonEnt -= prob * log(prob, 2) # 累加每个类的熵值 return shannonEntdef createDataSet1(): # 创造示例数据 dataSet = [['黑', '是', '男'], ['白', '否', '男'], ['黑', '是', '男'], ['白', '否', '女'], ['黑', '是', '女'], ['黑', '否', '女'], ['白', '否', '女'], ['白', '否', '女']] labels = ['a', 'b'] return dataSet, labels#待划分的数据集、划分数据集的特征、需要返回的特征值def splitDataSet(dataSet, axis,value): # 按某个特征分类后的数据,例如value = 长,axis为头发axis = 0 retDataSet = [] # retDataSet返回的是数据中,所有头发为长的记录 for featVec in dataSet: if featVec[axis] == value: # 每次会将这个feature删除掉 reducedFeatVec = featVec[:axis] reducedFeatVec.extend(featVec[axis + 1:]) retDataSet.append(reducedFeatVec) return retDataSetdef chooseBestFeatureToSplit(dataSet): # 选择最优的分类特征 numFeatures = len(dataSet[0]) - 1 baseEntropy = calcShannonEnt(dataSet) # 原始的熵 bestInfoGain = 0 bestFeature = -1 # (1)遍历每个特征 for i in range(numFeatures): featList = [example[i] for example in dataSet] uniqueVals = set(featList) newEntropy = 0 # (2)对单个特征中每个唯一值都进行子树的切分,然后计算这个的信息增益,然后累加每个分裂条件的信息增益,为newEntropy for value in uniqueVals: subDataSet = splitDataSet(dataSet, i, value) prob = len(subDataSet) / float(len(dataSet)) newEntropy += prob * calcShannonEnt(subDataSet) # 按特征分类后的熵 infoGain = baseEntropy - newEntropy # 原始熵与按特征分类后的熵的差值 if (infoGain > bestInfoGain): # 若按某特征划分后,熵值减少的最大,则次特征为最优分类特征 bestInfoGain = infoGain bestFeature = i return bestFeaturedef majorityCnt(classList): #按分类后类别数量排序,比如:最后分类为2男1女,则判定为男; classCount = {} for vote in classList: if vote not in classCount.keys(): classCount[vote] = 0 classCount[vote] += 1 sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0]# 决策树核心逻辑:递归,深度优先遍历创建子树def createTree(dataSet, labels): #print(dataSet) classList = [example[-1] for example in dataSet] # 类别:男或女 if classList.count(classList[0]) == len(classList): return classList[0] if len(dataSet[0]) == 1: # 当只剩最优一个feature时,因为每次分裂会删除一个特征 return majorityCnt(classList) # (1) 选择最优分裂特征 bestFeat = chooseBestFeatureToSplit(dataSet) #选择最优特征 bestFeatLabel = labels[bestFeat] myTree = {bestFeatLabel: {}} #分类结果以字典形式保存 del (labels[bestFeat]) featValues = [example[bestFeat] for example in dataSet] uniqueVals = set(featValues) # (2) 遍历分裂特征的每个唯一值,分裂产生子树 for value in uniqueVals: # 将每个label都往子树传递,labels一直可能会被选用 subLabels = labels[:] # 对基于best feature这个feature内每个唯一值切分为不同的子树,然后返回子树的结果。每个子树切分能多个分支 # 递归调用,每层的切分为每个特征的唯一值 # (3) 对最佳分裂特征的每个值,分别创建子树 myTree[bestFeatLabel][value] = createTree( splitDataSet(dataSet, bestFeat, value), subLabels) return myTreeif __name__ == '__main__': dataSet, labels = createDataSet1() # 创造示列数据 print(createTree(dataSet, labels)) # 输出决策树模型结果from sklearn.datasets import load_irisfrom sklearn import treeimport osimport pydot # need installprint(os.getcwd())clf = tree.DecisionTreeClassifier(criterion="entropy", max_features="log2",max_depth = 10) #giniiris = load_iris()clf = clf.fit(iris.data, iris.target)tree.export_graphviz(clf, out_file='tree.dot')(graph, ) = pydot.graph_from_dot_file('tree.dot')graph.write_png('tree.png')对应的决策树结构如下:
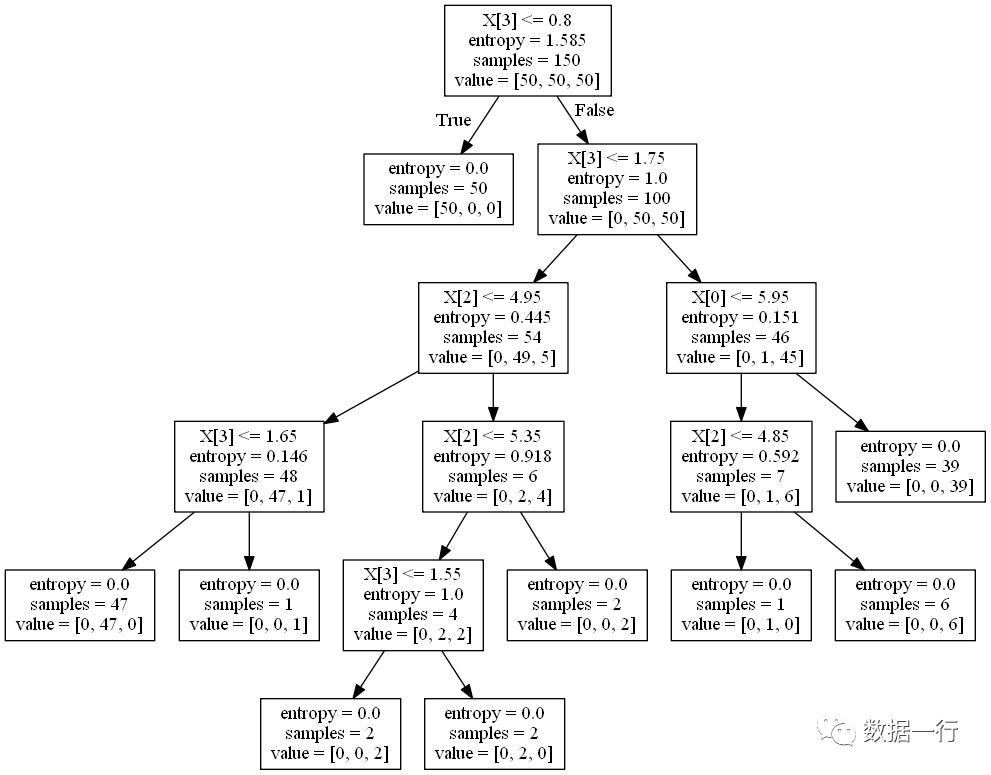
ID3是基于信息增益作为分类依据的监督学习算法,它有一个明显的缺点是该算法会倾向选择有较多属性值的特征作为分类依据,鉴于ID3算法缺点后面又衍生出来C4.5和CART算法、具体后面再详细介绍和分享总结。



















