问题定义：

巡回旅行商问题

给定一组n个城市和俩俩之间的直达距离，寻找一条闭合的旅程，使得每个城市刚好经过一次且总的旅行距离最短。

TSP问题也称为货郎担问题，是一个古老的问题。最早可以追溯到1759年Euler提出的骑士旅行的问题。1948年，由美国兰德公司推动，TSP成为近代组合优化领域的典型难题。

TSP是一个具有广泛的应用背景和重要理论价值的组合优化问题。近年来，有很多解决该问题的较为有效的算法不断被推出，例如Hopfield神经网络方法，模拟退火方法以及遗传算法方法等。

TSP搜索空间随着城市数n的增加而增大,所有的旅程路线组合数为(n-1)!/2。在如此庞大的搜索空间中寻求最优解，对于常规方法和现有的计算工具而言，存在着诸多计算困难。借助遗传算法的搜索能力解决TSP问题，是很自然的想法。

基本遗传算法可定义为一个8元组：

• (SGA)=(C，E，P0，M，Φ，Г，Ψ，Τ)

• C ——个体的编码方法，SGA使用固定长度二进制符号串编码方法；

• E ——个体的适应度评价函数；

• P0——初始群体；

• M ——群体大小，一般取20—100；

• Ф——选择算子，SGA使用比例算子；

• Г——交叉算子，SGA使用单点交叉算子；

• Ψ——变异算子，SGA使用基本位变异算子；

• Т——算法终止条件，一般终止进化代数为100—500；

问题的表示

• 对于一个实际的待优化问题，首先需要将其表示为适合于遗传算法操作的形式。用遗传算法解决TSP，一个旅程很自然的表示为n个城市的排列，但基于二进制编码的交叉和变异操作不能适用。

• 路径表示是表示旅程对应的基因编码的最自然，最简单的表示方法。它在编码，解码，存储过程中相对容易理解和实现。例如：旅程(5-1-7-8-9-4-6-2-3)可以直接表示为(5 1 7 8 9 4 6 2 3)。

产生初始种群

• 一是完全随机产生，它适合于对问题的解无任何先验知识的情况。随机性较强，因而也较公正。

• 二是某些先验知识可转变为必须满足的一组要求，然后在满足这些要求的解中在随机地选取样本。这样选择初始种群可使遗传算法更快的达到最优解。种群有一定的目标性和代表性，但取例不如完全随机的广泛，而且先验知识是否可靠也是一个问题。

适应度函数

• 遗传算法在进化搜索中基本不利用外部信息,仅以适应度函数为依据,利用种群中每个个体的适应度值来进行搜索。TSP的目标是路径总长度为最短，路径总长度的倒数就可以为TSP的适应度函数：

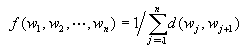
选择

一般地说，选择将使适应度较大(优良)个体有较大的存在机会，而适应度较小(低劣)的个体继续存在的机会也较小。简单遗传算法采用赌轮选择机制，令Σfi表示群体的适应度值之总和，fi表示种群中第i个染色体的适应度值，它产生后代的能力正好为其适应度值所占份额fi／Σfi。

交叉

基于路径表示的编码方法，要求一个个体的染色体编码中不允许有重复的基因码，也就是说要满足任意一个城市必须而且只能访问一次的约束。基本遗传算法的交叉操作生成的个体一般不能满足这一约束条件。

部分匹配交叉操作要求随机选取两个交叉点，以便确定一个匹配段，根据两个父个体中两个交叉点之间的中间段给出的映射关系生成两个子个体。

变异

遗传算法解决TSP 问题基于二进值编码的变异操作不能适用，不能够由简单的变量的翻转来实现

在TSP问题中个体的编码是一批城市的序列，随机的在这个序列抽取两个城市，然后交换他们的位置。这样就实现了个体编码的变异，算法如下：

1. 产生两个0到1之间的随机实数；

2. 将这两个随机实数转化为0到n(城市数)-1之间的随机整数；

3. 将这两个随机整数指代的城市进行交换；

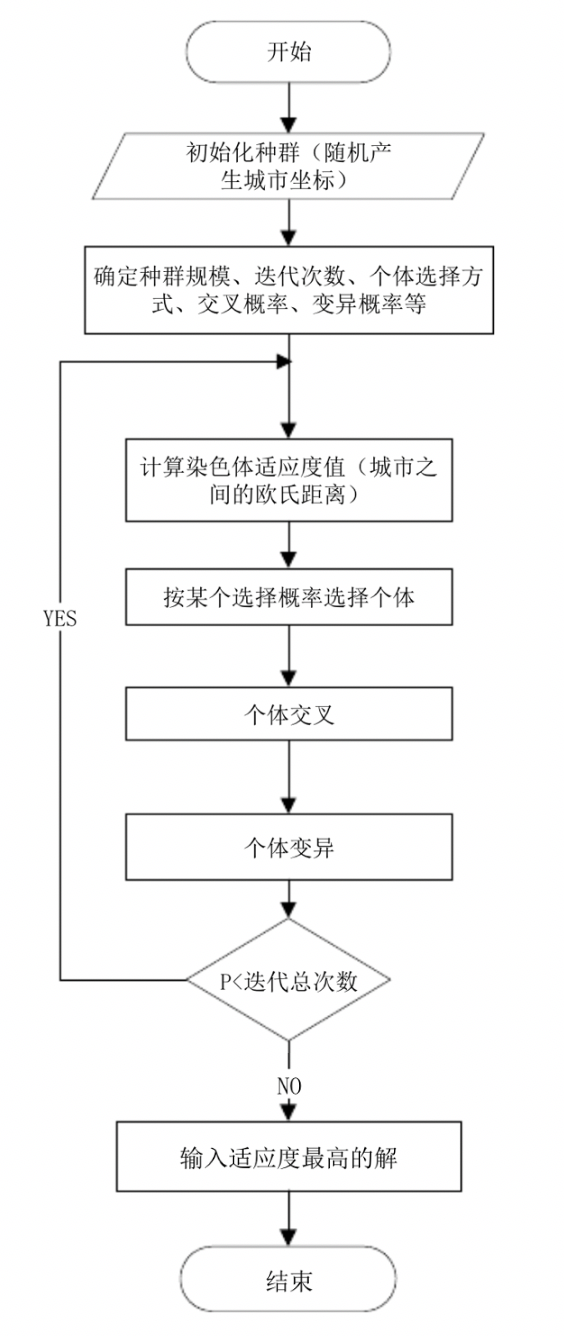
流程图

代码

主函数代码：

clear;

clc;

tStart= tic;% 算法计时器

%%%%%%%%%%%%自定义参数%%%%%%%%%%%%%

[cityNum,cities]= Read('dsj1000.tsp');

cities= cities';

%cityNum=100;

maxGEN = 1000;

popSize = 100; % 遗传算法种群大小

crossoverProbabilty = 0.9; %交叉概率

mutationProbabilty = 0.1; %变异概率

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

gbest = Inf;

%随机生成城市位置

%cities=rand(2,cityNum)*100;%100是最远距离

%计算上述生成的城市距离

distances = calculateDistance(cities);

%生成种群，每个个体代表一个路径

pop = zeros(popSize, cityNum);

for i=1:popSize

    pop(i,:) = randperm(cityNum);

end

offspring = zeros(popSize,cityNum);

%保存每代的最小路劲便于画图

minPathes = zeros(maxGEN,1);

%GA算法

for  gen=1:maxGEN

    % 计算适应度的值，即路径总距离

    [fval, sumDistance, minPath, maxPath] = fitness(distances, pop);

    % 轮盘赌选择

    tournamentSize=4; %设置大小

    for k=1:popSize

        % 选择父代进行交叉

        tourPopDistances=zeros( tournamentSize,1);

        for i=1:tournamentSize

            randomRow = randi(popSize);

            tourPopDistances(i,1) = sumDistance(randomRow,1);

        end

        % 选择最好的，即距离最小的

        parent1  = min(tourPopDistances);

        [parent1X,parent1Y] = find(sumDistance==parent1,1, 'first');

        parent1Path = pop(parent1X(1,1),:);

        for i=1:tournamentSize

            randomRow = randi(popSize);

            tourPopDistances(i,1) = sumDistance(randomRow,1);

        end

        parent2  = min(tourPopDistances);

        [parent2X,parent2Y] = find(sumDistance==parent2,1, 'first');

        parent2Path = pop(parent2X(1,1),:);

        subPath = crossover(parent1Path, parent2Path, crossoverProbabilty);%交叉

        subPath = mutate(subPath, mutationProbabilty);%变异

        offspring(k,:) = subPath(1,:);

        minPathes(gen,1) = minPath;

    end

    fprintf('代数:%d   最短路径:%.2fKM \n', gen,minPath);

    % 更新

    pop= offspring;

    % 画出当前状态下的最短路径

    ifminPath< gbest

        gbest= minPath;

        paint(cities,pop,gbest,sumDistance,gen);

    end

end

figure

plot(minPathes,'MarkerFaceColor','red','LineWidth',1);

title('收敛曲线图(每一代的最短路径)');

set(gca,'ytick',500:100:5000);

ylabel('路径长度');

xlabel('迭代次数');

gridon

tEnd= toc(tStart);

fprintf('时间:%d 分  %f 秒.\n',floor(tEnd/60),rem(tEnd,60));

function[distances]= calculateDistance(city)

%计算距离

    [~,col]= size(city);

    distances= zeros(col);

    fori=1:col

        forj=1:col

            distances(i,j)= distances(i,j)+ sqrt((city(1,i)-city(1,j))^2+ (city(2,i)-city(2,j))^2  );          

        end

    end

end

function[childPath]= crossover(parent1Path,parent2Path,prob)

%交叉

    random= rand();

    ifprob>= random

        [l,length]= size(parent1Path);

        childPath= zeros(l,length);

        setSize= floor(length/2)-1;

        offset= randi(setSize);

        fori=offset:setSize+offset-1

            childPath(1,i)= parent1Path(1,i);

        end

        iterator= i+1;

        j= iterator;

        whileany(childPath== 0)

            ifj> length

                j= 1;

            end

            ifiterator> length

                iterator= 1;

            end

            if~any(childPath== parent2Path(1,j))

                childPath(1,iterator)= parent2Path(1,j);

               iterator= iterator+ 1;

            end

            j= j+ 1;

        end

    else

        childPath= parent1Path;

    end

end

function[fitnessvar,sumDistances,minPath,maxPath]= fitness(distances,pop)

%计算整个种群的适应度值

    [popSize,col]= size(pop);

    sumDistances= zeros(popSize,1);

    fitnessvar= zeros(popSize,1);

    fori=1:popSize

       forj=1:col-1

          sumDistances(i)= sumDistances(i)+ distances(pop(i,j),pop(i,j+1));

       end

    end

    minPath= min(sumDistances);

    maxPath= max(sumDistances);

    fori=1:length(sumDistances)

        fitnessvar(i,1)=(maxPath- sumDistances(i,1)+0.000001)/ (maxPath-minPath+0.00000001);

    end

end

function[mutatedPath]= mutate(path,prob)

%对指定的路径利用指定的概率进行更新

    random= rand();

    ifrandom<= prob

        [l,length]= size(path);

        index1= randi(length);

        index2= randi(length);

        %交换

        temp= path(l,index1);

        path(l,index1)= path(l,index2);

        path(l,index2)=temp;

    end

        mutatedPath= path;

end

function[output_args]= paint(cities,pop,minPath, totalDistances, gen)

    gNumber=gen;

    [~,length]= size(cities);

    xDots= cities(1,:);

    yDots= cities(2,:);

    %figure(1);

    title('GA TSP');

    plot(xDots,yDots,'p','MarkerSize',14,'MarkerFaceColor','blue');

    xlabel('经度');

    ylabel('纬度');

    axisequal

    holdon

    [minPathX,~]= find(totalDistances==minPath,1,'first');

    bestPopPath= pop(minPathX,:);

    bestX= zeros(1,length);

    bestY= zeros(1,length);

    forj=1:length

       bestX(1,j)= cities(1,bestPopPath(1,j));

       bestY(1,j)= cities(2,bestPopPath(1,j));

    end

    title('GA TSP');

    plot(bestX(1,:),bestY(1,:),'red','LineWidth',1.25);

    legend('城市','路径');

    axisequal

    gridon

    %text(5,0,sprintf('迭代次数: %d 总路径长度: %.2f',gNumber, minPath),'FontSize',10);

    drawnow

    holdoff

end

function[n_citys,city_position]= Read(filename)

fid= fopen(filename,'rt');

location=[];

A= [12];

tline= fgetl(fid);

whileischar(tline)

    if(strcmp(tline,'NODE_COORD_SECTION'))

        while~isempty(A)

            A=fscanf(fid,'%f',[3,1]);

            ifisempty(A)

                break;

            end

            location=[location;A(2:3)'];

        end

    end

    tline = fgetl(fid);

    if strcmp(tline,'EOF')

        break;

    end

end

[m,n]=size(location);

n_citys= m;

city_position=location;

fclose(fid);

end

结果

测试数据：

初始态：

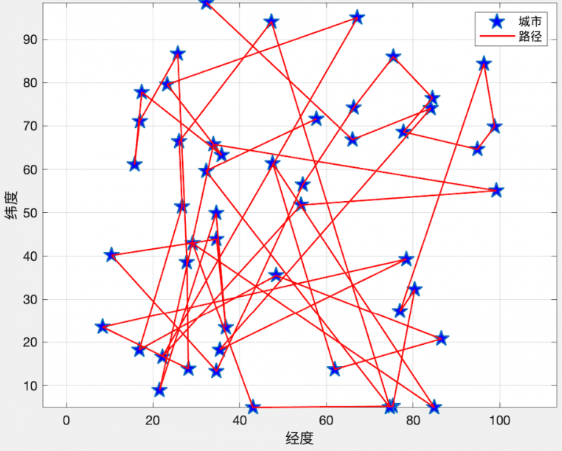
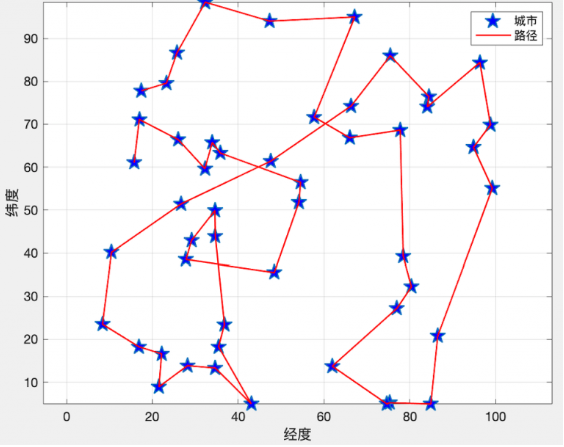
终态：

收敛曲线：

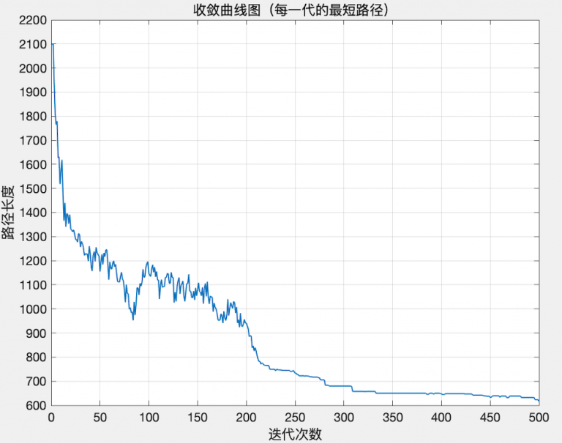
可以看到，当城市数量适中时，迭代500次最短路径长度有收敛的趋势。

当城市数目较多时

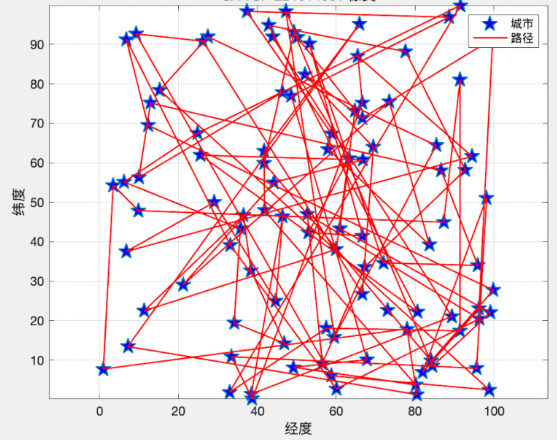
迭代500次，仍然不收敛，可能的问题是陷入了局部最优解。

总结与观点

难点是交叉算法的设计，由于TSP问题和一般的NP问题不一样，每个个体的每个维度具有唯一性，因此在交叉的时候要注意不能有重复的值。本次实验采用的是部分匹配交叉，先从第一个父代选出一个偏移量，从偏移量后的部分点加入到子代，接下来从第二个父代选择第一代没有选择的部分点移到子代中。

当城市数量较多时，大于50个城市，迭代多次，GA仍然不收敛，可能的问题是陷入了局部最优解，因此对GA算法进行改进怡跳出局部最优解，可以采用类似于PSO或者蚁群算法的思想。

数据集下载

https://github.com/xyjigsaw/Dataset

转载自：

https://www.omegaxyz.com/2019/01/21/matlab-tsp-all/

作者：OmegaXYZ

https://www.omegaxyz.com