特征选择就是从原始特征中选取一些最有效的特征来降低维度,,提高模型泛化能力减低过拟合的过程,主要目的是剔除掉无关特征和冗余特征,选出最优特征子集;
常见的特征选择方法可以分为3类:过滤式(filter)、包裹式(wrapper)、嵌入式(embedding)。
1.过滤式filter:
通过方差选择法、相关系数法、卡方检验法、互信息法来对特征进行评分,设定阈值或者待选择的阈值的个数来选择;
1.1方差选择法
计算各个特征的方差,剔除小于设定的阈值的特征,剔除特征值 波动较小的特征,例如一个特征的所有值都为1,那这个特征对于预测目标变量就没什么作用;方法很简单,但实际应用中只有少数变量才会存在只取某个值的情况,对特征选择作用比较小,可以当做数据预处理部分,之后再用其他方法进行特征选择。
from sklearn.feature_selection import VarianceThreshold
var = VarianceThreshold(threshold=0)
var.fit_transform(df)
df = df.iloc[var.get_support(True),:]
#VarianceThreshold返回已经提出方差为0的列,通过get_support[True]定位
剩余变量所在的列
1.2 单变量特征选择
1.2.1相关系数法
皮尔森相关系数衡量的是变量之间的线性相关性,取值范围在-1-+1之间,-1表示完全负相关,+1表示完全正相关,0表示线性无关;
可以使用scipy的pearsonr 计算皮尔森相关系数,且它还可以同时计算出p值
import numpy as np
from scipy.stats import pearsonr
x = np.random.normal(0,10,300)
y = x + np.random.normal(0,10,300)
pearsonr(x,y)
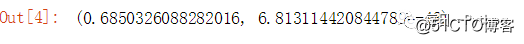
但是皮尔森相关系数只衡量线性关系,即使两个变量之间有较强的非线性关系,皮尔森系数也有可能接近为0;
1.2.2.卡方检验法
检验定性自变量对定性因变量的相关性,卡方公式为:
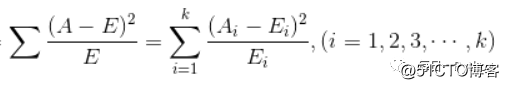
其中Ai为观测频数,Ei为期望频数
from sklearn.feature_selection import chi2
#chi2要求变量值非负,返回卡方值和P值
from sklearn.feature_selection import SelectKBest
from sklearn.datasets import load_iris
iris = load_iris()
model = SelectKBest(chi2, k=2)
model.fit_transform(iris.data,iris.target)
var = model.get_support(True)
1.2.3 互信息法和最大信息系数
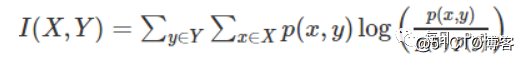
互信息法也是评价定性自变量对定性因变量的相关性的,但是并不方便直接用于特征选择,一是因为它不属于度量方式,也没有办法进行归一化,在不同的数据上的结果无法做比较;二是因为对于连续变量的计算不是很方便,通常需要将变量离散化,而互信息的结果对离散化的方法很敏感;
因此引入了最大信息系数 。最大信息系数首先寻找一种最优的离散方式,然后把互信息取值转换成一种度量方式,取值区间在[0,1],minepy模块提供了MIC(最大信息系数)方法:
x = np.random.normal(0,10,300)
z = x *x
pearsonr(x,z)
#计算得皮尔森系数= -0.1
from minepy import MINE
m = MINE()
m.compute_score(x, z)
print(m.mic())
#mic系数= 1.0
1.2.4 距离相关系数法
距离相关系数是为了克服皮尔森相关系数只能衡量线性关系的弱点而生的。x和x^2的皮尔森相关系数可能接近于0,但是这两个变量并不是独立不相关的。使用距离相关系数就可以计算x和x^2的非线性关系,如果距离相关系数接近于0,就可以说两个变量之间是独立的。R语言的energy包提供了距离相关系数的函数,Python没有直接计算的包,可以查看https://gist.github.com/josef-pkt/2938402;
#R语言
x
z
dcor(x, z)
计算得 x,x**2的距离相关系数为0.98
2.包裹式Wrapper
根据预测效果(AUC/MSE)或者其他方法对特征组合进行评分,主要方法有递归特征消除法;
递归特征消除法的主要思想是反复的构建模型,然后选出最好或最坏的特征,把选出的特征放到一边,然后在剩余的特征上重复这个过程,直到所有特征都遍历了。在这个过程中特征被消除的次序就是特征的排序。
from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
rfe = RFE(lr, n_features_to_select=2)
rfe.fit(iris.data, iris.target)
var = rfe.get_support(True)
3.嵌入式Embedded
3.1正则化
正则化主要包括L1正则化和L2正则化:
L1正则化将系数W的L1范数作为惩罚项加到损失函数中,L1正则方法具有稀疏解的特性,因此天然具有特征选择的特性,但是不代表没被选到的特征就不重要,有可能是因为两个高度相关的特征最后只保留了一个;另外L1正则化和非正则化模型一样是不稳定的,如果特征集合中具有相关联的特征,当数据发生细微变化时也有可能导致很大的模型差异。
from sklearn.linear_model import Lasso
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
x = scaler.fit_transform(iris.data)
y = iris.target
lasso = Lasso(alpha=0.2)
lasso.fit(x,y)
lasso.coef_
L2正则化将系数向量的L2范数添加到损失函数中,由于L2惩罚项中的系数是二次方的,会让系数的取值变得平均,对于有相关性的变量,会得到相近的系数;L2正则化也较L1稳定;
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Lasso
from sklearn.linear_model import Ridge
iris = load_iris()
#看一下各变量之间的相关性
data = pd.DataFrame(iris.data)
data.corr()
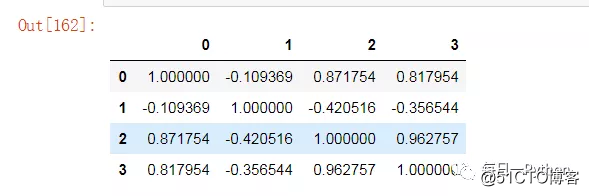
可以看出2和3、0和2、3变量之间有较强的关联性,然后看一下分别使用线性回归、L1正则化和L2正则化后的变量系数:
scaler = StandardScaler()
x = scaler.fit_transform(iris.data)
y = iris.target
lr = LinearRegression()
lr.fit(x,y)
lr.coef_

lasso = Lasso(alpha=0.5)
lasso.fit(x,y)
lasso.coef_

ridge = Ridge(alpha=10)
ridge.fit(x,y)
ridge.coef_

可以看出L1正则化后容易得到一个稀疏矩阵,L2正则化后系数会趋于平均。
3.2树模型
可以利用随机森林或者GBDT模型进行特征选择,之前我有一篇博文讲的这个,这里不再详细说明;上一篇随机森林筛选变量的链接:https://mp.weixin.qq.com/s/6gc3H2y6SnOzdyx_L2WBwg
一)(实现一款简单的接口自动化框架))












.PDF...)
------ redis的五大数据类型实现原理)




