学习【高等数学(上)】6小时从0基础直追满绩!_哔哩哔哩_bilibili
高数基础
高等数学无非分为三个部分:极限、导数(微分)和积分——构成了微积分
高等数学学的就是 微积分,整体其实只是一个思想 + 一个公式(牛顿莱布尼茨公式)
抓住本质(推导圆的面积)
假设当前这样一个圆,我们都知道
- 圆的面积:
π * r^2 - 圆的周长:
π * 直径
我们知道了当前圆的周长,但是我们是怎么知道圆的面积的?!
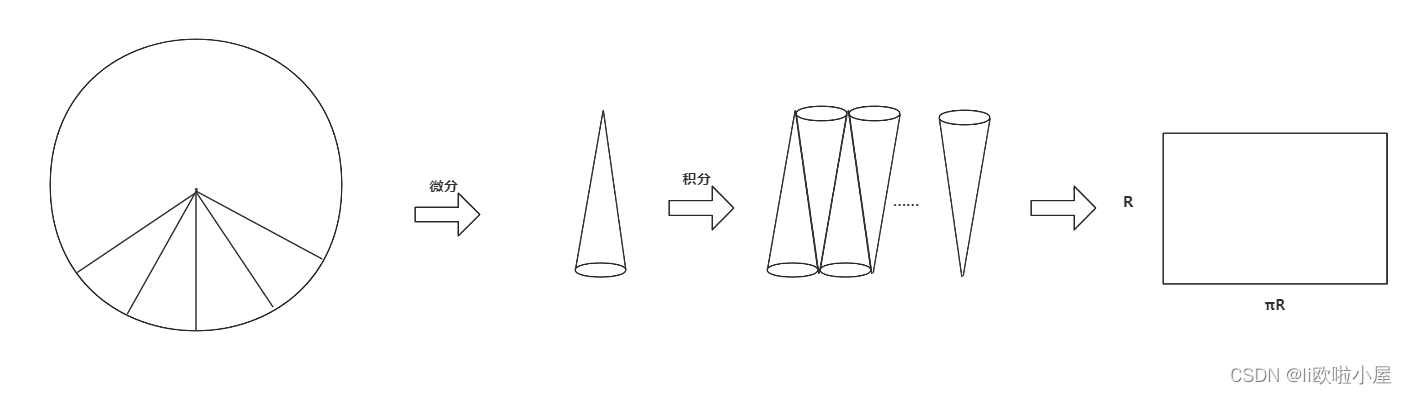
方法一:切割成扇形
我们将一个圆形分割成多个扇形
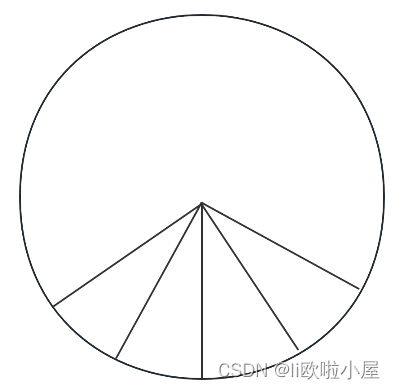
我们取出一个小扇形看看
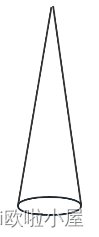
如果我们切割得足够细小的话,那么我们就可以近似看做为一个三角形的面积
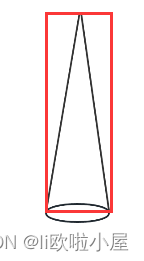
这个面积太小了,我们也没有办法求,也不好求。
我们就可以将这个再次组装起来,但是不要组装成圆,而是按照这一个类型进行组装。
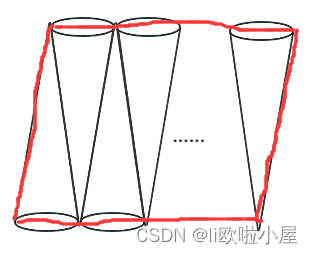
如果我们切割的扇形足够细,那么我们可以近似的认为这个图形为矩形。
- 宽近似于:R
- 长近似于:πR(因为是上下一半,因此并不是2 * π * r)
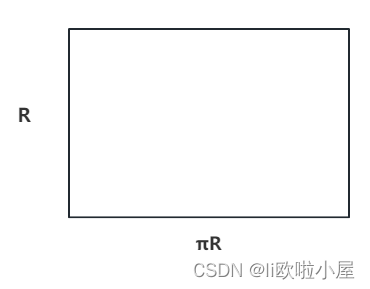
因此面积为:π * R ^ 2
我们拆解成小的,我们可以把握的元素——微分
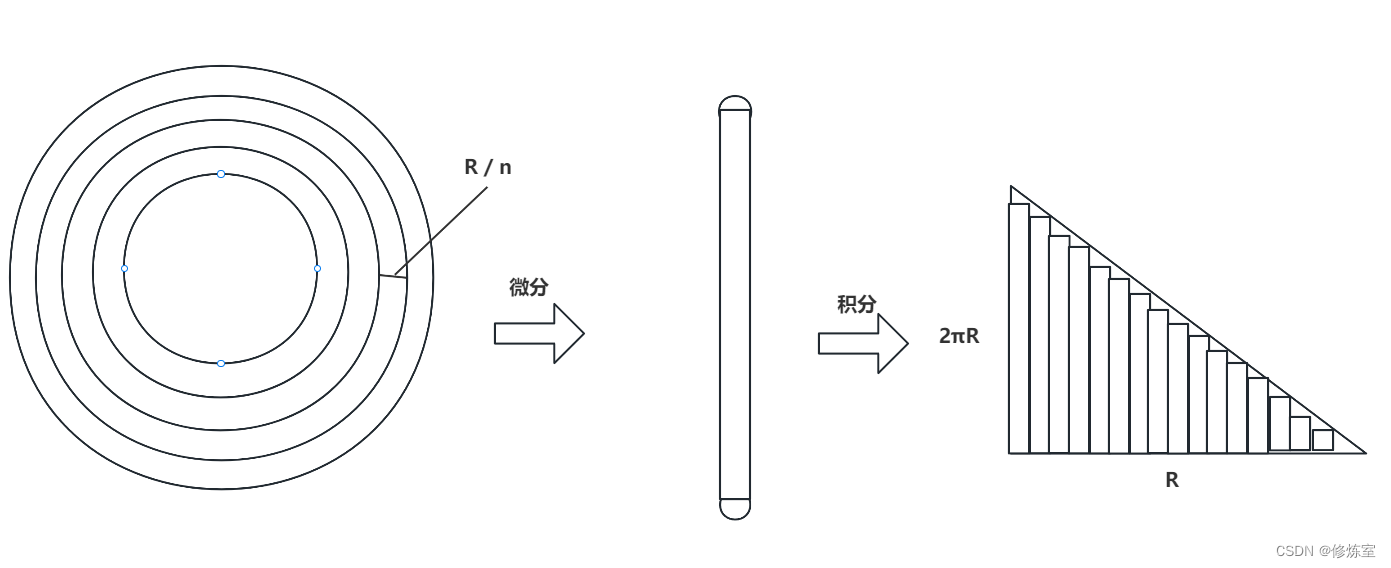
方法二:拆分为圆环
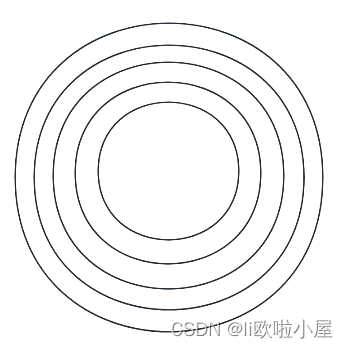
我们将其拆分为小的圆环,如果我们拆分为n分,那么这个小的圆环的宽度就是
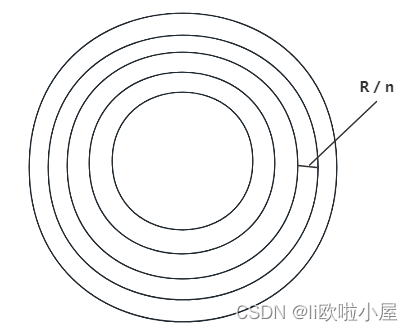
把其中的一个圆环拿出来,那应该怎么进行求解呢?
别拿圆的面积公式直接求,现在我们正在证明圆的面积计算公式
我们拆分出来,就可以得到一个小矩形
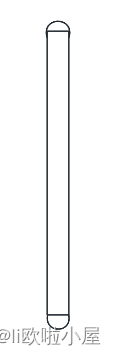
- 长度:圆环周长
- 宽度:R / n
汇总之后就可以得到下面的结果
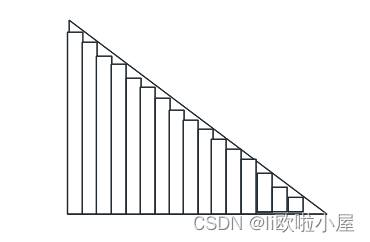
- 最长的长度为:圆形的周长——2 * π * R
- 内部的长度为:半径R(所有的宽度拼接到一起)
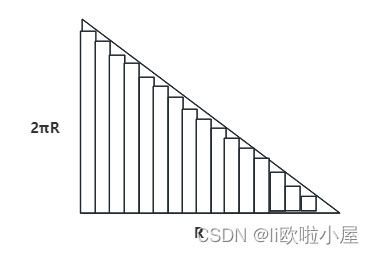
圆形面积:2 π R * R * 1 / 2 = π * R *R
但是这里好像还是存在问题,这里我们在切扇形 还是 圆形的时候,切多少份合适呢?
如果我们切割的无限大,宽度在减小,误差也在减小
问题一:为什么不知道圆的面积公式,但是可以使用圆的周长公式呢?
这里主要是理解微积分的核心思想,使用的是重组面积的方法。
在重组过程中,半径和周长是不变的,因此可以使用(当然这里实际会有误差的)
看起来高等数学都在学微分和积分,那我们为什么要学极限的?
——因为这是他两的
基础啊!
问题二:x趋于0 和 x = 0有什么区别呢?
这是动静之间的差别,x趋于0可以一直在变小的量,是 动态 的,但是x = 0则是一个常量,是一个 静态 的量
(无穷小)极限可以用一句话表示:要多小有多小
如何求解极限
求极限可以简要分成三步:
第一步:代入
将自变量极限值代入极限表达式,如果不能得到结果,继续下一步;
第二步:分类
判断极限类型属于
中的哪一种,
重点是识别出式中的无穷小和无穷大成分
第三步:求解(化形、变形)
特别记住
- 无穷小 * 有界函数= 0
方法一:直接带入型(最简化)
求解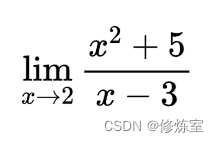
我们可以直接带入,可得
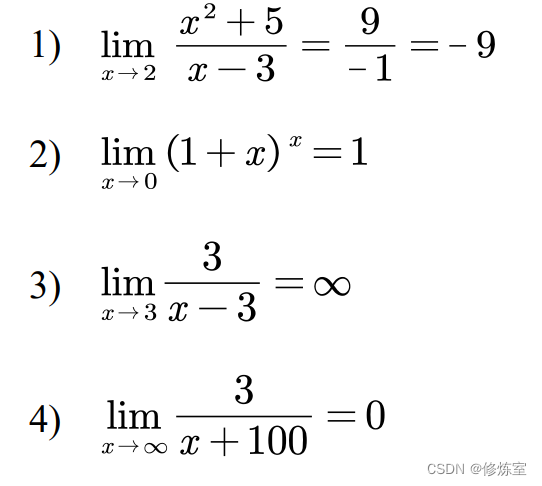
无穷小 * 有界函数= 0
求 的值
直接带入即可得到0
一个无穷小量乘以一个有界函数【-1,1】,结果必然还是一个无穷小量
求解反函数
求 的值
这里需要注意的是,无穷的方向。
若是正无穷,则是 π / 2
若是负无穷,则是 - π / 2
但是,若直接是无穷,则极限不存在
方法二:分类
该方法则专门用于处理 直接带入 无法处理的情况
其实这里主要是由于
无穷小量和无穷大量组成
无穷小
例题:

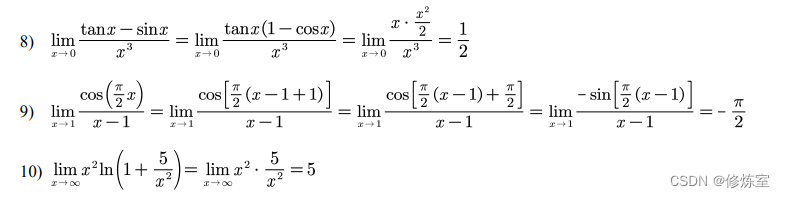
化简
我们发现上面的题目,我们带入值之后就是 0 / 0型,所以需要进行化简
-
第一题,当x --> 2 时,肯定我们可以化简出
x - 2这样的无穷小量;所以两个就可以直接拆解成(x-3)、 (x+2)的式子
在消除x-2之后,就可以再次带入求解了 -
第二题,必然要化简出
x - 1这样的式子;分母很自然的可以进行因式分解,但是第一个就需要借助分子有理化了
代换
主要是记住常用的无穷小的等价代换(只有无穷小才可以换~!)

这里拿
ln(cos x)进行举例,当x趋近于0时,式子当然也趋近于0 ;但是我们需要进行化简方便计算;
当x = 0时,cos x = 1,所以这里如果我们需要构造无穷小量就需要我们 -1 ——即ln(1 + (cos x - 1 ) )
因为ln(1 + x ) ~ x;所以 ~(cos x - 1)
因为 1 - cosx ~ x^2 / 2 ,所以 ~(-x^2 / 2)
补充一个题目:
这里不能直接想当然的用 cosx ~ x,因为这里无法进行下一步求解了。
而是需要我们进行构造
这里需要用到公式
所以可以换成
继续因为sinx ~ x可以换成
所以结果就是:
这里不是什么一眼看出来的,而是明白自己的目的——就是抓出无穷小量来(因为是0 / 0型)——看分母就明白了,无穷小量应该对应的是
x - 1
特别注意的是:不能用于加减法
绝对不能直接替换!!!
而是需要进行 拆解
无穷大


这里注意一下,对于第一题当然可以直接除去x的平方,但是对于下面的例题就需要除以x了(x属于不同范围)
因为这里的x是趋于0的,所以
只需要处理x即可
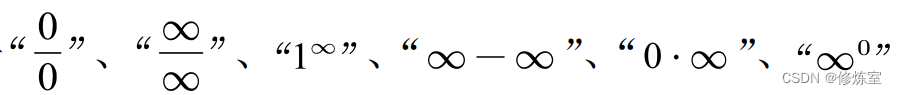

遥感云大数据、洪涝灾害监测、红树林遥感制图、河道轮廓监测、洪涝灾害监测、GRACE重力卫星、源遥感影像)
















)
