写在前面:
在之前的文章当中提到过,学习梯度下降算法,可能需要一点点线性代数的知识。在本篇文章当中,我们的讨论就涉及到了向量。
笔者也曾提到,不妨把向量看成对数据进行批量操作的一种工具,这样可能对我们理解接下来的知识有一些帮助。
推荐阅读:吴恩达机器学习:
第五章:正规方程
第六章:矢量
Outline:
- 矢量
- 正规方程
一.矢量
在我们将向量应用到我们的梯度算法之前我们进行一个简单的回顾。

这是我们的多元函数梯度下降算法。
我们来看一下预测函数的计算在MATLAB/C++中的代码实现(吴恩达老师的课程中对Octave/MATLAB的简单应用进行了讲解,笔者认为大家可以系统的学习Python和MATLAB,这有助于我们接下来的算法实现)



通过上述代码的实现,我们可以看出:相对于未向量化的循环结构,我们向量化之后对数据进行批量操作,两个矩阵的一次乘法运算就可以得到我们的预测值,提高了我们的算法效率。
下面我们展示对梯度下降算法进行矢量化后的结果(这也是一个难点)

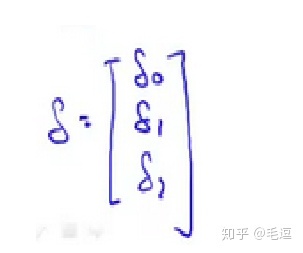
上述表达式中θ是一个列向量,δ也是一个列向量,我们来看看他们具体是什么。
θ:是一个n+1维向量,分量是θ_0到θ_n
δ:
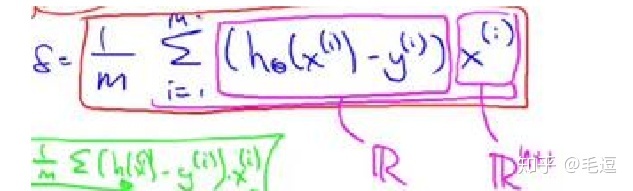
读者可以耐下性子自己动笔计算验证,向量化后的算法跟未向量化的算法是完全等价的,在这里我们对数据进行了批量计算,提高了我们的算法效率。也许对于刚刚接触线性代数的朋友来数,这是难以理解的,但是不要心急,上述计算所具备的知识就是基本的向量加减运算,向量的乘法运算,耐心计算,搞明白上述算法的内涵。
总结一下,我们得到了向量化的梯度下降算法:
二.正规方程组
我们来回顾一下我们求解多元函数代价函数极小值点的数学原理是什么:各个一阶偏导数为零。
除了这样做,我们还有什么办法?
我们来看看正规方程组法求解极小值点。

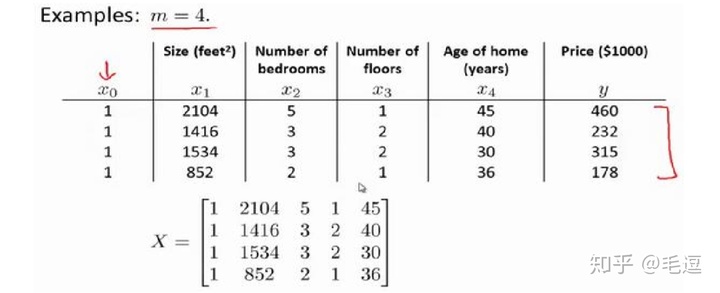
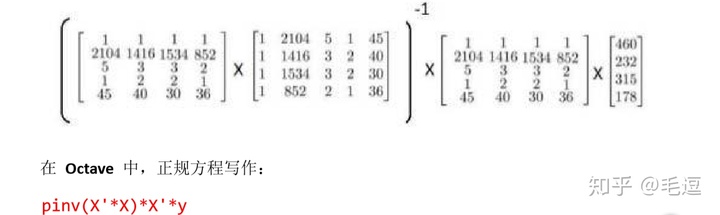
实际上,当特征变量的数目并不大(小于一万)的时候,我们通常采用正规方程组的方法,而不是梯度下降算法。
熟悉线性代数的朋友可能知道,有时候可能会存在矩阵不可逆的情况,我们将这样的矩阵称之为奇异矩阵;但是我们的pinv函数,是一个求伪逆函数,这意味着即使我们的矩阵不可逆,我们的算法仍然可以正常运行。
我们给出正规方程组算法的证明(看懂它需要了解矩阵求导法则)

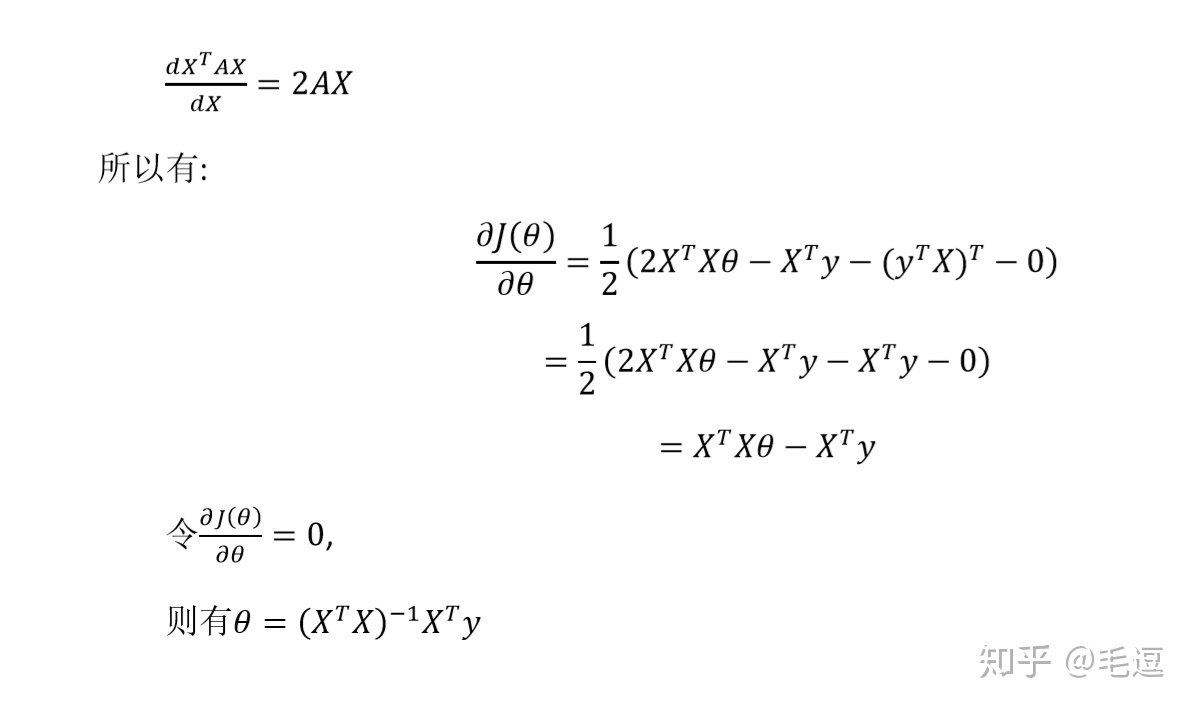
到这篇文章结束为止,我们要对线性回归预测说一声暂时的告别,希望大家可以结合视频学习,自己敲敲代码,实现自己的算法。多练习,多实践。
第一次截稿日期:2019/5/4



















