1.多项式曲线拟合
此示例说明如何使用 polyfit 函数将多项式曲线与一组数据点拟合。您可以按照以下语法,使用 polyfit 求出以最小二乘方式与一组数据拟合的多项式的系数
p = polyfit(x,y,n),
其中:
• x 和 y 是包含数据点的 x 和 y 坐标的向量
• n 是要拟合的多项式的次数
创建包含五个数据点的 x-y 测试数据。
x = [1 2 3 4 5];
y = [5.5 43.1 128 290.7 498.4];
使用 polyfit 求与数据近似拟合的三次多项式。
p = polyfit(x,y,3)
p = 1×4
-0.1917 31.5821 -60.3262 35.3400
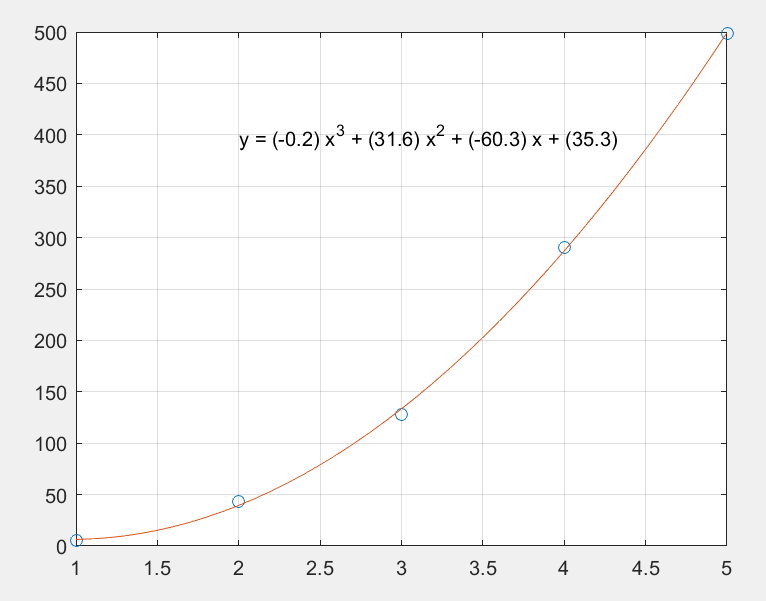
使用 polyfit 获取拟合线的多项式后,可以使用 polyval 计算可能未包含在原始数据中的其他点处的多项式。在更小域内计算 polyfit 估计值,并绘制实际数据值的估计值以进行对比。可以为拟合线包含方程注释。
x2 = 1:.1:5;
y2 = polyval(p,x2);
plot(x,y, 'o' ,x2,y2)
grid on
s = sprintf( 'y = (%.1f) x^3 + (%.1f) x^2 + (%.1f) x + (%.1f)' ,p(1),p(2),p(3),p(4));
text(2,400,s)
1.1 预测美国人口
此示例说明,即使使用次数最适中的多项式外插数据也是有风险且不可靠的。此示例比 MATLAB® 出现得更早。该示例最初作为一个练习出现在 Forsythe、Malcolm 和 Moler 合著的《Computer Methods for Mathematical Computations》一书中,该书由出版商 Prentice-Hall 在1977 年出版。
现在,通过 MATLAB 可以更容易地改变参数和查看结果,但基础数学原理未变。使用 1910 年至 2000 年的美国人口普查数据创建并绘制两个向量。
% Time interval
t = (1910:10:2000)';
% Population
p = [91.972 105.711 123.203 131.669 150.697 ...
179.323 203.212 226.505 249.633 281.422]';
% Plot
plot(t,p, 'bo' );
axis([1910 2020 0 400]);
title( 'Population of the U.S. 1910-2000' );
ylabel( 'Millions' );

那么猜想一下 2010 年美国的人口是多少?
p
p = 10×1
91.9720
105.7110
123.2030
131.6690
150.6970
179.3230
203.2120
226.5050
249.6330
281.4220
将这些数据与 t 中的一个多项式拟合,并使用它将人口数外插到 t = 2010。通过对包含范德蒙矩阵的线性系统求解来获得多项式中的系数,该矩阵为 11×11,其元素为缩放时间的幂,即 A(i,j) = s(i)^(n-j) 。
n = length(t);
s = (t-1950)/50;
A = zeros(n);
A(:,end) = 1;
for j = n-1:-1:1
A(:,j) = s .* A(:,j+1);
end
通过对包含范德蒙矩阵最后 d+1 列的线性系统求解,获得与数据 p 拟合的 d 次多项式的系数 c: A(:,n-d:n)*c ~= p
• 如果 d < 10 ,则方程个数多于未知数个数,并且最小二乘解是合适的。
• 如果 d == 10 ,则可以精确求解方程,而多项式实际上会对数据进行插值。
在任一种情况下,都可以使用反斜杠运算符来求解方程组。三次拟合的系数为:
c = A(:,n-3:n)\p
c = 4×1
-5.7042
27.9064
103.1528
155.1017
现在,计算从 1910 年到 2010 年每一年的多项式,然后绘制结果。
v = (1910:2020)';
x = (v-1950)/50;
w = (2010-1950)/50;
y = polyval(c,x);
z = polyval(c,w);
hold on
plot(v,y, 'k-' );
plot(2010,z, 'ks' );
text(2010,z+15,num2str(z));
hold off

将三次拟合与四次拟合进行比较。请注意,外插点完全不同。
c = A(:,n-4:n)\p;
y = polyval(c,x);
z = polyval(c,w);
hold on
plot(v,y, 'k-' );
plot(2010,z, 'ks' );
text(2010,z-15,num2str(z));
hold off

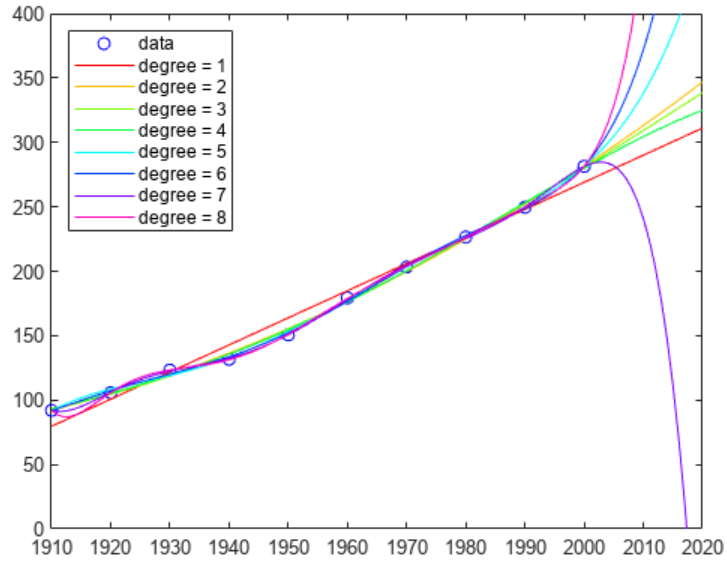
随着阶数增加,外插变得越来越不可靠。
cla
plot(t,p, 'bo' )
hold on
axis([1910 2020 0 400])
colors = hsv(8);
labels = { 'data' };
for d = 1:8
[Q,R] = qr(A(:,n-d:n));
R = R(1:d+1,:);
Q = Q(:,1:d+1);
c = R\(Q'*p); % Same as c = A(:,n-d:n)\p;
y = polyval(c,x);
z = polyval(c,11);
plot(v,y, 'color' ,colors(d,:));
labels{end+1} = [ 'degree = ' int2str(d)];
end
legend(labels, 'Location' , 'NorthWest' )
hold off
2.标量函数的根
2.1 对一元非线性方程求解
fzero 函数尝试求一个一元方程的根。可以通过用于指定起始区间的单元素起点或双元素向量调用该函数。如果为 fzero 提供起点 x0 , fzero 将首先搜索函数更改符号的点周围的区间。如果找到该区间,fzero 返回函数更改符号的位置附近的值。如果未找到此类区间, fzero 返回 NaN。或者,如果知道函数值的符号不同的两个点,可以使用双元素向量指定该起始区间; fzero 保证缩小该区间并返回符号更改处附近的值。
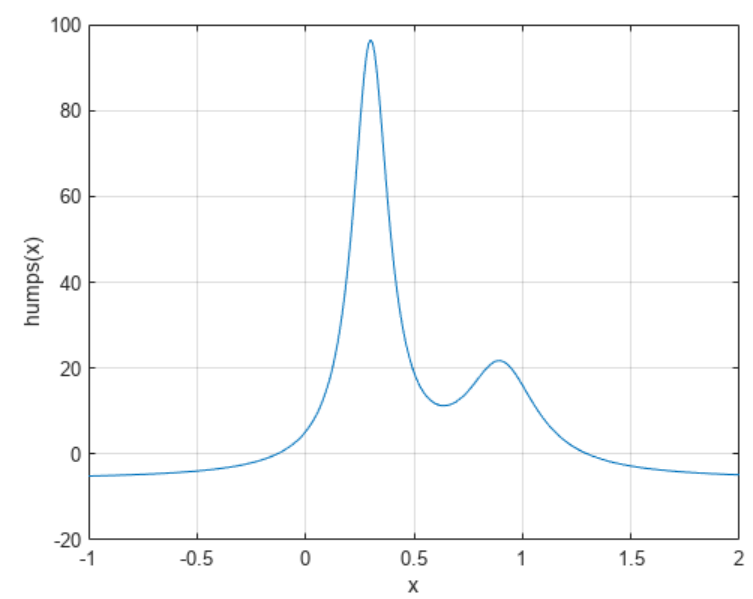
以下部分包含两个示例,用于说明如何使用起始区间和起点查找函数的零元素。这些示例使用由MATLAB® 提供的函数 humps.m 。下图显示了 humps 的图。
x = -1:.01:2;
y = humps(x);
plot(x,y)
xlabel( 'x' );
ylabel( 'humps(x)' )
grid on
2.2 为 fzero 设置选项
可以通过设置选项控制 fzero 函数的多个方面。使用 optimset 设置选项。选项包括:
• 选择 fzero 生成的显示量 - 请参阅“设置优化选项” 、使用起始区间和使用起点。
• 选择控制 fzero 如何确定它得到根的不同公差 - 请参阅“设置优化选项” 。
• 选择用于观察 fzero 逼近根的进度的绘图函数 - 请参阅“优化求解器绘制函数” 。
• 使用自定义编程的输出函数观察 fzero 逼近根的进度 - 请参阅“优化求解器输出函数” 。
2.3 使用起始区间
humps 的图指示 x = -1 时函数为负数, x = 1 时函数为正数。可以通过计算这两点的 humps 进行确认。
humps(1)
ans = 16
humps(-1)
ans = -5.1378
因此,可以将 [-1 1] 用作 fzero 的起始区间。fzero 的迭代算法可求 [-1 1] 越来越小的子区间。对于每个子区间, humps 在两个端点的符号不同。由于子区间的端点彼此越来越近,因此它们收敛到 humps 的零位置。要显示 fzero 在每个迭代过程中的进度,请使用 optimset 函数将 Display 选项设置为 iter 。
options = optimset( 'Display' , 'iter' );
然后如下所示调用 fzero :
a = fzero(@humps,[-1 1],options)
Func-count x f(x) Procedure
2 -1 -5.13779 initial
3 -0.513876 -4.02235 interpolation
4 -0.513876 -4.02235 bisection
5 -0.473635 -3.83767 interpolation
6 -0.115287 0.414441 bisection
7 -0.115287 0.414441 interpolation
8 -0.132562 -0.0226907 interpolation
9 -0.131666 -0.0011492 interpolation
10 -0.131618 1.88371e-07 interpolation
11 -0.131618 -2.7935e-11 interpolation
12 -0.131618 8.88178e-16 interpolation
13 -0.131618 8.88178e-16 interpolation
Zero found in the interval [-1, 1]
a = -0.1316
每个值 x 代表迄今为止最佳的端点。 Procedure 列向您显示每步的算法是使用对分还是插值。可以通过输入以下内容验证 a 中的函数值是否接近零:
humps(a)
ans = 8.8818e-16
2.4 使用起点
假定您不知道 humps 的函数值符号不同的两点。在这种情况下,可以选择标量 x0 作为 fzero 的起点。fzero 先搜索函数更改符号的点附近的区间。如果 fzero 找到此类区间,它会继续执行上一部分中介绍的算法。如果未找到此类区间, fzero 返回 NaN。
例如,将起点设置为 -0.2 ,将 Display 选项设置为 Iter ,并调用 fzero :
options = optimset( 'Display' , 'iter' );
a = fzero(@humps,-0.2,options)
Search for an interval around -0.2 containing a sign change:
Func-count a f(a) b f(b) Procedure
1 -0.2 -1.35385 -0.2 -1.35385 initial interval
3 -0.194343 -1.26077 -0.205657 -1.44411 search
5 -0.192 -1.22137 -0.208 -1.4807 search
7 -0.188686 -1.16477 -0.211314 -1.53167 search
9 -0.184 -1.08293 -0.216 -1.60224 search
11 -0.177373 -0.963455 -0.222627 -1.69911 search
13 -0.168 -0.786636 -0.232 -1.83055 search
15 -0.154745 -0.51962 -0.245255 -2.00602 search
17 -0.136 -0.104165 -0.264 -2.23521 search
18 -0.10949 0.572246 -0.264 -2.23521 search
Search for a zero in the interval [-0.10949, -0.264]:
Func-count x f(x) Procedure
18 -0.10949 0.572246 initial
19 -0.140984 -0.219277 interpolation
20 -0.132259 -0.0154224 interpolation
21 -0.131617 3.40729e-05 interpolation
22 -0.131618 -6.79505e-08 interpolation
23 -0.131618 -2.98428e-13 interpolation
24 -0.131618 8.88178e-16 interpolation
25 -0.131618 8.88178e-16 interpolation
Zero found in the interval [-0.10949, -0.264]
a = -0.1316
每个迭代中当前子区间的端点列在标题 a 和 b 下,而端点处的相应 humps 值分别列在 f(a) 和 f(b) 下。
注意:端点 a 和 b 未按任何特定顺序列出: a 可能大于 b 或小于 b 。
对于前 9 步,humps 的符号在当前子区间的两端点都为负号,如输出中所示。在第 10 步, humps 的符号在 a ( -0.10949 ) 处为正号,但在 b ( -0.264) 处为负号。从该点开始,如上一部分中所述,算法继续缩小区间 [-0.10949 -0.264] ,直到它达到值 -0.1316 。


)
生成)











n种讨论 JAVA)
】字符串 | 二进制类型)


