读完本文,你可以去力扣拿下如下题目:
56.合并区间
-----------
上篇文章用贪心算法解决了区间调度问题:给你很多区间,让你求其中的最大不重叠子集。
其实对于区间相关的问题,还有很多其他类型,本文就来讲讲区间合并问题(Merge Interval)。
LeetCode 第 56 题就是一道相关问题,题目很好理解:

我们解决区间问题的一般思路是先排序,然后观察规律。
PS:我认真写了 100 多篇原创,手把手刷 200 道力扣题目,全部发布在 labuladong的算法小抄,持续更新。建议收藏,按照我的文章顺序刷题,掌握各种算法套路后投再入题海就如鱼得水了。
一、思路
一个区间可以表示为 [start, end],前文聊的区间调度问题,需要按 end 排序,以便满足贪心选择性质。而对于区间合并问题,其实按 end 和 start 排序都可以,不过为了清晰起见,我们选择按 start 排序。
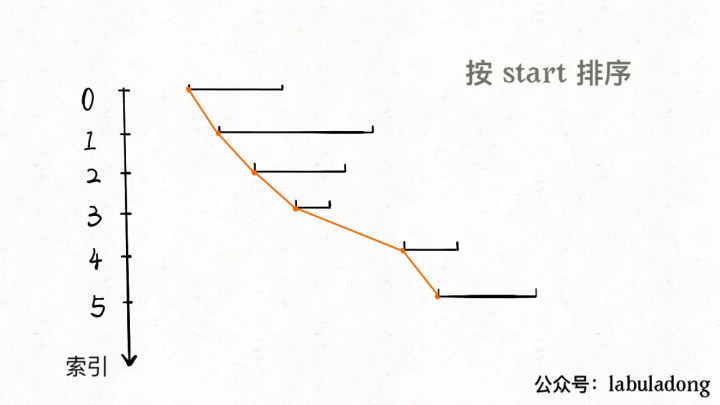
显然,对于几个相交区间合并后的结果区间 x,x.start 一定是这些相交区间中 start 最小的,x.end 一定是这些相交区间中 end 最大的。
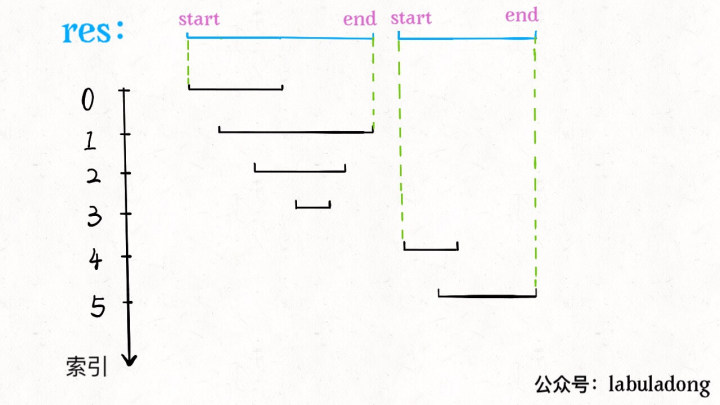
由于已经排了序,x.start 很好确定,求 x.end 也很容易,可以类比在数组中找最大值的过程:
int max_ele = arr[0];
for (int i = 1; i < arr.length; i++) max_ele = max(max_ele, arr[i]);
return max_ele;
二、代码
# intervals 形如 [[1,3],[2,6]...]
def merge(intervals):if not intervals: return []# 按区间的 start 升序排列intervals.sort(key=lambda intv: intv[0])res = []res.append(intervals[0])for i in range(1, len(intervals)):curr = intervals[i]# res 中最后一个元素的引用last = res[-1]if curr[0] <= last[1]:# 找到最大的 endlast[1] = max(last[1], curr[1])else:# 处理下一个待合并区间res.append(curr)return res
看下动画就一目了然了:
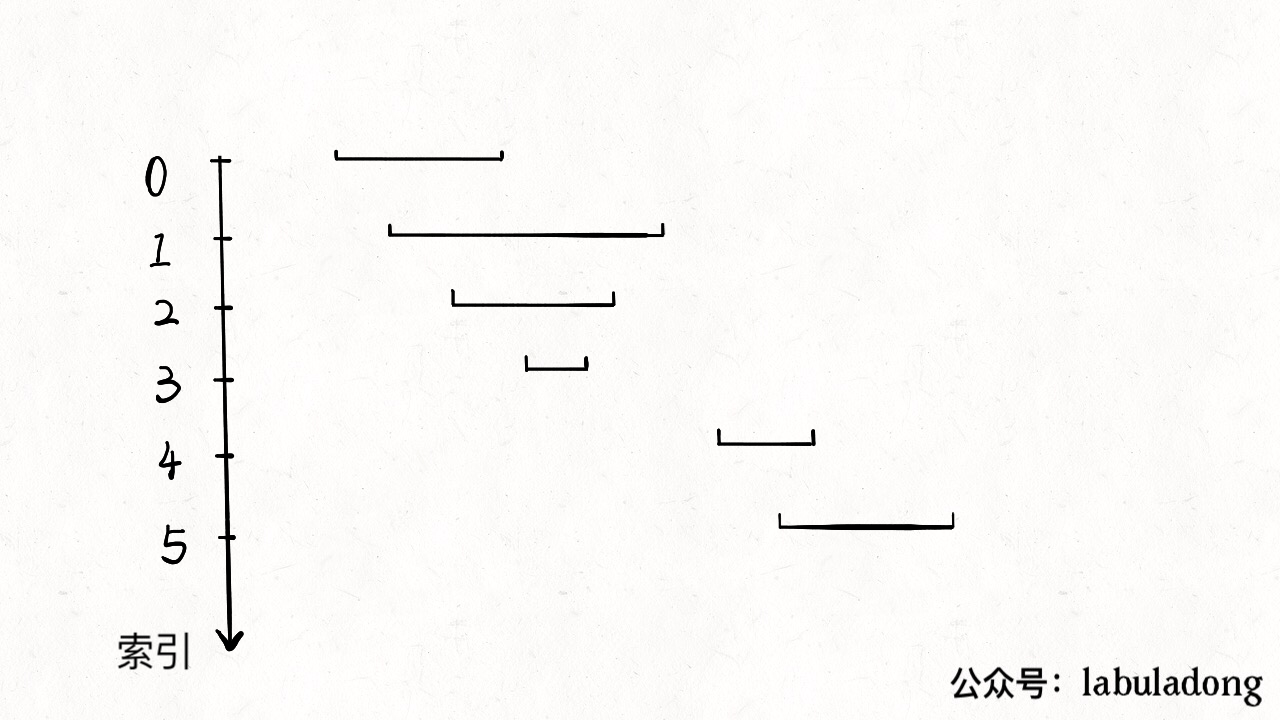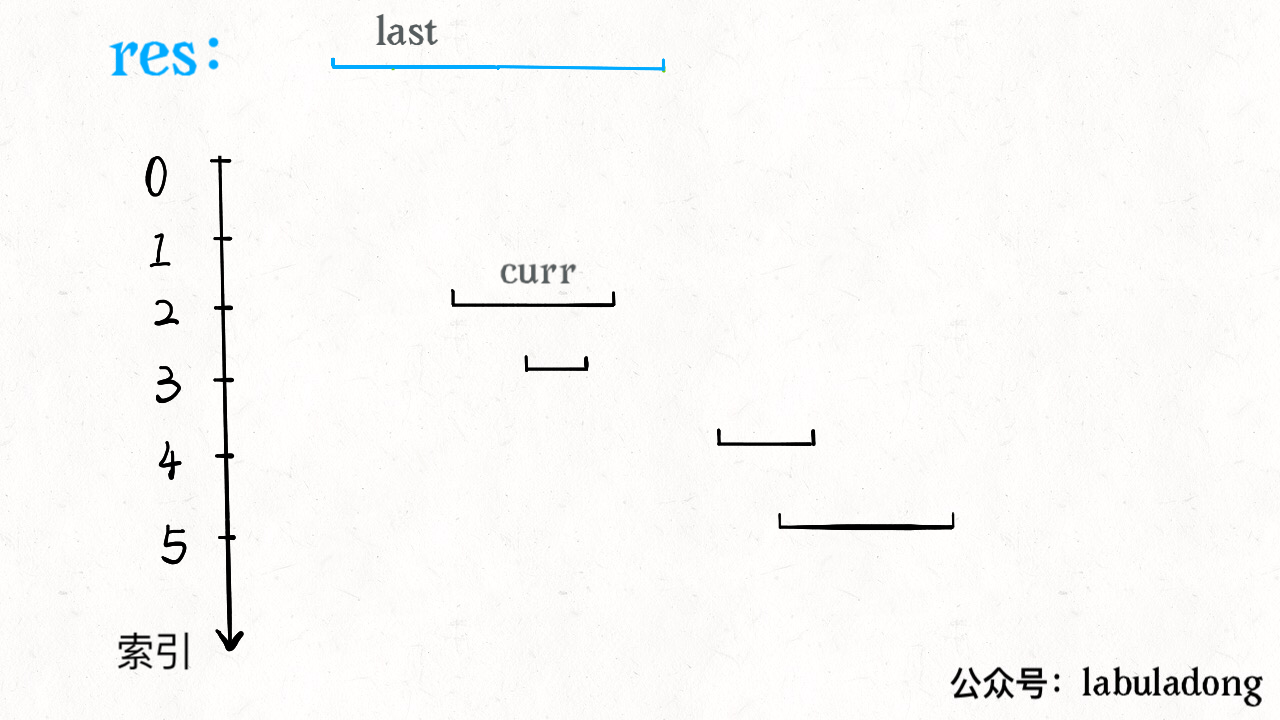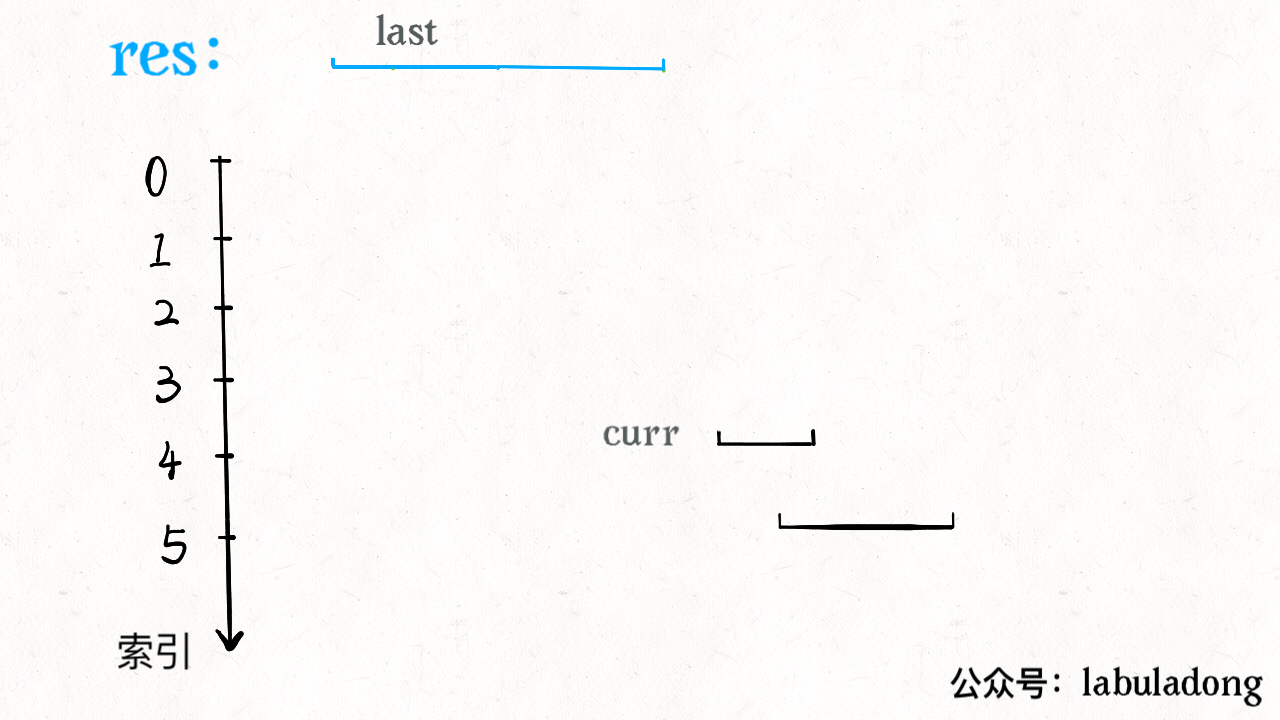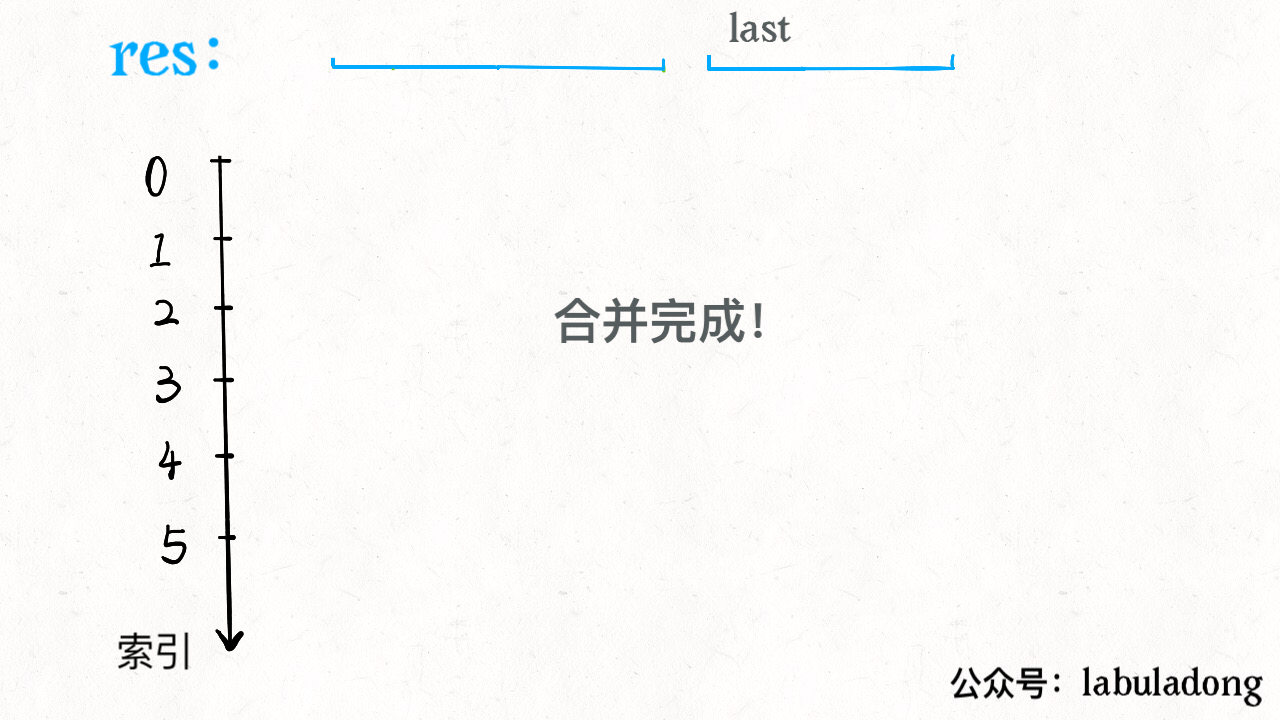
至此,区间合并问题就解决了。本文篇幅短小,因为区间合并只是区间问题的一个类型,后续还有一些区间问题。本想把所有问题类型都总结在一篇文章,但有读者反应,长文只会收藏不会看… 所以还是分成小短文吧,读者有什么看法可以在留言板留言交流。
本文终,希望对你有帮助。
_____________
我的 在线电子书 有 100 篇原创文章,手把手带刷 200 道力扣题目,建议收藏!对应的 GitHub 算法仓库 已经获得了 70k star,欢迎标星!



















