勾股数
![]()
是指满足
![]()
的正整数,它们的通用公式为
![]()
,下边我从定义出发,利用平方差公式举例实验找规律,推导出这一通用公式。
由
![]()
可知
当
![]()
为奇数时
![]()
和
![]()
全都是奇数;当
![]()
为偶数时
![]()
和
![]()
全都是偶数。(
![]()
,与
![]()
同奇同偶)
![]()
当
![]()
时,
![]()
,
![]()
,则
![]()
,
![]()
,此时
![]()
是奇数,令
![]()
,则
![]()
,
![]()
。
由此可得到(3,4,5)(5,12,13)(7,24,25)(9,40,41)(11,60,61)(13,84,85)等勾股数组。
![]()
当
![]()
时,
![]()
,
![]()
,则
![]()
,
![]()
,此时
![]()
是偶数,令
![]()
,则
![]()
,
![]()
。
由此可得到(4,3,5)(6,8,10)(8,15,17)(10,24,26)(12,35,37)(14,48,50)(16,63,65)等勾股数组。
![]()
当
![]()
时,
![]()
,则
![]()
,
![]()
,此时
![]()
是3的倍数且是奇数,令
![]()
,则
![]()
,
![]()
。
由此可得到(9,12,15)(15,36,39)(21,72,75)(27,240,243)(33,180,183)(39,252,255))等勾股数组
...........
发现规律了吗?让我们来一个更直接的假设吧:
![]()
,设
![]()
,则
![]()
,
![]()
,求出
![]()
,
![]()
,即
![]()
,这可以解释为:对任意正整数a和不大于a的每一个正整数k,总是存在两个差为k的有理数,它们的平方差等于a²。
把
![]()
乘上去,得到
![]()
,这就是通用勾股数公式的形式,完毕。
让我们从头分析一下,
![]()
这一式子中有三个变量,一个约束条件,意味着只有两个独立变量,取成a和b,那么推导过程中独立变量是怎么变成a和k的呢?就在于令
![]()
时,以k取代了b。然后我们确定这个等式的通用公式用两个独立变量就可以表示,因此我们有两个独立变量后可以暴力表示,再把有理式化成等式,就可以得到一个通用公式,但这个过程中,a的含义不知不觉发生了变化。
采用相同步骤,还可以寻找
![]() 的通用公式
的通用公式:将式子改写成
![]()
,令
![]()
,则
![]()
,
![]()
,解得
![]()
,
![]()
,即
![]()
,把
![]()
提到分子上后得到了最终公式
![]()
,a、b、k三个独立变量可取任意正整数。
例如,
![]()
时能得到
![]()
;取(3,2,1) 时能得到
![]()
,可继续化简为
![]()
;取(4,2,1) 时能得到
![]()
;取(4,2,3) 时能得到
![]()
;取(2,2,3) 时能得到
![]()
;取(2,2,1) 时能得到
![]()
等。
性质:1.此公式中a与b地位完全对等;
2.左边已经有了两个偶数,为了避免剩下的两个也是偶数,a、b、k中必须有1或3个奇数。
注意到这个公式无法直接生成勾股数嵌套的最简例子
![]()
,因为13、7这些数无法写成三正整数平方和,只能由(3,4,1)生成它的两倍式
![]()
,因此这个公式还是有些粗糙,可能不是最终的通用公式,但已经可以用一下了。
3.(a,b,k)的轮换能产生三种不同的三平方和,
例(5,3,1)(5,1,3)(3,1,5)轮换能导出
![]()
;
(6,2,1)(6,1,2)(2,1,6)轮换能导出
![]()
。
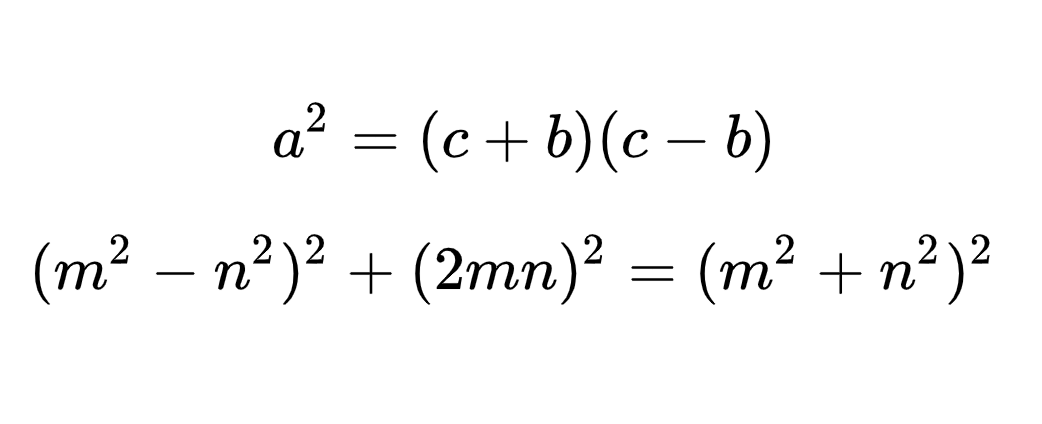

;设p1指向字符串s)














,该函数能将一个十进制数n转换成二进制数,输入13 输出 1101。在main函数中输入整数n,调用函数,输出它的二进制)


