敏捷在软件开发过程中是一个非常著名的术语,它背后的基本思想很简单:快速构建一些东西,然后得到一些反馈,根据反馈做出改变,重复此过程。目标是让产品更贴合用,让用户做出反馈,以获得设计开发出的产品与优秀的产品二者之间误差最小,梯度下降算法背后的原理和这基本一样。
目的
梯度下降算法是一个迭代过程,它将获得函数的最小值。下面的公式将整个梯度下降算法汇总在一行中。

但是这个公式是如何得出的呢?实际上很简单,只需要具备一些高中的数学知识即可理解。本文将尝试讲解这个公式,并以线性回归模型为例,构建此类公式。
机器学习模型
- 考虑二维空间中的一堆数据点。假设数据与一组学生的身高和体重有关。试图预测这些数量之间的某种关系,以便我们可以预测一些新生的体重。这本质上是一种有监督学习的简单例子。
- 现在在空间中绘制一条穿过其中一些数据点的任意直线,该直线方程的形如
Y=mX+b,其中m是斜率,b是其在Y轴的截距。

预测
给定一组已知的输入及其相应的输出,机器学习模型试图对一组新的输入做出一些预测。

两个预测之间的差异即为错误。

这涉及成本函数或损失函数的概念(cost function or loss function)。
成本函数
成本函数/损失函数用来评估机器学习算法的性能。二者的区别在于,损失函数计算单个训练示例的错误,而成本函数是整个训练集上错误的平均值。
成本函数基本上能告诉我们模型在给定m和b的值时,其预测能“有多好”。
比方说,数据集中总共有N个点,我们想要最小化所有N个数据点的误差。因此,成本函数将是总平方误差,即
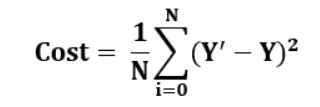
为什么采取平方差而不是绝对差?因为平方差使得导出回归线更容易。实际上,为了找到这条直线,我们需要计算成本函数的一阶导数,而计算绝对值的导数比平方值更难。
最小化成本函数
任何机器学习算法的目标都是最小化成本函数。
这是因为实际值和预测值之间的误差对应着表示算法在学习方面的性能。由于希望误差值最小,因此尽量使得那些m和b值能够产生尽可能小的误差。
如何最小化一个任意函数?
仔细观察上述的成本函数,其形式为Y=X²。在笛卡尔坐标系中,这是一个抛物线方程,用图形表示如下:

为了最小化上面的函数,需要找到一个x,函数在该点能产生小值Y,即图中的红点。由于这是一个二维图像,因此很容易找到其最小值,但是在维度比较大的情况下,情况会更加复杂。对于种情况,需要设计一种算法来定位最小值,该算法称为梯度下降算法(Gradient Descent)。
梯度下降
梯度下降是优化模型的方法中最流行的算法之一,也是迄今为止优化神经网络的最常用方法。它本质上是一种迭代优化算法,用于查找函数的最小值。
表示
假设你是沿着下面的图表走,目前位于曲线'绿'点处,而目标是到达最小值,即红点位置,但你是无法看到该最低点。

可能采取的行动:
- 可能向上或向下;
- 如果决定走哪条路,可能会采取更大的步伐或小的步伐来到达目的地;
从本质上讲,你应该知道两件事来达到最小值,即走哪条和走多远。
梯度下降算法通过使用导数帮助我们有效地做出这些决策。导数是来源于积分,用于计算曲线特定点处的斜率。通过在该点处绘制图形的切线来描述斜率。因此,如果能够计算出这条切线,可能就能够计算达到最小值的所需方向。
最小值
在下图中,在绿点处绘制切线,如果向上移动,就将远离最小值,反之亦然。此外,切线也能让我们感觉到斜坡的陡峭程度。

蓝点处的斜率比绿点处的斜率低,这意味着从蓝点到绿点所需的步长要小得多。
成本函数的数学解释
现在将上述内容纳入数学公式中。在等式y=mX+b中,m和b是其参数。在训练过程中,其值也会发生微小变化,用δ表示这个小的变化。参数值将分别更新为m = m-δm 和b = b-δb。最终目标是找到m和b的值,以使得y=mx+b 的误差最小,即最小化成本函数。
重写成本函数:

想法是,通过计算函数的导数/斜率,就可以找到函数的最小值。
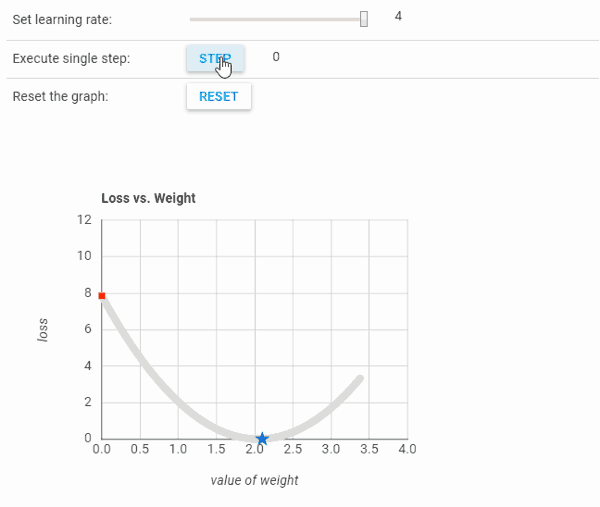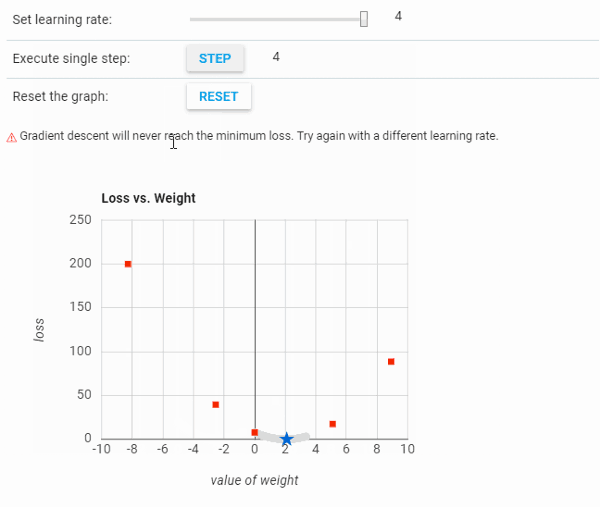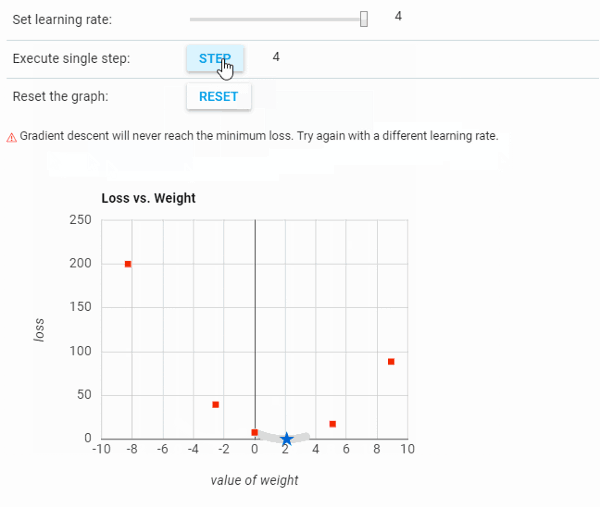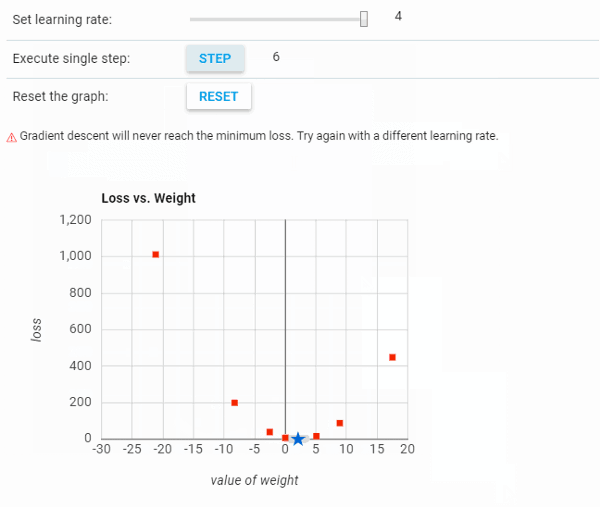
学习率
达到最小值或最低值所采取的步长大小称为学习率。学习率可以设置的比较大,但有可能会错过最小值。而另一方面,小的学习率将花费大量时间训练以达到最低点。
下面的可视化给出了学习率的基本概念。在第三个图中,以最小步数达到最小点,这表明该学习率是此问题的最佳学习率。

从上图可以看到,当学习率太低时,需要花费很长训练时间才能收敛。而另一方面,当学习率太高时,梯度下降未达到最小值,如下面所示:
导数
机器学习在优化问题中使用导数。梯度下降等优化算法使用导数来决定是增加还是减少权重,进而增加或减少目标函数。
如果能够计算出函数的导数,就可以知道在哪个方向上能到达最小化。
主要处理方法源自于微积分中的两个基本概念:
- 指数法则
指数法则求导公式:

- 链式法则
链式法则用于计算复合函数的导数,如果变量z取决于变量y,且它本身也依赖于变量x,因此y和z是因变量,那么z对x的导数也与y有,这称为链式法则,在数学上写为:
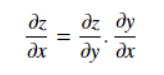
举个例子加强理解:

使用指数法则和链式发规,计算成本函数相对于m和c的变化方式。这涉及偏导数的概念,即如果存在两个变量的函数,那么为了找到该函数对其中一个变量的偏导数,需将另一个变量视为常数。举个例子加强理解:

计算梯度下降
现在将这些微积分法则的知识应用到原始方程中,并找到成本函数的导数,即m和b。修改成本函数方程:
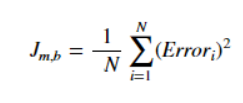
为简单起见,忽略求和符号。求和部分其实很重要,尤其是随机梯度下降(SGD)与批量梯度下降的概念。在批量梯度下降期间,我们一次查看所有训练样例的错误,而在SGD中一次只查看其中的一个错误。这里为了简单起见,假设一次只查看其中的一个错误:

现在计算误差对m和b的梯度:

将值对等到成本函数中并将其乘以学习率:

其中这个等式中的系数项2是一个常数,求导时并不重要,这里将其忽略。因此,最终,整篇文章归结为两个简单的方程式,它们代表了梯度下降的方程。

其中m¹,b¹是下一个位置的参数;m⁰,b⁰是当前位置的参数。
因此,为了求解梯度,使用新的
m和b值迭代数据点并计算偏导数。这个新的梯度会告诉我们当前位置的成本函数的斜率以及我们应该更新参数的方向。另外更新参数的步长由学习率控制。
结论
本文的重点是展示梯度下降的基本概念,并以线性回归为例讲解梯度下降算法。通过绘制最佳拟合线来衡量学生身高和体重之间的关系。但是,这里为了简单起见,举的例子是机器学习算法中较简单的线性回归模型,读者也可以将其应用到其它机器学习方法中。
原文链接
本文为云栖社区原创内容,未经允许不得转载。










...)




原装出厂Windows11系统21H2)



