目录
一.引言
二.堆与二叉堆介绍
1.Heap 堆
2.Binary Heap 二叉堆
3.HeapifyUp 添加节点
4.HeapifyDown 删除节点
5.Heap 时间复杂度
6.Insert & Delete 代码实现
三.经典算法实战
1.Smallest-K [M14]
2.Sliding-Window-Max [239]
3.Ugly-Number [264]
4.Top-K-Freq-Ele [347]
四.总结
一.引言
前面介绍了树和二叉树的概念,接下来介绍 Heap 堆和 Binary Heap 二叉堆,这里堆是一个抽象的数据结构,二叉堆只是其实现的一种形式,并不代表所有堆都使用二叉树实现。
二.堆与二叉堆介绍
1.Heap 堆

堆主要分为两种表现形式,最大堆 or 最小堆,也有叫大根堆 or 小根堆的,其可以在常数时间 o(1) 获取到最大 or 最小的元素,其一般包含 3 个基础 API:
◆ find-max - 寻找堆中的最大值
◆ delete-max - 删除堆中的最大值
◆ insert - 向堆中插入一个新元素
注意 📢 delete 和 insert 操作都会导致堆的结构破坏,所以需要重新调整父子节点位置从而维护堆的原始性质。
2.Binary Heap 二叉堆

二叉堆是基于二叉树实现的 Heap,不过有一点需要注意这里的二叉树是完全二叉树,假设其深度为 h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。也就是除了最后一层叶子 🍃 节点外,其余层的节点都是满的且没有 None。 同时二叉堆一般基于 List 实现,以下述列表为例:
[110, 100, 90, 40, 80, 20, 60, 10, 30, 50, 70]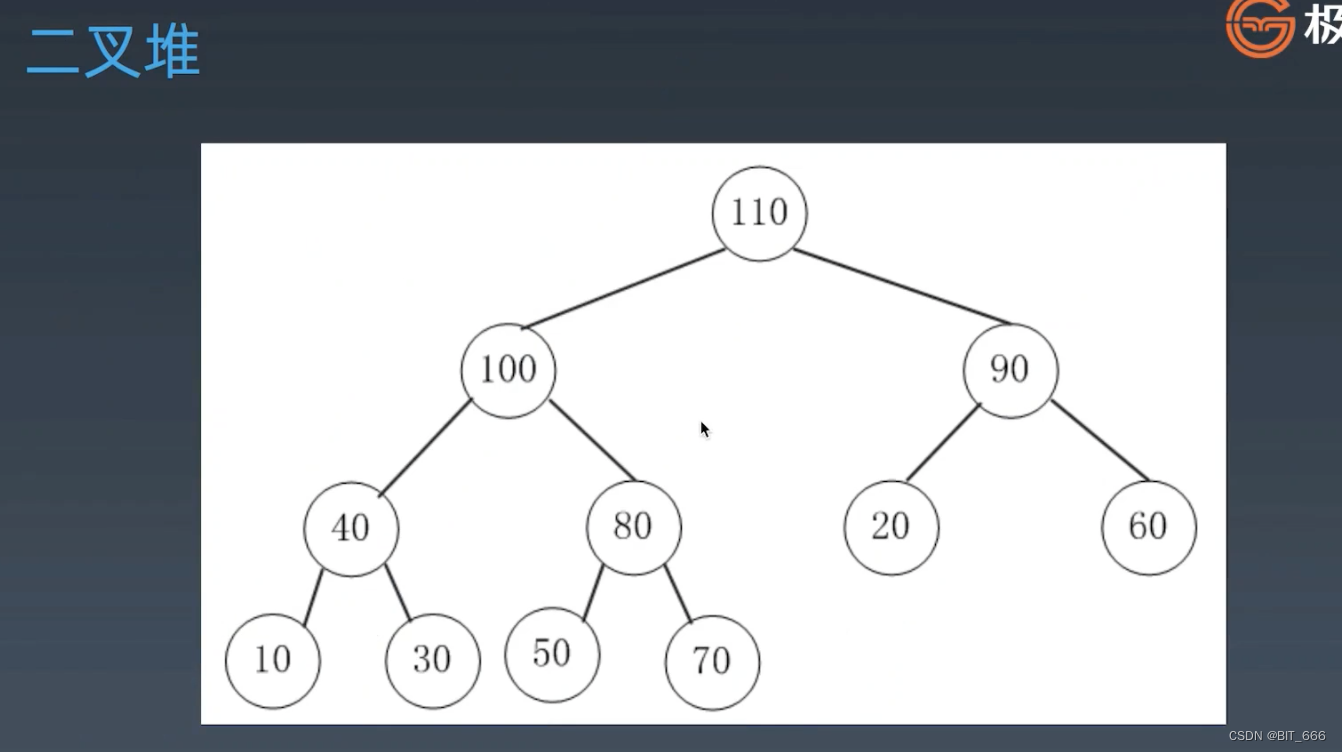
完全二叉树可以看作是满二叉树从尾部叶子节点开始清退,即数组尾部清退,剩下的都是满足完全二叉树的,这样做主要是为了提高效率,如果过多节点为 None,二叉树的深度 h 增加,那么搜索的时间复杂度也会逐渐增加且浪费空间。 基于完全二叉树形态,其具备以下性质:

通过索引 i 我们可以获取对应索引的左右孩子节点和父节点的位置 [如果有的话],假设是 k 叉树的话,索引 i 的 k 个孩子索引为 k*i + 1、k*i + 2、k*i+3 以此类推,父节点索引则为 floor((i-1)/k)。
3.HeapifyUp 添加节点

基于二叉堆 index 及其父子节点的关系,insert 操作首先将节点插入数组尾部,然后依次与父节点比较向上移动直到无法移动,增加元素结束。
◆ 插入 85 到 Heap
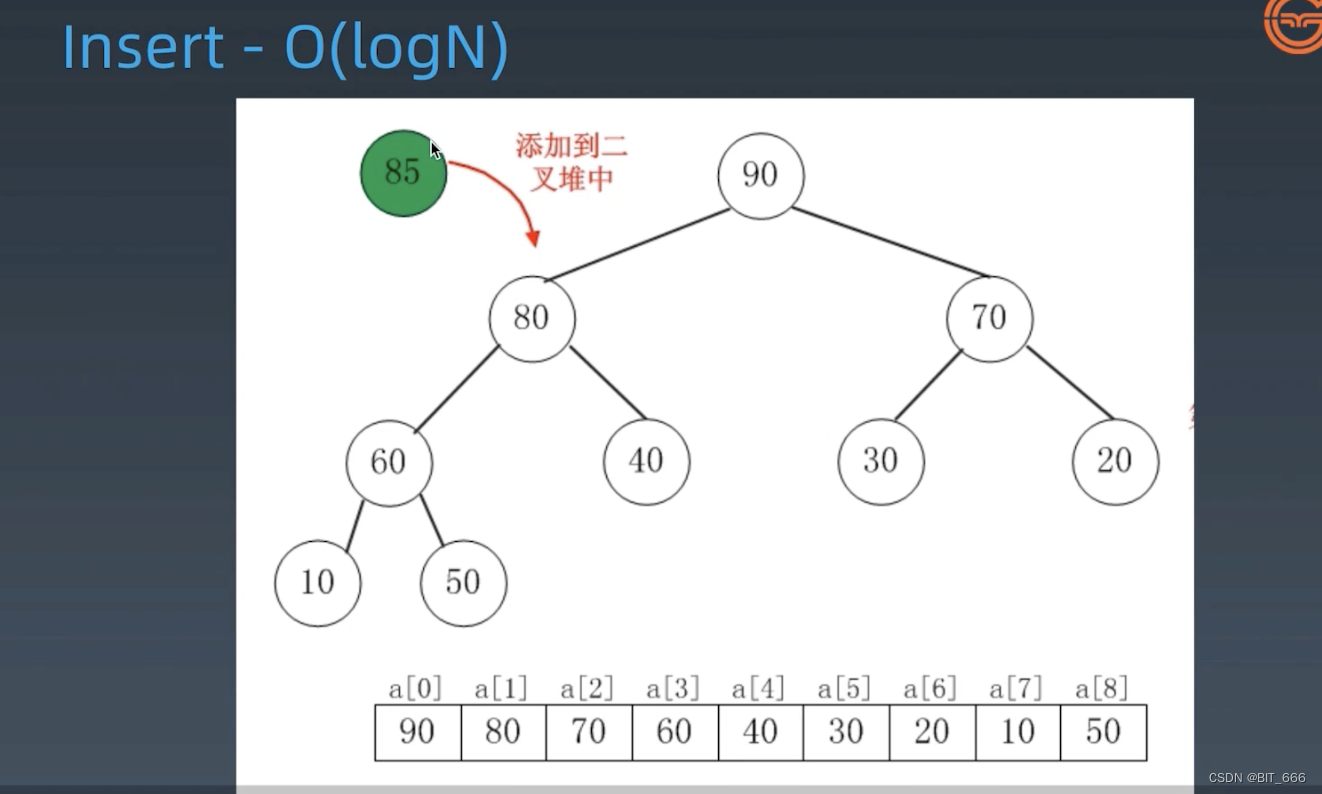
◆ 元素添加到队尾
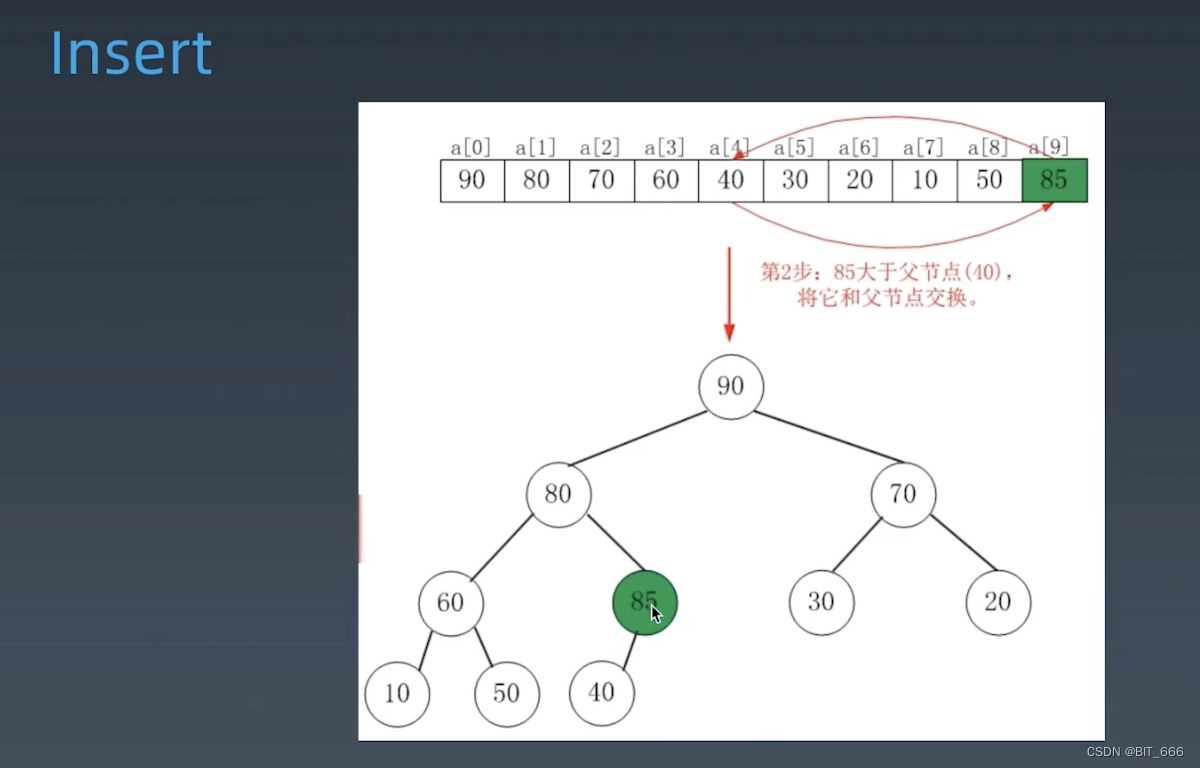
◆ 持续向上移动并交换
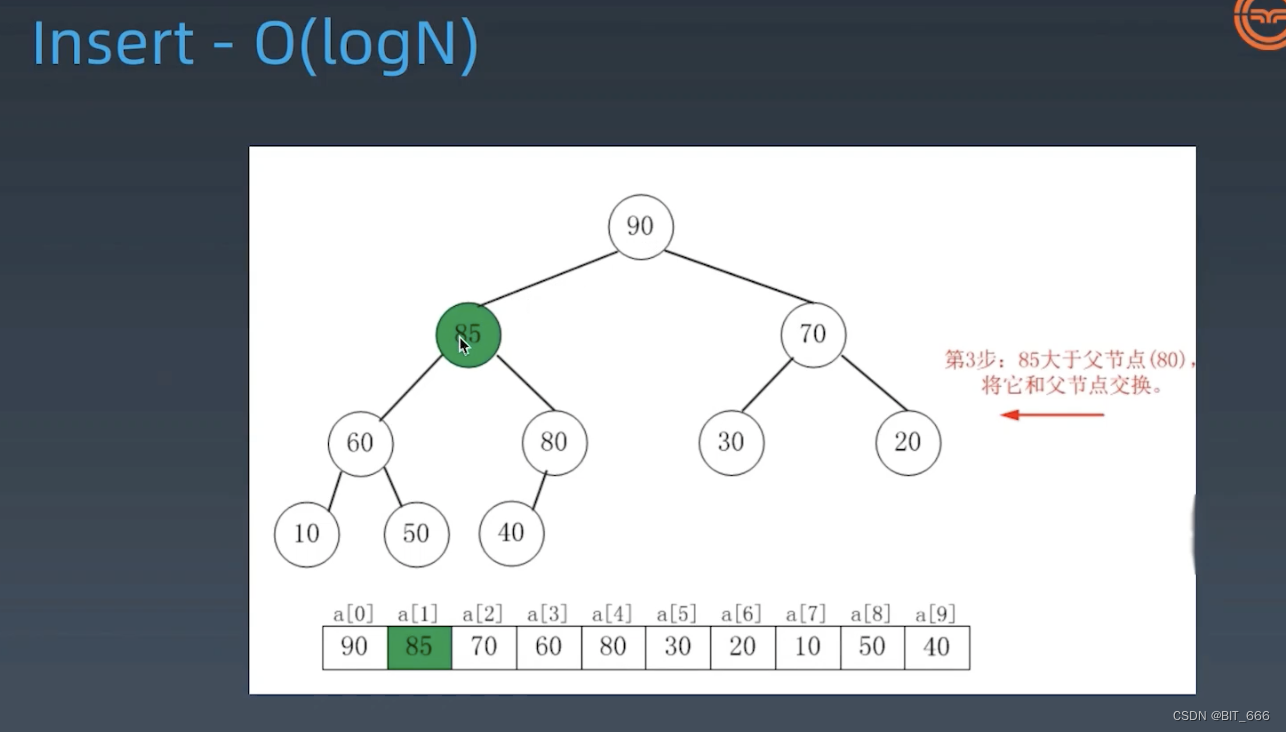
4.HeapifyDown 删除节点

删除元素首先将 root 节点移出,随后将尾节点替换至 root,与左右节点中较大的节点替换位置,如此循环下去,直到不能移动并恢复堆的性质。
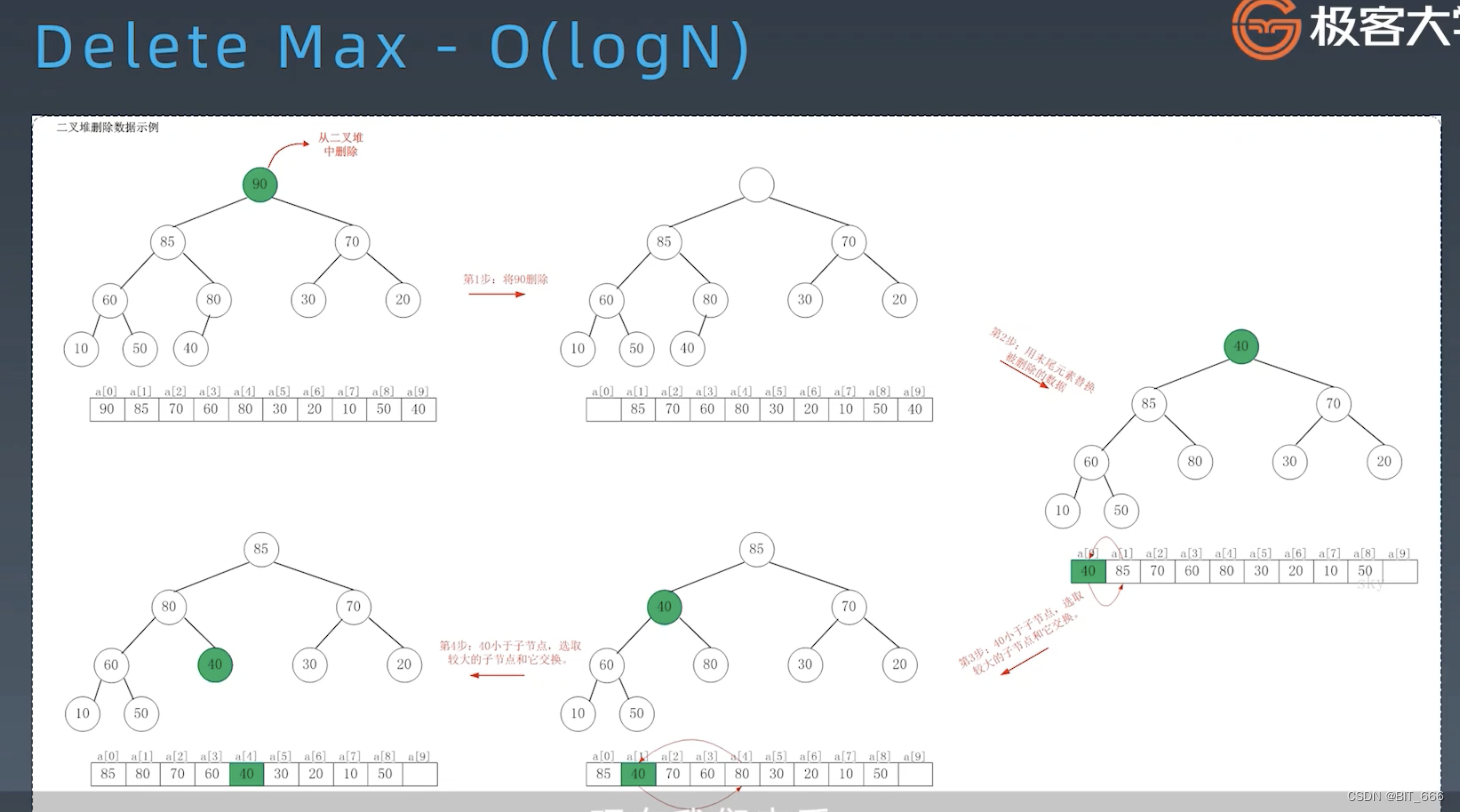
5.Heap 时间复杂度
再次重申下堆是一个抽象的结构,其有多种实现方式,就像是接口一样。这里最常见的实现方法为二叉堆,而随着实现方法的复杂,其 insert 和 delete 的复杂度也会更加友好。这里 Binaey Heap 的 find Min/Max 的时间复杂度为 o(1),其余时间复杂度为 o(logn)。
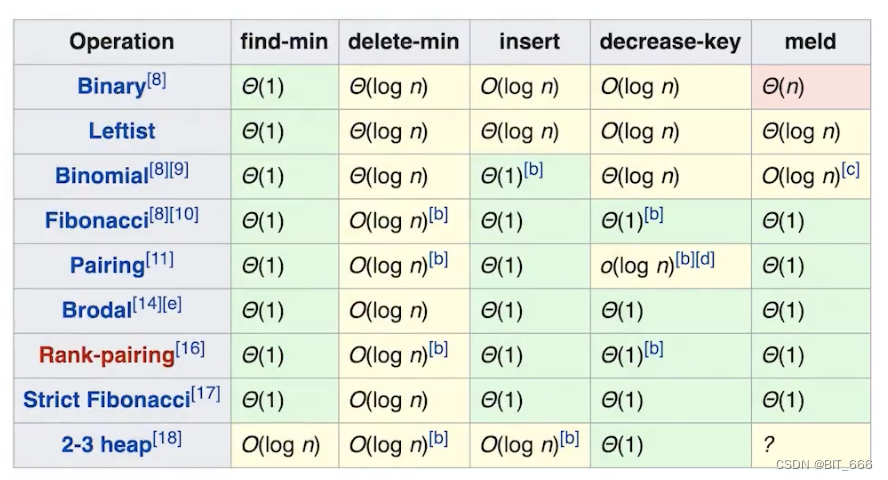
6.Insert & Delete 代码实现
◆ HeapifyUp

这里用了指针的方式,不断将较小的 Parent 节点与 Insert 节点互换,最终停止循环。
◆ HeapifyDown
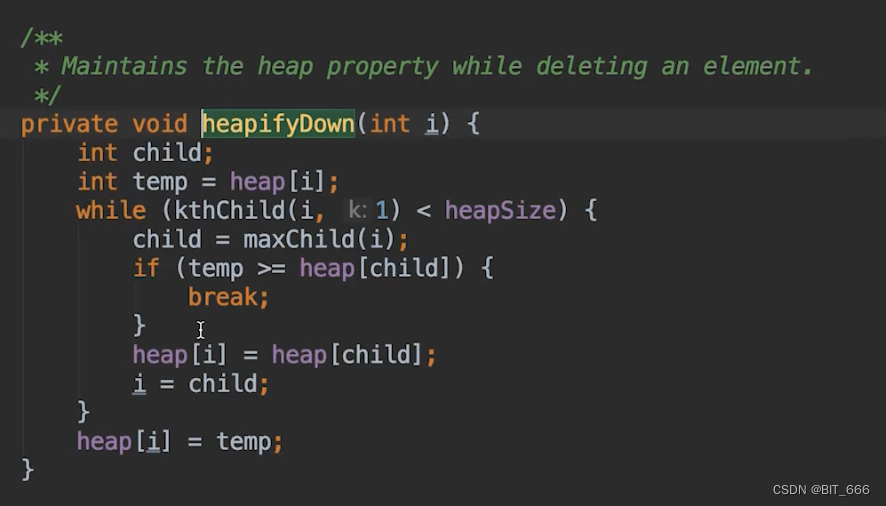
增加元素只需要与 Parent 节点比较,但是删除节点需要和左右子节点比较,所以需要使用 maxChild 函数寻找更大的节点进行交换,这样才能满足堆得性质。
三.经典算法实战
1.Smallest-K [M14]
最小的 K 个数: https://leetcode.cn/problems/smallest-k-lcci/

◆ 题目分析
既然是在堆的讲解下,所以我们可以直接使用 Heap,由于是最小的 k 个数,所以可以使用最小堆,每次返回堆顶元素并更新堆,执行 k 次即可。
◆ 小根堆
class Solution(object):def smallestK(self, arr, k):""":type arr: List[int]:type k: int:rtype: List[int]"""heapq.heapify(arr)res = []for i in range(k):res.append(heapq.heappop(arr))return respython 的 heapq 默认为最小堆,直接将元素通过 o(n) 复杂度构建一个 Heap,随后 pop k 次堆顶的元素即可。当然 heapq 提供 nsmallest 和 nlarggest (k, nums) 的函数可以直接获取前 k 个最小、最大的元素,其等价于 nums.sort()[:k]。
2.Sliding-Window-Max [239]
最大滑动窗口: https://leetcode.cn/problems/sliding-window-maximum/description/
◆ 题目分析
之前 ArrayList 部门我们通过 dequeue 双端队列实现了 k-window-max 的算法,一个技巧就是我们需要记录每个元素的索引,从而判断是否在窗口中。这里 python 默认的 heapq 为小根堆,通过 -1 * nums 转换为大根堆,随后遍历 k 窗口,取出堆顶最大值即可,注意在堆的维护过程中,排除索引 index 在 k-window 之外的元素。
◆ 大根堆
class Solution(object):def maxSlidingWindow(self, nums, k):n = len(nums)# 构造最大堆q = [(-nums[i], i) for i in range(k)]heapq.heapify(q)# 先获取前k个元素的 maxans = [-q[0][0]]for i in range(k, n):# 向堆添加新的元素heapq.heappush(q, (-nums[i], i))# 堆顶为窗口外元素则去除该元素while q[0][1] <= i - k:heapq.heappop(q)# pop 后仍然保持堆的结构,弹出堆顶最大值ans.append(-q[0][0])return ans对于最大、最小 k 个数的题目,我们都可以想到通过 heap 来实现,工程环境下直接使用对应的库即可。
3.Ugly-Number [264]
丑数: https://leetcode.cn/problems/ugly-number-ii/description/

◆ 题目分析
这个题目主要是理解比较困难,感觉是记忆性题目。1 是丑数,假设 x 是丑数,则 2x、3x、5x 也是丑数,所以我们依次加入堆中,第 n 次出队时,对应元素即为第 n 个丑数。
◆ 最小堆
#!/usr/bin/python
# -*- coding: UTF-8 -*-class Solution(object):def nthUglyNumber(self, n):""":type n: int:rtype: int"""nums = [2, 3, 5]# 去重appeared = {1}# 将初始化丑数放到队列里pq = [1]# 每次从队列取最小值,然后将对应数 2x 3x 5x 入队for i in range(1, n+1):x = heapq.heappop(pq)if i == n:return xfor num in nums:t = num * xif t not in appeared:appeared.add(t)heapq.heappush(pq, t)return -1
◆ 三指针
class Solution(object):def nthUglyNumber(self, n):if n < 0:return 0dp = [1] * n# 维护3个指针index2, index3, index5 = 0, 0, 0for i in range(1, n):# 每次看哪个位置乘出来的丑数最小dp[i] = min(2 * dp[index2], 3 * dp[index3], 5 * dp[index5])# 用过的索引 += 1if dp[i] == 2 * dp[index2]: index2 += 1if dp[i] == 3 * dp[index3]: index3 += 1if dp[i] == 5 * dp[index5]: index5 += 1return dp[n - 1]

4.Top-K-Freq-Ele [347]
前 k 个高频元素: https://leetcode.cn/problems/top-k-frequent-elements/description/

◆ 题目分析
这题找 k 个最大,还是使用堆即可,只不过需要预先做一次 word_count 统计词频,这里如果是 scala 可以直接用 tuple-2 再 sortBy(-_.2) 即可,python 的话就直接使用 heqpq.nlargest 即可。
◆ 最大堆 API
class Solution(object):def topKFrequent(self, nums, k):""":type nums: List[int]:type k: int:rtype: List[int]"""if k == 0:return []# 1.构造 word count 计数count = {}for i in nums:if i not in count:count[i] = 0count[i] += 1# 2.构造 Heapheap = [(val, key) for key, val in count.items()]# 3.取前 k 个元素return [item[1] for item in heapq.nlargest(k, heap)]这里使用 nlargest 获取前 k 个元素,但是我们构造时使用了全部数据,下面我们自己维护 k 个元素实现 heap。
◆ K-最大堆
class Solution(object):def topKFrequent(self, nums, k):""":type nums: List[int]:type k: int:rtype: List[int]"""if k == 0:return []# 1.构造 word count 计数count = {}for i in nums:if i not in count:count[i] = 0count[i] += 1# 2.构造 Heapre = []heapq.heapify(re)for key, val in count.items():# 添加元素heapq.heappush(re, (val, key))# 超过 k 就把堆顶最小的拿走,最后剩下 K 个最大的while len(re) > k:heapq.heappop(re)return [i[1] for i in re]
因为我们只维护了 k 大小的堆,遍历数组是 o(n),而堆内排序是 o(logk),所以时间快一些。
四.总结
本文结合上一篇文章的二叉树介绍了堆的概念以及常用的堆的功能应用,取前 k 个最大 or 最小的问题适合用堆实现,其次常用的二叉堆我们应该记住父子节点之间的关系。最后是常用堆的实现代码,这里我们都是调用 heapq 库,如果想要自己了解可以参考下述链接:
Heap Sort – Data Structures and Algorithms Tutorials




















