0 前言
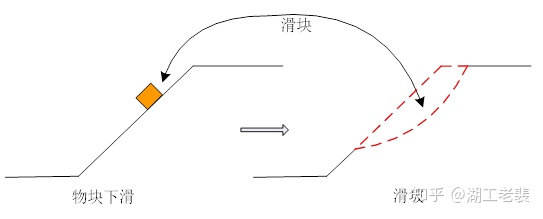
山体滑坡是常见的自然灾害,从理论分析的角度讲,滑坡的稳定性分析方法源自于高中物理学,如图1所示。前者的滑动分析非常简单,在已知滑块的重量以及接触面摩擦系数的基础上通过计算下滑力和抗滑力的关系即可分析其稳定性;对于后者,情况将变得非常复杂,第一个难题是不知道滑块的形状如何,第二个难题是土体材料能提供多大的抵抗力,同时还要考虑周围环境的影响,比如荷载、地下水等。
下面将结合Python介绍黏性土坡稳定性分析程序的实现过程,以最简单的瑞典条分法(Felenius法)为例,下面简要的介绍一下该方法,该方法有主要有如下一些假设:
- 1、对于第一个难题,其假设滑动面的形状为圆弧;
- 2、对于第二个难题,假设土坡滑动时滑动面上满足库伦准则;
- 3、刚体滑动、土体材料均质;
- 4、以滑动力矩和抗滑力矩的大小来判断土坡的稳定性。
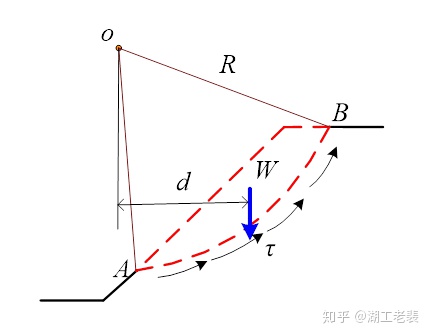
如图2所示,滑动力矩由滑块的重力产生,而抗滑力矩由土体材料在滑动面上的摩擦力提供。滑动力矩很容易求出,
而抗滑力矩为滑动面上的积分,
根据假定,破坏面上满足库伦准则,即破环面上的剪切力
定义安全系数 :
如果
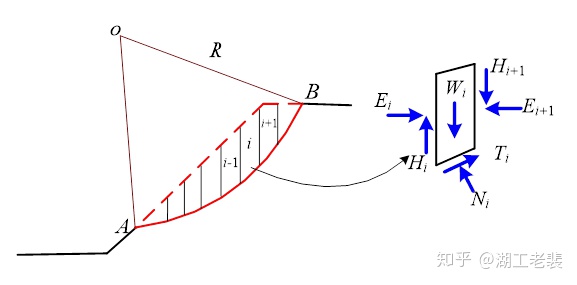
不难发现,滑块上的未知力、力作用点数量是大于每个条块的平衡方程数量,一般每个条块只有三个平衡方程,
水平方向的力平衡:
竖直方向的力平衡:
力矩平衡:
不过,作为最早的条分法,瑞典条分法不考虑条间力的平衡,
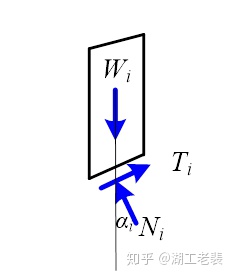
- 5、假定
作用点在底边中点,方向指向圆心,
指向底边中点,且滑动面上的法向合力
于是
。
最后化零为整,计算安全系数,
对于均质土体,
现在虽然知道了滑动面的形状以及计算安全系数的方法,但滑动面的位置并不清楚,如何找到滑动面的位置呢?最原始的方法是穷举,认为安全系数

可以看到,上面的穷举法是一个三重循环,需要预先给定圆心位置和半径的取值范围。
1 程序
瑞典条分法的理论并不复杂,编程难点是条块的划分,涉及到一些几何运算,如多线段与圆的交点,线段于线段的交点,四边形的面积运算等,这里采用Python的一个几何运算库Shapely实现这些几何运算。
本例程序需要用到的Python库包括数组运算库NumPy,几何运算库Shapely以及绘图库Matplotlib,使用pip安装,
pip 接下来开始编写程序,首先定义描述滑动面的类型Circle,由于Shapely中没有真正的圆类型,而是由多段线来描述,这也导致交点计算时速度会较慢,读者可以自行改进。下面所有的程序编写在同一个模块中,
from 然后定义土坡类型Slope,初始化参数为构成土坡轮廓线的点集,
class 接下来,定义根据滑动面信息条分滑块的方法cut(),其需要输入一个滑动面参数,本例为一个Circle对象,
def 在条块划分完成后,计算安全系数前需要设定土体的力学参数,定义set_soil_prop()方法,
def 然后计算安全系数,定义方法calc_fos(),
def 接下来,采用穷举法找到最小的安全系数,定义solve()方法,该方法需要传入一个参数search_box = [xmin,ymin,xmax,ymax],用于设置圆心的位置范围,
def 最后定义一个绘图方法,利用matplotlib库进行结果输出,默认输出最危险滑动面,
def 同时,clock_wise_points()函数定义如下,
def 2 算例
接下来用上述程序做简单的算例,
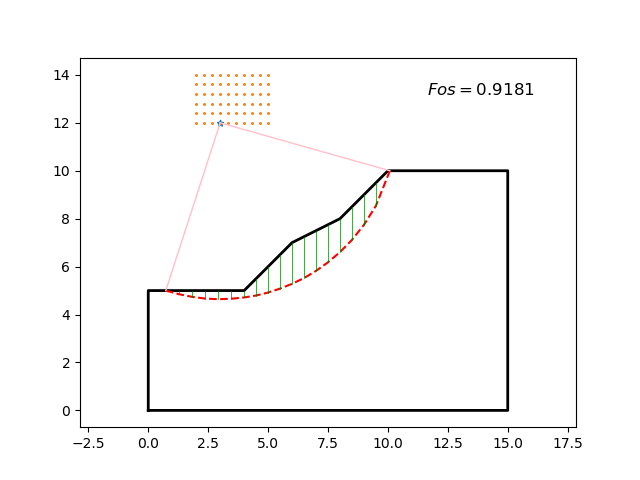
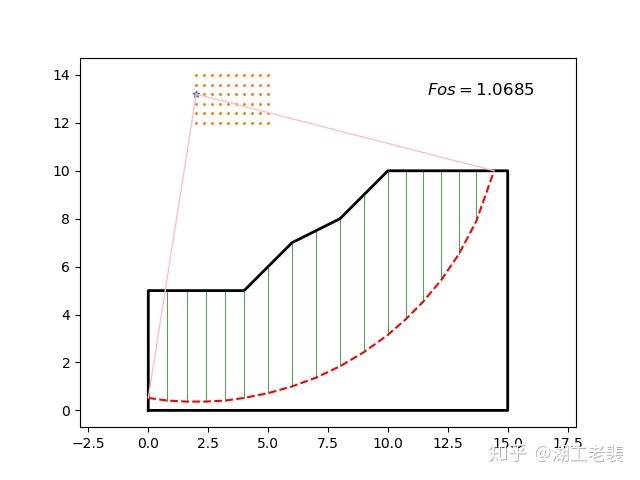
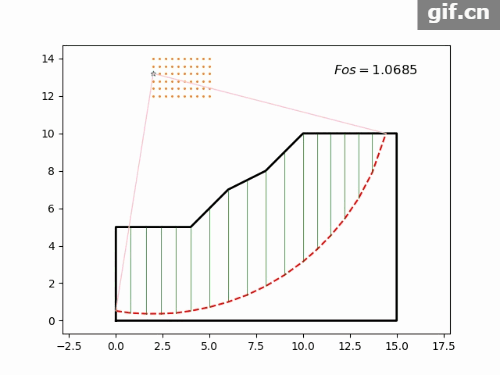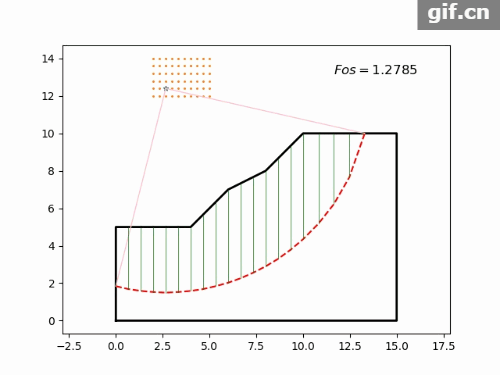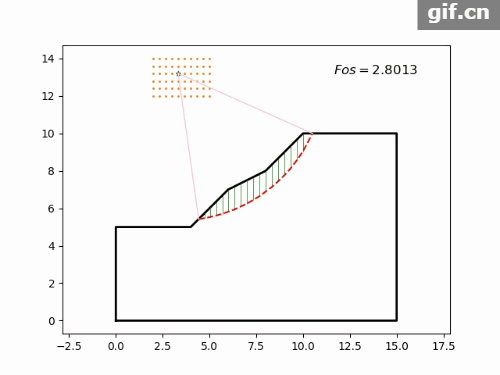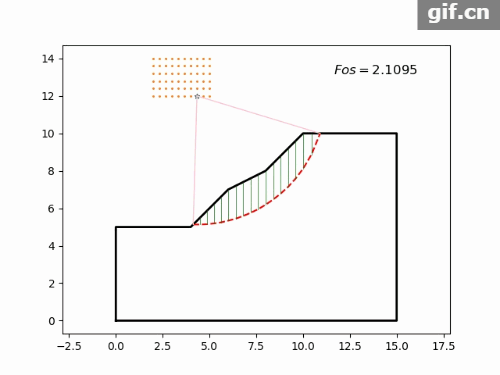
if 计算结果如图5所示,动态搜索见图6。
修改土体参数,比如增大内摩擦角,结果如图7所示。
s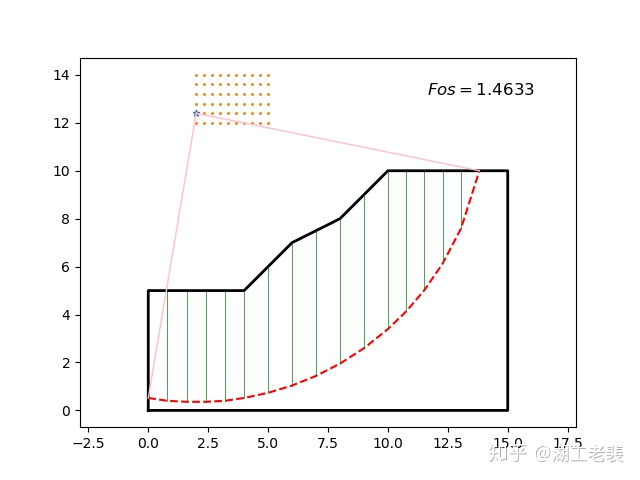
修改圆心边界,结果如图8所示。
s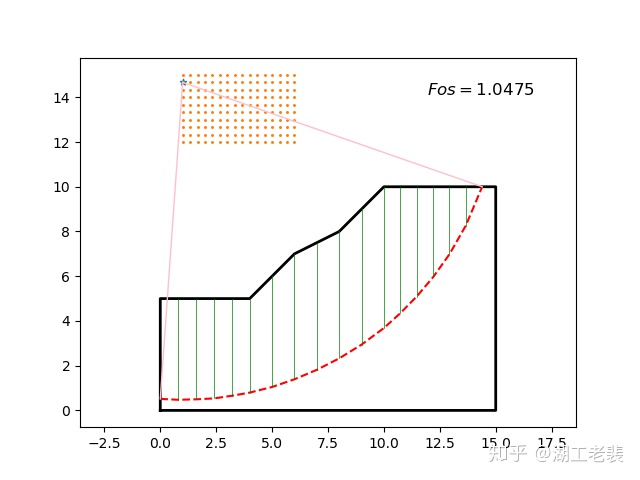
可以看到,不光是修改土体的力学参数,修改圆心的位置也会影响计算结果。
3 总结
根据上文了解到,一直以来,黏性土坡的稳定性分析理论的研究思路主要集中在以下几个方面,
- 滑动面形状研究,目前主要分为圆弧滑动面和任意形状滑动面;
- 条块力学平衡假设研究,通过设定假设条件,增加方程数数量或减少未知数的数量来满足条块的平衡;
- 最危险滑动面搜索方法研究,穷举法不仅效率低,而且由于步长的存在,也只是近似解,所以考虑将最优化理论应用于搜索最危险滑动面。
4 说明
- 由于水平有限,笔者无法保证程序在极端几何条件下运行不会出现bug;
- 本例仅介绍瑞典条分法的基本程序实现,抛砖引玉,未考虑的因素包括地下水影响、荷载作用,多土层分布的情形,后期考虑加入这些功能,也可能会实现更多的条分法,比如常用的Bishop法、Janbu法、Spence法等,欢迎各位同仁交流和指正。



















