中公教师通过对全国教师资格考试考情的分析，总结出全国教师资格考试《信息技术学科知识与能力》算法与程序设计部分的知识点，并提供了该模块的相关考试试题，希望能帮助考生抓住考点、有针对性地复习。

一、算法与程序设计模块考点分析

通过对全国统考教师资格《信息技术》初中、高中试卷分析得出：算法与程序设计部分主要的考点是算法流程图和结构化程序设计的三种基本结构。

二、算法与程序设计模块习题及解析

1.某计算公式的流程图如图1所示，输出结果s的值为( )。

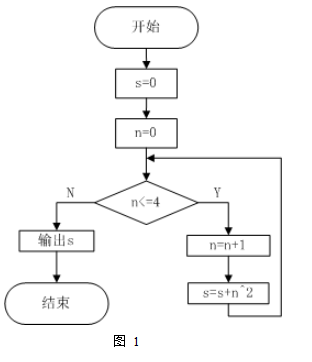
A.14 B.30 C.55 D.91

1..【答案】C。解析：判断框n<=4;当判断框中n=4时，右边n=4+1=5，S=0+1^2+2^2+3^2+4^2+5^2=55;n=5不满足判断框中的条件，所以流程图转向左边，输出S的数值为55。正确答案为C。

2.计算s=1+1/3+1/7+1/15+……的流程图如图2所示，若要计算前5项的和，①处应该输入的判断条件是( )。

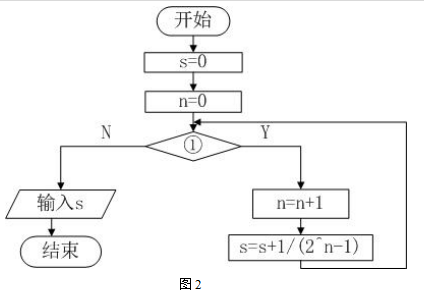
A.n<6 B.n<=5 C.n<4 D.n<=4

2.【答案】D。解析：题干当中求的是前5项的和，那么n的取值是从0开始的，因此当等于4的时候，已经满足题干中“5”的要求，因此选项D正确。

3.计算S=1+3+5+7+9的算法流程如图3所示，若要计算S=1×3×5×7×9，则下面流程图中的S=S+X与X=X+2应该改为( )。

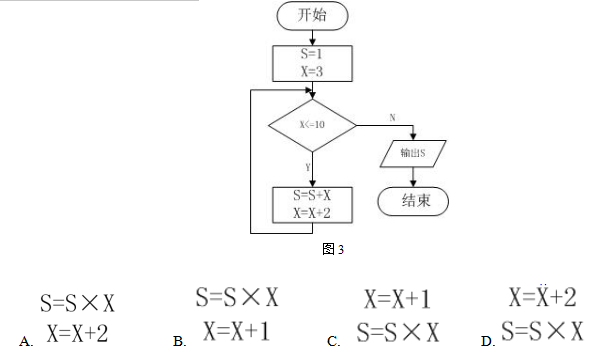
3.【答案】A。解析：题中将S=1+3+5+7+9，改成计算S=1×3×5×7×9，变量x的步长还是2，x=x+2，s是求累积s=s×x，答案选A。

4.某算法流程如图4所示，当变量sum的初始值为5，提供输入变量i的值为12时，则变量sum的输出值为( )。

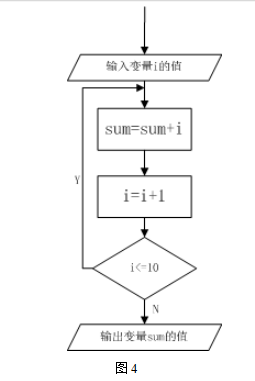
A.5 B.6 C.17 D.29

4.【答案】C。解析：变量sum初始值为5，变量i的值为12，输入算法开始计算，sum=sum+i，i=i+1，得出sum=17，i=13，i>10不符合条件，所以输出sum的值为17。

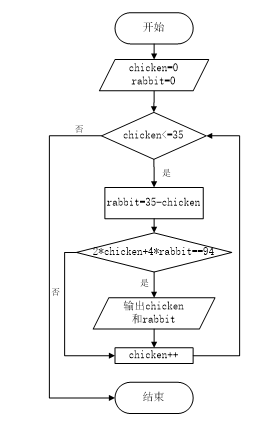
5.请画出利用穷举法解决鸡兔同笼问题的流程图。

鸡兔同笼问题：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何?

5.【参考答案】

三、考点分析

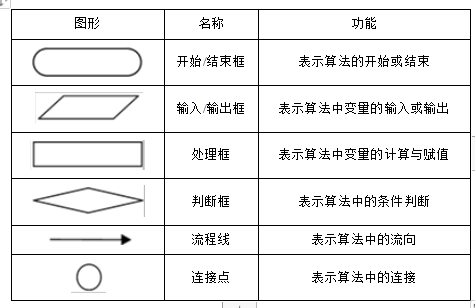
考点一：流程图

流程图是由一些图框和流程线组成的，其中图框表示各种操作的类型，图框中的文字和符号表示操作的内容，流程线表示操作的先后次序。也称为程序框图，它是算法的一种图形化表示方法。

优点：形象、直观、容易理解。

考点二：结构化程序设计三种基本结构

1.顺序结构程序设计

顺序结构是最简单的程序结构，也是最常用的程序结构，只要按照解决问题的顺序写出相应的语句就行，它的执行顺序是自上而下，依次执行。

例如，a=3，b=5，现交换a，b的值，这个问题就好像交换两个杯子水，这当然要用到第三个杯子，假如第三个杯子是c，那么正确的程序为：c=a;a=b;b=c;执行结果是a=5，b=c=3。

2.选择结构程序设计

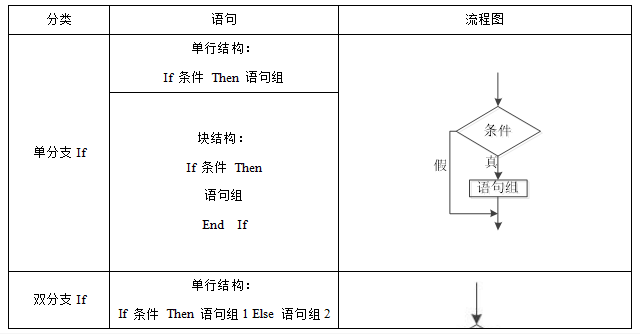
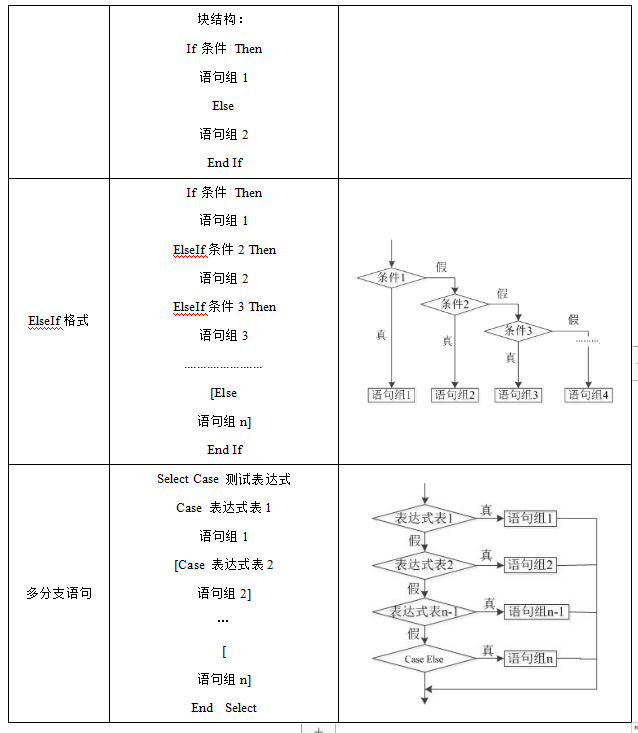
3.循环结构程序设计

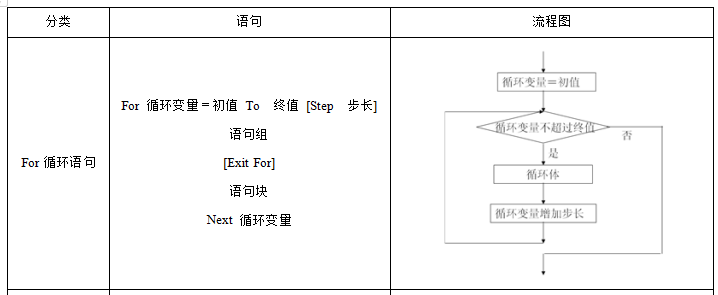
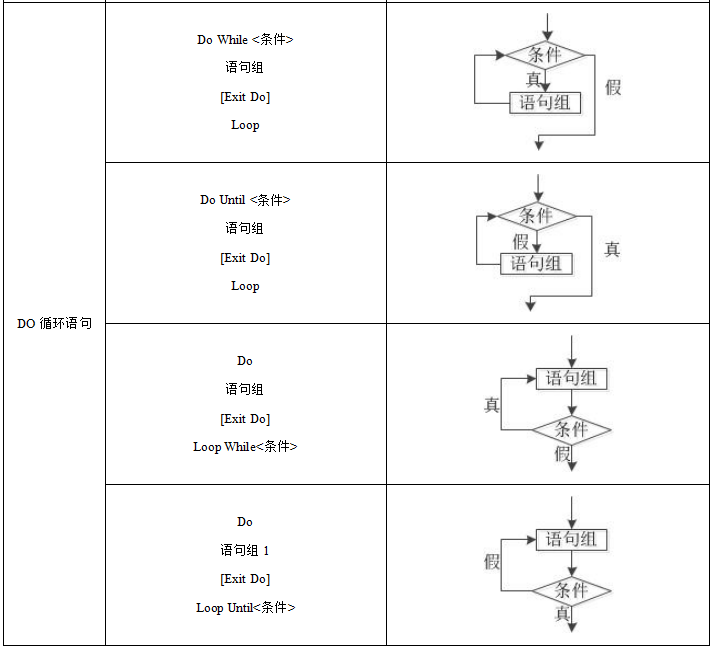
考点三：算法设计的基本方法

1.解析法

解析法是指用解析的方法找出表示问题的前提条件与结果之间关系的数学表达式，并通过表达式的计算来实现问题求解。用解析法解决问题的关键就是找到求解问题的解析表达式。

实例：出租车计费问题。起步价10元(三公里内)，3~10公里之间每公里2.1元，超出10公里部分每公里3元。通过分析可以得出车费与行车距离的数学表达式，然后根据表达式进行求解。

2.穷举算法

穷举法也叫枚举法或列举法。在已知答案范围的情况下，依次地枚举该范围内所有的取值，并对每个取值进行考查，确定是否满足条件。经过循环遍历之后，筛选出符合要求的结果。

实例：百钱买百鸡问题。根据钱的总数和鸡的总数可以得到三个未知数、两个方程组。由数学思想可以，三个未知数需要三个方程组进行求解。为了解答该问题，可以固定其中一个未知数的值，求解其他两个未知数，直至枚举出所有的可能解。

3.递归法

递归算法的特点：

(1)存在某个特定条件，在此条件下，可得到指定的解，即递归在终止状态。

(2)对任意给定的条件，有明确的定义规则，可以产生新的状态并将最终导出终止状态，即存在导致问题求解的递归步骤。

实例：求n!问题。n>0时，n!=n*(n-1)!;n=0时，n!=1。

在递归调用中需用同一变量名n，但值不同，所以在调用前必须先把n的原值保存，再赋以新值，然后进入调用。调用结束后，再把保存的值取出，使n恢复原来的值。包含有递归调用的算法，就叫做递归算法。

4.递推法

递推是迭代算法中一种用若干步可重复的简单运算来描述复杂数学问题的方法。采用递推的方法来求解的话，第n项之前的每一项都必须计算出来，最后才能得到所需要的第n项的值。

实例：猴子吃桃问题。每天吃掉当天的一半多一个，第七天剩一个，问第一天有多少桃。需要根据第7天的个数求第6天的个数，直至第一天。