在本系列分享中我们将介绍BladeDISC在动态shape语义下做性能优化的一些实践和思考。本次分享的是我们最近开展的有关shape constraint IR的工作，鉴于篇幅较长，为了提升阅读体验，我们将分享拆分为两个部分：

• Part I 中我们将介绍问题的背景，面临的主要挑战和以及我们做shape constraint IR的动机；
• Part II 中我们将介绍shape constraint IR的设计，实现以及一些初步的实验结果；

本篇是关于Part I的介绍，Part II的介绍将后续发出。

背景和挑战

主流的AI模型在部署时一般都具备不同程度的动态shape问题，比如输入图片尺寸，batch size 或者序列长度的变化等。与静态shape语义下做优化相比，在动态shape语义下做优化由于缺少具体的shape信息往往具有更大的难度，主要体现在以下几个方面：

挑战1：优化目标的转变。在静态shape下，我们的优化目标是希望在给定的shape下，尽可能逼近理论上限的速度，针对不同的shape可以使用不同的优化手段，而在动态shape语义下，我们优化目标是希望使用一套方法提升在整个shape分布上的平均性能，更强调的是优化方法的跨shape可迁移性和稳定性。因此很多在静态shape下常用的优化，比如profling驱动的策略，将不再简单可用。

挑战2：更少的有效信息。优化AI模型时很多常见的手段都把一些shape关系的断言是否成立作为优化触发的前置条件。比如在计算图化简时消除冗余的broadcast op，需要依赖于判断输入和输出是否具有相同的shape。在静态shape语义下，判断常量shape是否相等是显然的，而动态shape语义下，判断symbolic shape相等则困难的多，而一旦我们无法有效判断这些前置的shape关系断言是否成立，后续优化都无法进行，因而丢失很多优化机会，拉大与静态shape情况下性能的差异。

挑战3：更复杂的计算图。在动态shape语义下，由于shape不再是编译（或者优化）期间的常量，整个计算图中混杂着计算shape的IR以及计算data的IR，使得整个计算图的分析和优化都变得更复杂，同时也会引入更多shape相关计算的开销。

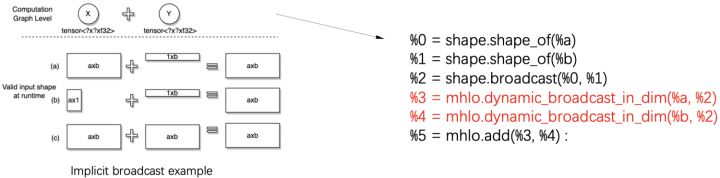
下图中展示了一个支持numpy语义implicit broadcast (IB)的Add OP的例子以说明计算图变复杂的具体过程。在IB语义下，Add OP在运行时会根据输入shape之间的关系，隐式的插入broadcast运算，所以下图左侧中展示的三种可能输入都是合法的。在静态shape语义下我们很容易在编译期就区分开实际是那种情况，故而在编译时只需要对一种具体情况进行处理，而在动态shape语义下，由于编译期间无法进行区分，我们需要确保编译的结果在三种情况下都可以工作，因而会在计算图中引入显示的shape 计算的IR以及broadcast操作（如下图右侧所示）。在这个例子中上层框架中一个普通的Add OP在动态shape语义下，也会被展开成一个复杂的子图。

也正因为上述的这些挑战，目前成熟的优化工具（如TensorRT，XLA/TVM）对于动态shape支持都还比较有限。BladeDISC是阿里云计算平台PAI团队自研的一款原生支持动态shape的AI编译器。在过往一段时间我们开发BladeDISC优化动态shape模型的过程中，我们发现尽管不知道shape的具体的数值，但是通过充分发掘和利用Tensor的shape之间的结构化关系或者Tensor shape自身的分布特点，可以有效的解决上述挑战。在这里我们把Tensor的shape之间的结构化关系或者Tensor shape自身的分布统称为shape constraint。更进一步的，我们发现通过将shape constraint作为第一等公民引入到IR中，可以最大化的发挥shape constraint的效能。本文中我们将介绍BladeDISC中shape constraint IR的定义以及如何利用它来辅助完成一系列动态shape语意下的优化以解决上述挑战，缩小与静态shape之间的性能差异。

动机

为什么选择shape constraint？

在上一章节中我们分析了在动态shape语义下给做优化所带来的一系列挑战。我们发现使用shape constraint可以有效的解决这些优化上面临的困难。以下我们将分别介绍使用shape constraint如何有效解决上述的三个挑战。

应对挑战1：跨shape可迁移性

在具体分析之前，我们先看shape constraint在本文中的定义。假设一个tensor的rank是N，则该tensor的shape可以记为(d0, d1, ... dN-1)，其中di表示的是该tensor在第i个轴上所具有的大小，也记为第i个轴的dimension size。文本中讨论的shape constraint可以分为以下两类：

• shape结构化约束。该类约束描述的是dimension size之间的相关关系，比如：
  • dimension size相等关系：某一个tensor的di与另外一个tensor的dj具有相同的大小，或者同一个tensor的di与dj具有相同的大小；
  • tensor元素个数相等：即一个tensor和另外一个tensor具有相同数量的元素；
  • dimension size乘积相等关系：比如reshape（[a, b, c, d]） -> [a*b, c*d]
• shape分布约束。该类约束描述的是某个或某几个dimension size的（联合）分布，比如：
  • di % 4 = 0，di != 0, di * dj=10;
  • likely values: 即描述某个dimension size更大概率可能取到的值；
  • value range：即描述某个dimension size可能的取值区间；

由上述定义本身我们可以立刻得到一个结论：由于无论是shape结构化约束还是分布约束都不依赖于具体的shape值，因此基于shape constraint而构建的优化策略天然具备跨shape可迁移性。

应对挑战2：shape关系断言分析

很多重要的优化都将一些shape关系的断言是否成立作为优化触发的前置条件，比如：

• 计算图化简。比如上文提到的消除冗余的broadcast节点的例子。
• 计算图layout全局优化。计算密集型算子的性能和其输入输出的数据排布（layout）有很强的关系，一个更合适的layout往往具有更好的性能。而一般最优的layout是随着shape而变化的，导致在动态shape语意下无法静态确定最优的layout；这里一种优化策略是：将shape兼容的计算密集算子分到一组，只需要在组间插入layout转化的算子，而组内由于可以确认使用同一种layout而不必再插入layout转化的算子，从而提升性能；这里shape兼容的断言是优化触发的前置条件。
• fusion决策。在做算子融合时并不是越多越好，只有将shape兼容的算子进行融合才会取得比较好的效果，同样里shape兼容的断言的判定是做算子融合的前置条件。

在动态shape语义下，由于不知道shape具体的值，symbolic shape关系的断言的分析往往是困难的。symbolic shape关系的断言可以看成是symbolic dimension size间的关系断言的逻辑关系表达式，因而问题可以转换成对于symbolic dimension size间的关系断言的判定。而由前述shape constraint定义可知，symbolic dimension size间的关系断言本身是shape constraint一个实例。在这里我们把判定symbolic dimension size间的关系断言是否成立的这个问题转换成该断言是否是已知原子shape constraint的组合。这里“原子”的定义是不能够通过其他shape constraint 的实例的组合得到。举个例子，假设我们需要判定tensor A: tensor是否比tensor B: tensor具有更多的元素个数，这个问题经过转换过之后可以变成dimension size关系a > b是否成立。

在完成上述问题的转换之后，目前剩下的未解决的问题是：如何获得已知结果的原子shape constraint。具体来说有以下几种方式：

• 由用户提供或在JIT编译期间自动捕获。比如用户可以提供关于模型输入shape range，JIT编译期间可以将捕获到的一组输入shape当作likely value 注入编译流程等。
• 由op定义所携带的shape consraint信息。比如：
  • elementwise op的输入和输出应该具有相同的大小；
  • mhlo.dynamic_reshape op的输入和输出应该具有相同的元素个数；
  • mhlo.concatenate op 的输入和输出在非拼接的轴上应该具有相同的大小；
• 分析shape计算的IR或者通过传播已有的shape constraint来获得新的信息，比如：

在充分利用上述来源原子shape contraint的基础上，我们可以大幅减少由于shape未知导致一些优化前置条件无法判断，进而导致优化无法生效的问题。

应对挑战3：shape计算开销及更复杂的计算图

在动态shape语义下，会引入更多的shape计算的开销，整个计算图会变得更复杂。

对于shape计算开销，shape结构化约束我们可以抵消大量重复的symbolic计算，从而尽可能减小额外的开销。

对于计算图化简而言，我们一方面可以通过利用shape结构化约束消除一部分的冗余计算，比如前文中提到的由于IB问题引入的大量broadcast op可以在计算图化简中消除。剩下的无法利用shape结构化约束消除的broadcast可以进一步利用以下shape分布约束进行优化：IB触发（即需要插入隐式的broadcast）的概率远小于IB不触发的概率。通过生成带IB和不带IB两个版本的（如下图所示），让common case变得更快，从而提升期望性能；

为什么需要shape constraint IR？

shape constraint在动态shape语义下很有用，但是要用好它却并不容易。由于在整个pass pipeline中都可能会使用到shape constraint信息，因此我们需要一种方式将shape constraint信息在不同的pass之间进行传递。BladeDISC早期时使用是一种隐式传递的策略，即每个pass在需要使用shape constraint信息时会通过分析一遍IR来重建shape constraint信息。不难看出在上述的方案中shape constraint本身并不是IR一部分，这种策略带来的问题是：

• 通过分析IR的方式一般只能够重建（部分）结构化约束信息，大部分的分布约束信息无法通过直接分析data计算IR来重建，而分布约束对于动态shape语义下的性能优化同样很重要；
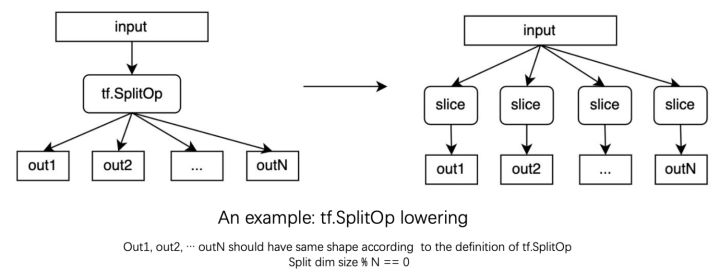
• 在整个pass pipeline中IR会经历多次的lowering （如TF/Torch dialect -> mhlo -> lmhlo -> ...），在每次lowering的过程中都可能会丢失一部分shape constraint信息，比如下图中所展示的tf.SplitOp的例子。在这个例子中上层的tf.SplitOp会被lower成一系列的mhlo的SliceOp。根据tf.SplitOp的定义我们可以知道它的所有输出（假设有N个）应该具有相同的shape，且输入在被拆分的轴上的dimension size可以被N整除，这些信息在我们lower到mhlo时如果只进行data computation的转换，而不进行shape constraint信息的转换，将会被丢失，从而使得后续的pass无法再利用相应的信息进行优化；

为了解决上述的问题，我们更进一步将shape constraint 作为第一等公民引入到IR中，使得可以对结构化约束信息和分布约束信息进行统一的建模，同时也确保在整个pass pipeline中各个pass可以看到一致的shape constraint信息，进而更好的支持在不同的阶段完成各自适合的优化。

原文链接

本文为阿里云原创内容，未经允许不得转载。