向量空间模型VSM及余弦计算
向量空间模型的基本思想是把文档简化为以特征项(关键词)的权重为分量的N维向量表示。
这个模型假设词与词间不相关(这个前提造成这个模型无法进行语义相关的判断,向量空间模型的缺点在于关键词之间的线性无关的假说前提),用向量来表示文本,从而简化了文本中的关键词之间的复杂关系,文档用十分简单的向量表示,使得模型具备了可计算性。
在向量空间模型中,文本泛指各种机器可读的记录。
用D(Document)表示文本,特征项(Term,用t表示)指出现在文档D中且能够代表该文档内容的基本语言单位,主要是由词或者短语构成,文本可以用特征项集表示为D(T1,T2,…,Tn),其中Tk是特征项,要求满足1<=k<=N。
下面是向量空间模型(特指权值向量空间)的解释。
假设一篇文档中有a、b、c、d四个特征项,那么这篇文档就可以表示为
D(a,b,c,d)
对于其它要与之比较的文本,也将遵从这个特征项顺序。对含有n个特征项的文本而言,通常会给每个特征项赋予一定的权重表示其重要程度,即
D=D(T1,W1;T2,W2;…,Tn,Wn)
简记为
D=D(W1,W2,…,Wn)
我们把它叫做文本D的权值向量表示,其中Wk是Tk的权重,1<=k<=N。
在上面那个例子中,假设a、b、c、d的权重分别为30,20,20,10,那么该文本的向量表示为
D(30,20,20,10)
在向量空间模型中,两个文本D1和D2之间的内容相关度Sim(D1,D2)常用向量之间夹角的余弦值表示,公式为:
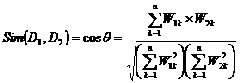
其中,W1k、W2k分别表示文本D1和D2第K个特征项的权值,1<=k<=N。
下面是利用模型进行余弦计算的示例。
在自动归类中,我们可以利用类似的方法来计算待归类文档和某类目的相关度。
假设文本D1的特征项为a,b,c,d,权值分别为30,20,20,10,类目C1的特征项为a,c,d,e,权值分别为40,30,20,10,则D1的向量表示为
D1(30,20,20,10,0)
C1的向量表示为
C1(40,0,30,20,10)
则根据上式计算出来的文本D1与类目C1相关度是0.86。
那么0.86具体是怎么推导出来的呢?
在数学当中,n维向量是
V{v1,v2,v3,...,vn}
模为
|v|=sqrt(v1*v1+v2*v2+…+vn*vn)
两个向量的点积
m*n=n1*m1+n2*m2+......+nn*mn
相似度
sim=(m*n)/(|m|*|n|)
它的物理意义就是两个向量的空间夹角的余弦数值。
下面是代入公式的过程:
d1*c1=30*40+20*0+20*30+10*20+0*10=2000
|d1|=sqrt(30*30+20*20+20*20+10*10+0*0)=sqrt(1800)
|c1|=sqrt(40*40+0*0+30*30+20*20+10*10)=sqrt(3000)
sim=d1*c1/(|d1|*|c1|)=2000/sqrt(1800*3000)=0.86066
完毕。
)


















