前言:花了一个半月时间学习了 北大丘维声的《高等代数》、北理史荣昌的《矩阵分析》、清华张贤达的《矩阵分析与应用》;北大与哈工大的网课。
本质:(万物皆矩阵)矩阵论主要研究矩阵,对于图像、神经网络等可表示成矩阵形式,然后结果矩阵的处理方法,对其进行操作,例如分解,基本运算等。
一、矩阵(矩阵表示单个事物)
1.1矩阵的基本运算
基本运算:加法;数乘;矩阵乘法;转置;內积;外积
拓展运算:直和;Hadamard积(Schur积);Kronecker积(直积);Khatri-Rao积(对应列Kronecker积)
注:向量之间的外积可由Kronecker积表示;Khatri-Rao积由两个列数相同的矩阵 对应列Kronecker积构成
矩阵结构运算:向量化(列向量化vec(A),行向量化revec(A)),矩阵化(分行向量矩阵化与列向量矩阵化)
1.2矩阵的性能指标
(实对称矩阵或Hermite矩阵)二次型:
(方阵)行列式:刻画矩阵的奇异性;等于特征值之积
(方阵)特征值:1、刻画矩阵的奇异性(是否存在0特征值) 2、刻画矩阵的正定性 3、刻画对角元素之和
注:上,下三角矩阵的特征值等于主对角元素;实对称矩阵不同特征值对应的特征向量是正交的。
(方阵)迹:等于特征值之和
秩:刻画矩阵的奇异性,行秩等于列秩(对于张量不一定成立)
奇异值:
1.3矩阵的度量(内积与范数)
向量:(常采用典范內积
注:L2范数常称Euclidean范数或者Frobenius范数
矩阵:
矩阵內积:
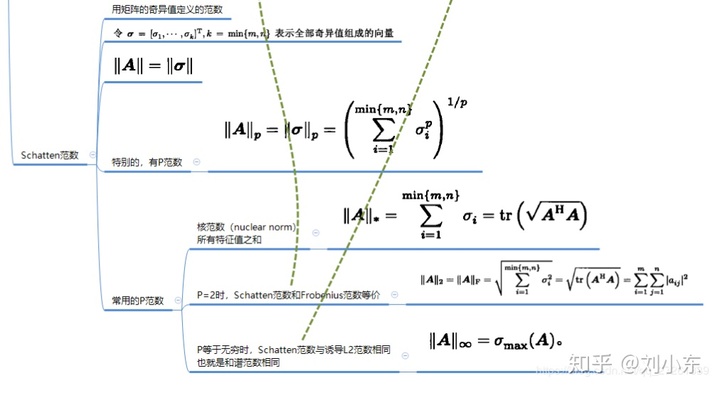
矩阵范数:诱导范数、元素形式范数、Schatten范数
(1)诱导范数定义:
注:常用的诱导范数为p-范数
(2)“元素形式”范数:
注:当p=2时的范数称为L2范数,Euclidean范数,Frobenius范数
(3)Schatten范数(用矩阵奇异值定义的范数)
1.4 逆矩阵
(1)正方满秩矩阵的逆矩阵
(2)非正方满(行或列)秩的伪逆矩阵
左逆矩阵
右逆矩阵
注:左伪逆矩阵与超定方程的最小二乘解有关,右伪逆矩阵与欠定方程的最小二乘解有关
(3)非正方秩亏损的伪逆矩阵(Moore-Penrose逆矩阵,广义逆矩阵)
满足以下4个条件的矩阵,称为Moore-Penrose逆矩阵
1.5 特殊矩阵
(1)(方阵)实对称矩阵与复共轭对称矩阵(Hermite矩阵)
(2)(方阵)实正交矩阵与酉矩阵(复数域)
注:酉矩阵的列或者行向量皆为标准正交基;酉矩阵对应的酉变换保內积,保长度
(3)(方阵)正规矩阵
注:对称矩阵hermite矩阵,正交矩阵,酉矩阵皆为正规矩阵。
(4)置换矩阵:每一行每一列有且仅有一个非零元素1。(等于初等矩阵的乘积,左乘A表示行变换,右乘A表示列变换,)
注:置换矩阵的三种特殊情况:交换矩阵,互换矩阵,位移矩阵
(5)带型矩阵(三角矩阵为带型矩阵的特例)除主对角线上下几条斜线以外元素皆为0
(6)求和向量与中心化矩阵(数理统计中常用)
求和向量(元素全为1):n个标量的求和可表示为求和向量与另一向量的內积
中心化矩阵:
注:
Cnx向量內积等于C的二次型,等于样本数据的协方差
(7)Vandermonde矩阵,Fourier矩阵,Hadmard矩阵(信号处理中常用)
1.6 常数、函数、随机矩阵
注:矩阵元素可为常数、函数、随机变量
函数矩阵的极限、导数、积分等于对应元素求极限、导数、积分;其余与常数矩阵类似
1.7 矩阵函数
(1)利用矩阵幂级数定义矩阵函数(北理数用解析定义)

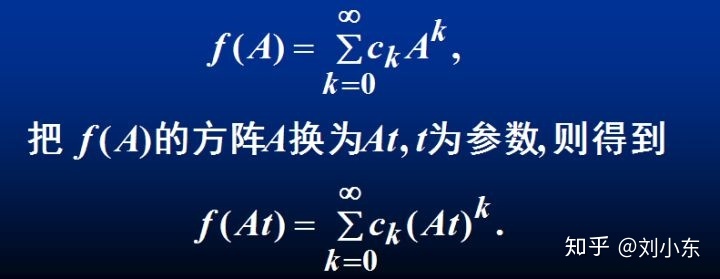
(2)常见矩阵函数(类似利用一元多项式环的通用性质直接得到,与常见函数的泰勒展开式一致)

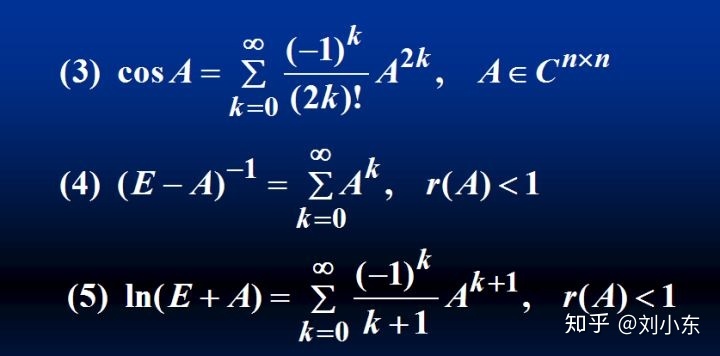
(3)矩阵函数值的计算









由该定理,我们可以实现降次的目的。
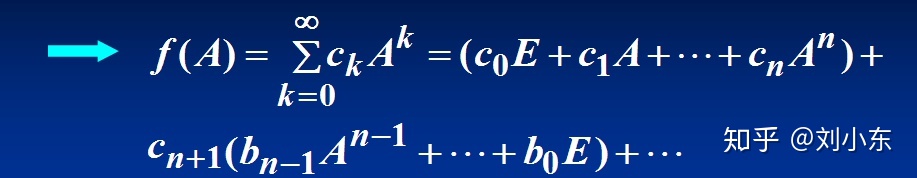
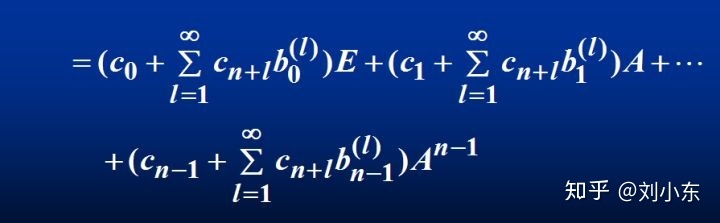

(4)矩阵函数微分(其中矩阵函数值根据f(X)中f的不同,最终结果可为标量、向量、矩阵)(梯度矩阵与Hessian矩阵最优化问题中常用)
1、以实矩阵为变元的实函数(梯度矩阵等于Jacobian矩阵的转置)
注1:Jacobian矩阵为按行向量形式定义的偏导矩阵,梯度矩阵(最优化问题中常见)为按列向量形式定义的偏导矩阵;Jacobian矩阵也有称协(同)梯度矩阵
注2:一阶实矩阵微分是辨识实矩阵函数的梯度矩阵、Jacobian矩阵的有效数学工具;(即可通过对矩阵函数求一阶微分的结果中直接得到梯度矩阵与Jacobian矩阵,具体表示式见张贤达书第三章)
注3:二阶实矩阵微分是辨识实矩阵函数的Hessian矩阵(二阶偏导矩阵)的有效数学工具;(即可通过对矩阵函数求二阶微分的结果中直接得到实函数的Hessian矩阵,具体表示式见张贤达书第三章)
2、以复矩阵为变元的实函数(梯度矩阵等于Jacobian矩阵的转置,会得到梯度&共轭梯度)注:一阶复矩阵微分可以标识梯度矩阵与共轭梯度矩阵,Jacobian矩阵与共轭Jacobian矩阵;二阶复矩阵微分可以标识复Hessian矩阵
二、代数系统(矩阵表示两系统之间的关系)
2.1 代数系统(线性空间、环、域)
线性空间:定义了加法与数乘,满足8条
环:定义了加法与乘法,满足6条,乘法需要满足结合律与左右分配律
注:乘法满足交换律的环称为交换环,乘法中含有单位元的环称为有单位元的环
举例:一元多项式环,n元多项式环,整数集
域:含有单位元的交换环,并且其中每个非零元都是可逆元
举例:数域
2.2 线性映射(描述两个线性空间的映射问题)
1、线性映射的矩阵表达式
线性变换矩阵:
线性映射矩阵:
注:已知向量a在
2、线性变换的Jordan标准型(方阵,矩阵相似的“最简形式”)

证明思路:基于不变子空间可将矩阵块三角化与块对角化,即P1与P2皆为方阵的不变子空间,则实现矩阵的块对角化。若引入一维不变子空间,即特征向量作为P的列向量,当存在n个线性无关的特征向量(表示满足P可逆),则实现矩阵的对角化。

最终得到最重要的Jordan标准性:

3、特殊的线性变换
注:一个方阵对应与一个线性变换,具有特殊性质的矩阵对应的线性变换,同样具有某些特性
(1)酉变换、正交变换(保内积,保长度),属于保距同构映射
注:酉矩阵一定酉相似于对角矩阵,其主对角元素为模为1的复数(因为酉矩阵特征值的模等于1);正交变换正交相似于分块对角矩阵
(2)Hermite变换、对称变换
注:实对称矩阵一定能正交相似于对角矩阵,n级Hermite矩阵一定能酉相似于对角矩阵
(3)正交投影
注:若P即为幂等矩阵又为Hermite矩阵,即可作为一投影算子。I-P则为正交投影算子(往垂线方向投影)
2.3 具有度量的线性空间(內积空间、赋范空间、Hilbert空间)
內积空间:只要规定了一个內积(正定的对称双线性函数)的线性空间皆可称为內积空间
注1:有限维实內积空间称为欧几里得空间,简称欧式空间;有限维复內积空间称为酉空间,
注2:(正定性二者皆满足)复內积与实內积的区别:1、复內积满足共轭对称性,实內积满足对称性;2、实內积对两个变量都是线性的,复內积对于一个变量线性,对另一个共轭线性
赋范空间:定义了范数的空间,可度量向量长度、距离、领域
注:定义了L2范数的赋范空间称为Eculidean空间
完备赋范空间:(完备性)
1、Banach空间:每一个Cauchy序列极限都存在于空间中
2、Hibert空间:每一个Cauchy序列的范数的极限都存在于空间中
3、一个有限维的赋范空间一定是Banach空间,自动满足Cauchy序列极限收敛的条件





微机原理期终考试试题(B卷)...)









:安装mysql 5.7)



