2023.7.19

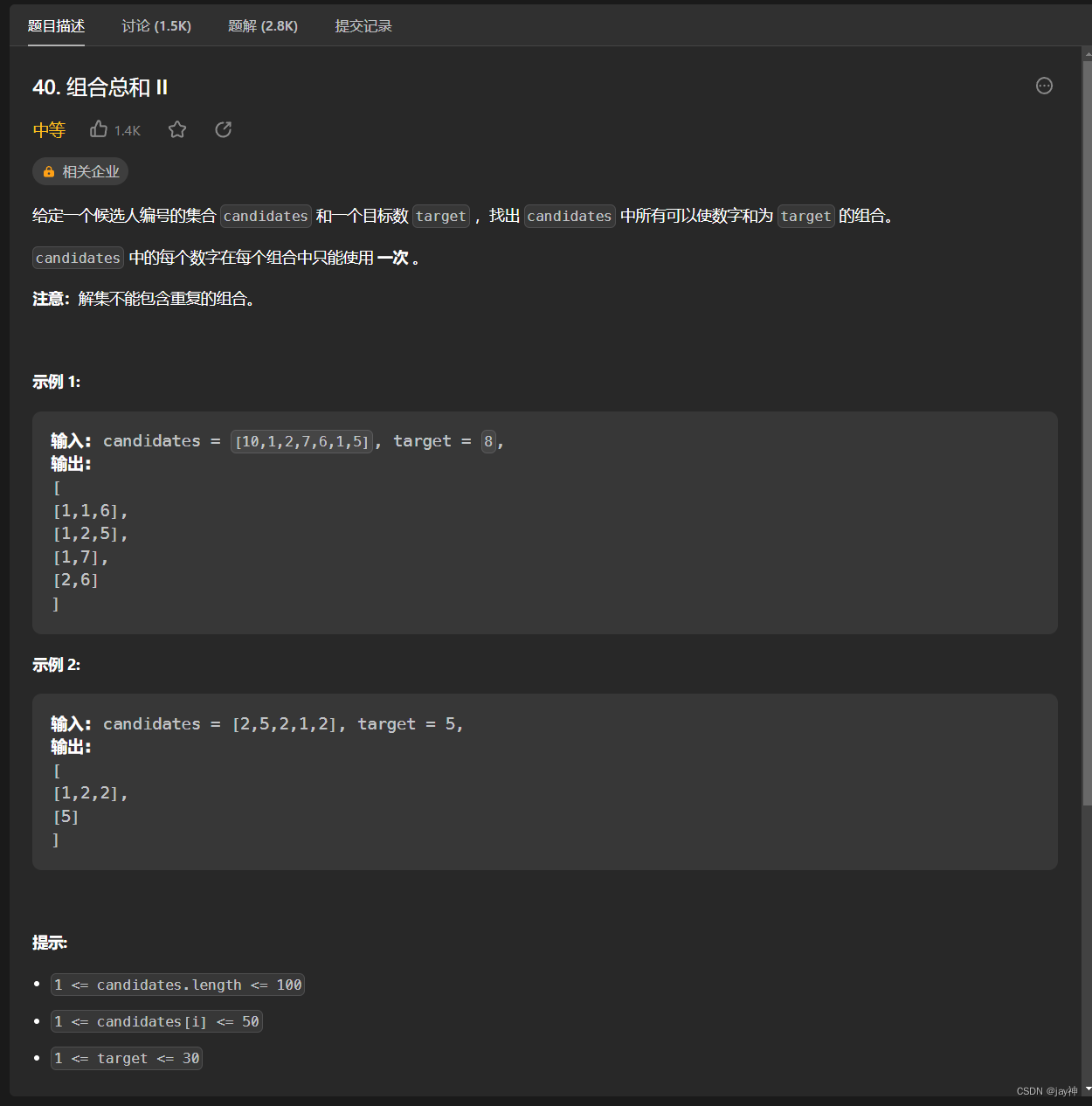
        此题为 组合总和 的升级版。本题的特殊之处在于 给定的candidates数组只一个无序且包含重复元素的数组，并且最终的解集不能包含重复的组合。

        所以本题的关键在于去重。那么，此类题的去重分为两种，一种是解集内部去重，灵一种是解集之间的去重。

        解集内部去重指不允许存在诸如{1，1，6}的解集，本题题意说了，candidates中的每个数字在每个组合中只能使用一次，所以解集内部是需要去重的，去重方法在组合总和已经使用过，即在递归的时候，将start_index+1即可。有人可能会问示例中输出为什么有解集{1，1，6}？ 那是因为candidates数组本身就存在重复的元素，也就是说两个1其实不是同一个1。

        解集之间去重指不允许存在{1，1，6}和{1，6，1}这样的重复解集，于是代码之中需要加一条去重的判断逻辑。 如果把回溯过程想象成树的话，那么解集之间去重就是指树的横切面不能有相同的元素。下面直接看代码：

class Solution {
public:vector<vector<int>> ans;vector<int> path;void backtrating(vector<int> candidates,int target,int sum,int start_index){if(sum == target){ans.push_back(path);return;}if(sum > target) return;for(int i=start_index; i<candidates.size(); i++){if(i>start_index && candidates[i]==candidates[i-1]) continue;//解集间去重path.push_back(candidates[i]);sum += candidates[i];backtrating(candidates,target,sum,i+1);//解集内部去重sum -= candidates[i];path.pop_back();}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());backtrating(candidates,target,0,0);return ans;}
};

---

2023.7.23

        也可以定义一个used数组，判别当前元素是否在树枝上使用过，如果没有那么就在树层上产生重复元素，看代码：

class Solution {
public:vector<vector<int>> ans;vector<int> path;void backtrating(vector<int> candidates,int target,int sum,int start_index,vector<bool>&used){if(sum == target){ans.push_back(path);return;}if(sum > target) return;for(int i=start_index; i<candidates.size(); i++){//if(i>start_index && candidates[i]==candidates[i-1]) continue;//树层去重if(i>0 && candidates[i]==candidates[i-1] && used[i-1]==false) continue;used[i]=true;path.push_back(candidates[i]);sum += candidates[i];backtrating(candidates,target,sum,i+1,used);sum -= candidates[i];path.pop_back();used[i]=false;}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());vector<bool> used(candidates.size(),false);backtrating(candidates,target,0,0,used);return ans;}
};

        这种方式效率低一点，但是更好理解。