场的概念 | 方向导数与梯度 | 通量与散度 | 环量与旋度 | 典型矢量场 | 哈密顿算子

• 场的概念

1.场：如果在全部空间或部分空间里的每一点，都对应着某个物理量的一个确定的值，即在这个空间里确定了该物理量的一个场。（数量场/矢量场 、稳定场/不稳定场）

2.数量场的等值面：数量场u=u(M)（即u=u(x,y,z)），由场中使函数u取相同数值的点所组成的曲面（假设这个函数单值连续且具有连续一阶偏导数，由隐函数存在定理，各连续偏导数不全为零时，这种等值面一定存在）同理可定义等值线

3.矢量场的矢量线：每一点都与对应于该点的矢量相切的曲线（在流体力学中，此为流线定义） 矢量线需满足的微分方程

（Ax,Ay,Az为场矢量坐标分量）

4.矢量场矢量面：对于场中任意一条曲线C（非矢量线），在其上每一点处，有且仅有一条矢量线经过，这些矢量线构成矢量面，特别地，当曲线C为封闭曲线时，通过C的矢量面构成管型曲面（矢量管）

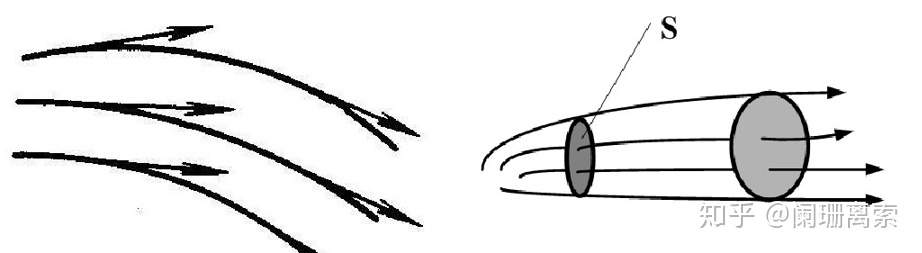
5.平行平面场：常见的、具有一定几何特点的场

平行平面矢量场：场内所有矢量均平行于某一平面q；在垂直于平面q的任一直线的所有点上，矢量的大小和方向都相同

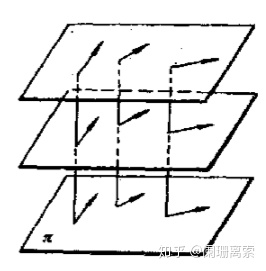
平行平面数量场：垂直于场中某一直线l的所有平行平面上，数量u的分布情况都是相同的， 或者说，在场中与直线l平行的任意一条直线的所有点上，数量u都相同

• 方向导数与梯度（数量场）

1.方向导数：设

为数量场u=u(M)中的一点，从点

出发引出一条射线l，在l上点

的邻近取一动点M，记

=p，若当

趋近于M时，比式

的 极限存在，则称此极限为函数在点

处沿l方向的方向导数，记作

（方向导数即为在某一个点

处沿方向l，函数对距离的变化率）

2.在直角坐标系中，若函数u=u(x,y,z)在点M0(x0,y0,z0)处可微，则函数u在点M0处沿l方向的偏导数必存在且其数值由如下公式给出

，

，

为方向l的方向余弦

3.若在有向曲线C上取定一点

作为计算弧长s的起点，并以C之正向作为s增大的方向；M为C上的一点，在点M处沿C之正向作一与C相切的射线l，则当u在点M处可微，曲线C光滑时时，有

; （

为函数u在点M处沿曲线C正向的方向导数）

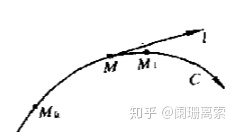
4.梯度：若在数量场u(M)中的一点处，存在这样一个矢量G，其方向为函数u(M)在M点处变化率最大的方向，其模也正好是这个最大变化率的数值，则称G为函数u(M)在点M处的梯度，记作

u，即

u=

5.梯度性质：函数u沿l方向的方向导数等于梯度在该方向上的投影；数量场u(M)中每一点M处的梯度垂直于过该点的等值面，且指向函数u(M)增大的一方，即等值面上任意一点处的单位法矢量n可定义为

；梯度运算的基本法则和微分运算法则一致。

• 通量与散度（矢量场）

1. 简单曲线：没有重点的连续曲线；简单曲面：没有重点的连续曲面。

2. 有向曲面：取定外侧为正侧的曲面

3. 通量：设有矢量场A(M)，沿其中有向曲面S某一侧的曲面积分

（矢量场

若封闭曲面s通量大于零，则s内存在源，反之则说明s内有汇。

4. 散度：设有矢量场A(M)，于场中一点M的某个邻域内作一包含M点的任意闭曲面

，设其所包围的空间区域为

，以

表示其体积，以

表示从其内穿出S的通量。若当

以任意方式缩向点M时，比式

极限存在，则称此极限为矢量场

散度div A为纯量，表示场中一点处通量对体积的变化率，即该点处对一个单位体积来说所穿出之通量，即该处源的强度；div A=0时，矢量场A为无源场

在直角坐标系中，

5. 散度运算基本法则

（c为常数，u为数性函数）

6. 通量与散度关系：

7. 平面矢量场法向矢量：规定其沿逆时针旋转 90度与切向矢量重合

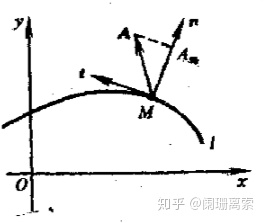
8. 平面矢量场的通量：平面矢量场

中沿其中某一有向曲线

的曲线积分

（对于封闭曲线，总是规定逆时针方向为正向）

9.平面矢量场的散度：设有平面矢量场

，于场中一点M的某个邻域内作一包含M点在内的任一闭曲线

，设其所包围平面区域为

，以

表示其面积，以

表示其从内穿出

的通量。若当

以任意方式缩向M点时，比式

的极限存在，则称此极限为矢量场A在点M处的散度。

• 环量与旋度（矢量场）

1. 环量：沿矢量场A中某一封闭的有向曲线l的曲线积分

2. 环量面密度：设M为矢量场A中一点，在点M处取定一个方向n，再过点M作任一微小曲面

，以

为其在点M处的法矢量，此曲面周界

与

构成右手螺旋关系，定义

的极限为环量面密度

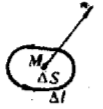
在直角坐标系下

3. 旋度：若在矢量场A中的一点M处存在这样一个矢量

，矢量场A在点M处沿其方向的环量面密度为最大，这个数值，正好就是

，则称矢量

为矢量场A在M处的旋度，记

，即

在直角坐标系中

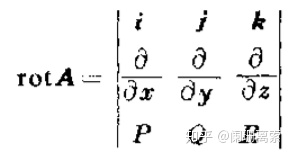
4. 旋度运算法则：

• 三种重要的矢量场（有势场、管形场、调和场）

1. 有势场：设有矢量场A(M)，若存在单值函数u(M)，满足
   ，则称这个矢量场为有势场，令v=-u，则v为这个场的势函数。

1）有势场是一个梯度场；有势场的势函数有无穷个，它们之间只差一个常数

2）在线单连域内矢量场A为有势场的充要条件时A为无旋场

3）“场有势”“场无旋（rot A=0）”“场保守（场内曲线积分与路径无关）”彼此等价

2.管形场：设有矢量场A(M)，若其散度div A=0，则称这个矢量场为管形场（即为无源场）。

1） 在面单连域内矢量场A为管形场的充要条件：A为另一个矢量场B的旋度场，即

，满足条件的矢量场B，称为矢量场A的矢势量。

2） 设管形场A所在的空间区域为一面单连域，在场中任取一个矢量管。假定

和

时它的任意两个横断面，其法向量

和

都朝向矢量A所指的一侧，则有

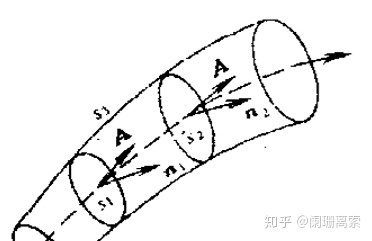
3. 调和场：如果在矢量场A中恒有

和

，称此矢量场为调和场

1）势函数u为调和函数，满足拉普拉斯方程

为方便表述，我们引入微分算子

2）平面调和场：定义u为平面调和场A的力函数，则u与v构成共轭调和函数

• 哈密顿算子

1.引入哈密顿算子

引入数性微分算子

2. 运算规则

即

3. 奥斯特罗格拉茨基公式

4.格林公式

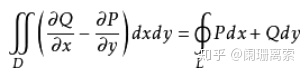
（格林公式推广至三维即为斯托克斯公式）

5. 斯托克斯公式

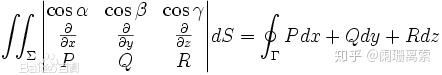
4. 一些常见的公式（c为常数，

为常矢，u、v为数性函数，

、

为矢性函数）

5. 若

，则

（原方向上的单位矢量）

2019.12.19 BUAA Old Building

2019.12.20 BUAA Lib

2019.12.21 BUAA Dorm

/Elisabeth 2001 Essen Cast Recording/

/Cats Original Broadway Cast Recording/

/Mozart L'opera Rock Complete Recording/