读完本文，你可以去力扣拿下如下题目：

222.完全二叉树的节点个数

-----------

如果让你数一下一棵普通二叉树有多少个节点，这很简单，只要在二叉树的遍历框架上加一点代码就行了。

但是，如果给你一棵完全二叉树，让你计算它的节点个数，你会不会？算法的时间复杂度是多少？这个算法的时间复杂度应该是 O(logN*logN)，如果你心中的算法没有达到高效，那么本文就是给你写的。

首先要明确一下两个关于二叉树的名词「完全二叉树」和「满二叉树」。

我们说的完全二叉树如下图，每一层都是紧凑靠左排列的：

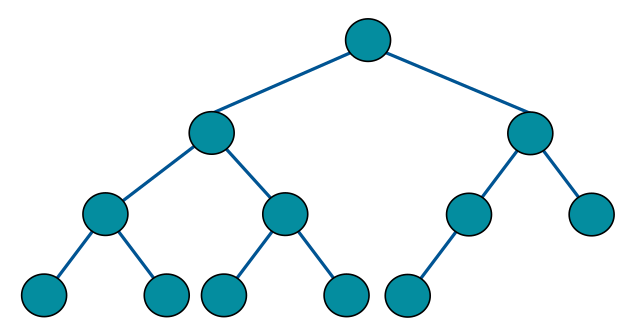
我们说的满二叉树如下图，是一种特殊的完全二叉树，每层都是是满的，像一个稳定的三角形：

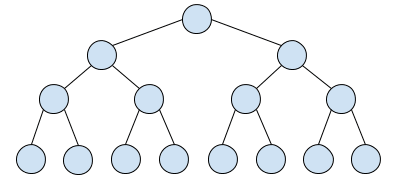
说句题外话，关于这两个定义，中文语境和英文语境似乎有点区别，我们说的完全二叉树对应英文 Complete Binary Tree，没有问题。但是我们说的满二叉树对应英文 Perfect Binary Tree，而英文中的 Full Binary Tree 是指一棵二叉树的所有节点要么没有孩子节点，要么有两个孩子节点。如下：

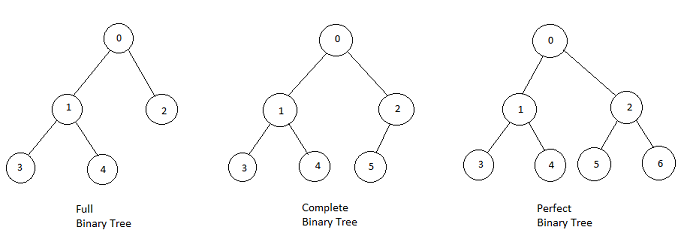
以上定义出自 wikipedia，这里就是顺便一提，其实名词叫什么都无所谓，重要的是算法操作。本文就按我们中文的语境，记住「满二叉树」和「完全二叉树」的区别，等会会用到。

一、思路分析

现在回归正题，如何求一棵完全二叉树的节点个数呢？

// 输入一棵完全二叉树，返回节点总数
int countNodes(TreeNode root);

如果是一个普通二叉树，显然只要向下面这样遍历一边即可，时间复杂度 O(N)：

public int countNodes(TreeNode root) {if (root == null) return 0;return 1 + countNodes(root.left) + countNodes(root.right);
}

那如果是一棵满二叉树，节点总数就和树的高度呈指数关系：

public int countNodes(TreeNode root) {int h = 0;// 计算树的高度while (root != null) {root = root.left;h++;}// 节点总数就是 2^h - 1return (int)Math.pow(2, h) - 1;
}

完全二叉树比普通二叉树特殊，但又没有满二叉树那么特殊，计算它的节点总数，可以说是普通二叉树和完全二叉树的结合版，先看代码：

public int countNodes(TreeNode root) {TreeNode l = root, r = root;// 记录左、右子树的高度int hl = 0, hr = 0;while (l != null) {l = l.left;hl++;}while (r != null) {r = r.right;hr++;}// 如果左右子树的高度相同，则是一棵满二叉树if (hl == hr) {return (int)Math.pow(2, hl) - 1;}// 如果左右高度不同，则按照普通二叉树的逻辑计算return 1 + countNodes(root.left) + countNodes(root.right);
}

结合刚才针对满二叉树和普通二叉树的算法，上面这段代码应该不难理解，就是一个结合版，但是其中降低时间复杂度的技巧是非常微妙的。

PS：我认真写了 100 多篇原创，手把手刷 200 道力扣题目，全部发布在labuladong的算法小抄，持续更新。建议收藏，按照我的文章顺序刷题，掌握各种算法套路后投再入题海就如鱼得水了。

二、复杂度分析

开头说了，这个算法的时间复杂度是 O(logN*logN)，这是怎么算出来的呢？

直觉感觉好像最坏情况下是 O(N*logN) 吧，因为之前的 while 需要 logN 的时间，最后要 O(N) 的时间向左右子树递归：

return 1 + countNodes(root.left) + countNodes(root.right);

关键点在于，这两个递归只有一个会真的递归下去，另一个一定会触发 hl == hr 而立即返回，不会递归下去。

为什么呢？原因如下：

一棵完全二叉树的两棵子树，至少有一棵是满二叉树：

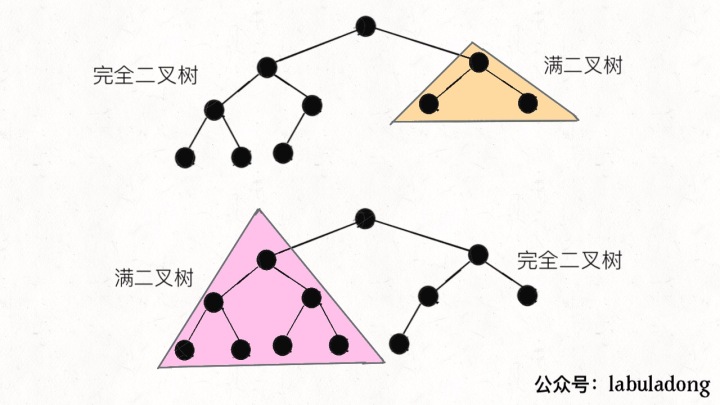
看图就明显了吧，由于完全二叉树的性质，其子树一定有一棵是满的，所以一定会触发 hl == hr，只消耗 O(logN) 的复杂度而不会继续递归。

综上，算法的递归深度就是树的高度 O(logN)，每次递归所花费的时间就是 while 循环，需要 O(logN)，所以总体的时间复杂度是 O(logN*logN)。

所以说，「完全二叉树」这个概念还是有它存在的原因的，不仅适用于数组实现二叉堆，而且连计算节点总数这种看起来简单的操作都有高效的算法实现。

＿＿＿＿＿＿＿＿＿＿＿＿＿

我的 在线电子书 有 100 篇原创文章，手把手带刷 200 道力扣题目，建议收藏！对应的 GitHub 算法仓库 已经获得了 70k star，欢迎标星！