python实现常见排序算法
快速排序
思想:取出第一个元素把它放到序列的中间某一个正确位置,以它进行分割成左边和右边,再分别对左边和右边进行取元素分割(递归)
递归实现
def quicksort(array):if len(array) < 2: # 递归终止条件:数组少于2则是一个元素或空元素无需排序return arrayelse:mid = array[0] # 先确定一个中间点less = [i for i in array[1:] if i <= mid] # 生成一个列表的元素全部小于等于中间基准点more = [i for i in array[1:] if i > mid] # 生成一个列表的元素全部大于中间基准点return quicksort(less) + [mid] + quicksort(more) # 列表拼接,左边继续调用自身排序,右边同理#验证结果
print(quicksort([1, 4, 2, 6, 4, 5, 8, 3]))
#===>[1, 2, 3, 4, 4, 5, 6, 8]
时间复杂度
- 最优时间复杂度:O(nlogn)
- 最坏时间复杂度:O(n*n) ==>深度最坏的n,单层是n,所以n*n
- 稳定性:不稳定
对O(nlogn)的类比通俗理解:
递归调用函数可以理解为二叉树,调用树的深度是O(log n),也就是要切分logn次,而调用的每一层次结构总共全部仅需要O(n)的时间,所以二者相乘得O(nlogn),我这里说的调用树其实是调用栈后面也会详细说道快速排序的时间复杂度。
在最好的情况,每次我们运行一次分区,我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。
选择排序
思想: 假设最后一个元素是最大值,现在要从左到右(除了最后一个)依次与最大值进行比较,如果大于最大值就将两个位置进行交换。
代码实现
def selection_sort(array):for i in range(len(array)-1,0,-1): #产生[n-1,n-2,...2,1]for j in range(i):if array[j] > array[i]:array[j], array[i] = array[i], array[j]return array
时间复杂度
- 最优时间复杂度:O(n*n)
- 最坏时间复杂度:O(n*n) ==>深度最坏的n,单层是n,所以n*n
- 稳定性:不稳定
冒泡排序
思想:所谓冒泡,就是将元素两两之间进行比较,谁大就往后移动,直到将最大的元素排到最后面,接着再循环一趟,从头开始进行两两比较,而上一趟已经排好的那个元素就不用进行比较了。
一级优化实现
考虑整数数组就是有序的特殊情况,设定一个变量为False,如果元素之间交换了位置,将变量重新赋值为True,最后再判断,在一次循环结束后,变量如果还是为False,则break退出循环,结束排序。
def bubble_sort(array):for i in range(len(array) - 1): # 外层循环n次保证所有数都在正确的位置上flag = False # 标识for j in range(len(array) - 1 - i): #内层循环一次代表最后一个数就是最大的if array[j] > array[j + 1]:array[j], array[j + 1] = array[j + 1], array[j]flag = True # 只要需要进行交换,则进入循环改为Trueif not flag: #如果没进入循环体说明原来的数据是有序的break # 直接跳出循环return array
二级优化实现
上面这种写法还有一个问题,就是每次都是从左边到右边进行比较,这样效率不高,你要考虑当最大值和最小值分别在两端的情况。写成双向排序提高效率,即当一次从左向右的排序比较结束后,立马从右向左来一次排序比较。
def bubble_sort(array):for i in range(len(array) - 1):flag = Falsefor j in range(len(array) - 1 - i):if array[j] > array[j + 1]:array[j], array[j + 1] = array[j + 1], array[j]flag = Trueif flag: # 上个循环体循环一次保证最后一个数是最大的flag = False for j in range(len(array) - 2 - i, 0, -1): # 从倒数第二个数开始,从后往前再浮动比较一下if array[j - 1] > array[j]:array[j], array[j - 1] = array[j - 1], array[j]flag = Trueif not flag:breakreturn array
时间复杂度
- 最优时间复杂度:O(n) ==> 已经是有序的了
- 最坏时间复杂度:O(n*n)
- 稳定性:稳定==>每次判断如果相等,那就不交换,位置不变
插入排序
思想:认定第一个元素是有序,取出第二个元素进行判断插入到左边的正确位置上,这是一个内循环,外循环遍历不包括第一个元素的下标进行重复操作。
def insert_sort(array):for i in range(1, len(array)): j = i # 从第二个元素开始while j > 0 :if array[j-1] > array[j]:array[j-1], array[j] = array[j], array[j-1]j -= 1else: # 如果操作就是有序序列,每次都执行else退出循环体,提升效率break
时间复杂度
- 最优时间复杂度:O(n)
- 最坏时间复杂度:O(n*n)
- 稳定性:稳定==> 如果数值相等,在代码中对=不进行处理,所以也不交换位置保证原来的位置顺序
归并排序:
思路:将数组拆分成一个一个的小数组,然后进行临近合并,合并的时候进行判断排序
递归实现
def merge(left, right):"""合并排序"""L, R = 0, 0slist = []while L < len(left) and R < len(right):if left[L] <= right[R]:slist.append(left[L])L += 1else:slist.append(right[R])R += 1# 循环体结束,对称的数据都比较完了,可能出现不对称的话,将剩余数据追加到slist中slist += left[L:]slist += right[R:]return slist
def merge_sort(arr):if len(arr) < 2:return arr# 开始递归拆分数组mid = len(arr) // 2left_list = merge_sort(arr[:mid])right_list = merge_sort(arr[mid:])# 开始合并return merge(left_list,right_list)
时间复杂度
- 最优时间复杂度:O(nlogn)
- 最坏时间复杂度:O(nlogn)
- 稳定性:稳定
排序算法时空复杂度总结
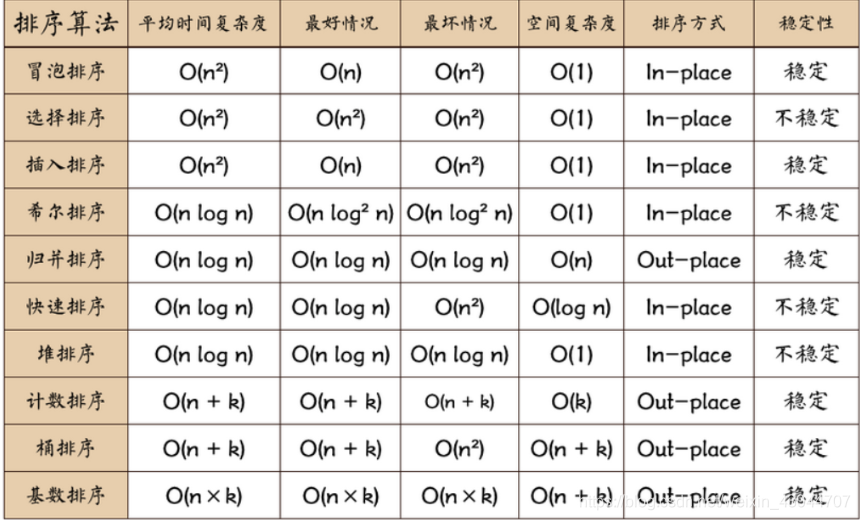
这里只说一下快速排序和归并排序
快速排序我们递归调用栈的思想来理解,结合我后一篇文章学习递归来理解。
最好的情况, 快速排序的每次选的中间值mid都是真正的中间值,调用栈的高度(函数调用层数)就为O(logn),而每层需要时间为O(n),因此整个算法需要的时间为O(n) * O(log n) = O(n log n)。这就是最佳情况。
最糟糕情况, 有O(n)层,因此该算法的运行时间为O(n) * O(n) = O(n2)。
最佳情况也是平均情况。 只要你每次都随机地选择一个数组元素作为基准值,快速排序的平均运行时间就将为O(n log n)。快速排序是最快的排序算法之一,也是D&C(分而治之)典范。
这里需要记住的是,快速排序一般情况下是比归并排序的速度要快
渲染架构)

几何变换)

图层树结构)

图层内容)

动画)
图层Action)

事务)

图层布局)

KVC)

)

