题目:
实现一个函数,输入一个整数,输出该数二进制中1的个数。例如把9表示成二进制是1001,有2位是1,因此如果输入是9,该函数输出2
第一种解法(死循环)
- 判断整数二进制表示中最右边的一位是不是1
- 将二进制数右移一位¹
- 直到整个整数变成0为止
代码如下:
int NumberOf1(int n)
{ int count = 0; while(n){ if(n & 1) count++; n = n >> 1; } return count;}这样很容易造成死循环,如果输入是一个负数,将负数想右移一位的时候,并不是简单的将最高位1移到第二位,而是移位后最高位任然回事1,因为右移前是一个负数,右移后仍要保持是负数,一直持续下去数字就会变成0xFFFFFFFF而陷入死循环
第二种解法(常规)
为了避免死循环,可以不移动输入的数字,移动一个无符号的变量1
- 定义一个无符号的临时变量tmp = 1
- 将输入的数字与tmp做位与运算,判断最低位是不是1
- 将tmp左移一位,再次将输入的数字与tmp做位与运算,判断次低位是不是1
- 将tmp一直左移,直到最高位
代码如下:
int NumberOf1(int n){int count = 0;unsigned int tmp = 1;while (tmp){if (n & tmp){count++;}tmp = tmp << 1;}return count;}
这样效率相对低一些,因为这个循环次数等于整数二进制的位数,32位的整数就需要循环32次,浪费不必要的时间
第三种解法(将以上优缺点进行了融合)
为了提高代码的效率,可以将整数减1在与之前的原整数进行位与运算
- 将输入的整数减1再与原整数进行位与运算
- 将运算结果赋给输入的整数
- 一直循环1、2,直到这个整数为零
代码如下:
int NumberOf2(int n){ int count = 0;while (n){n = n&(n - 1);count++;}return count;}
这种解法可以有效的避免死循环和效率低,例如1101,具体实现过程如下
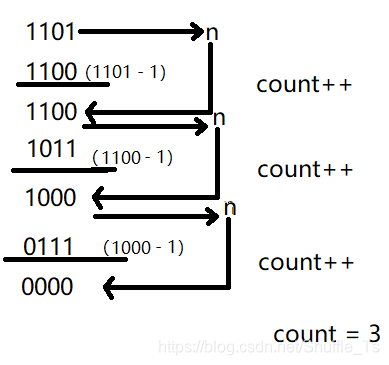
注:1、不能用除法来代替移位,因为除法的效率比移位运算要低得多,应该多用移位来代替除法


)
)















