题目解析：
队伍的水平值等于该队伍队员中第二高水平值，为了所有队伍的水平值总和最大的解法，也就是说每个队伍的第二个值是尽可能大的值。所以实际值把最大值放到最右边，最小是放到最左边。
解题思路：
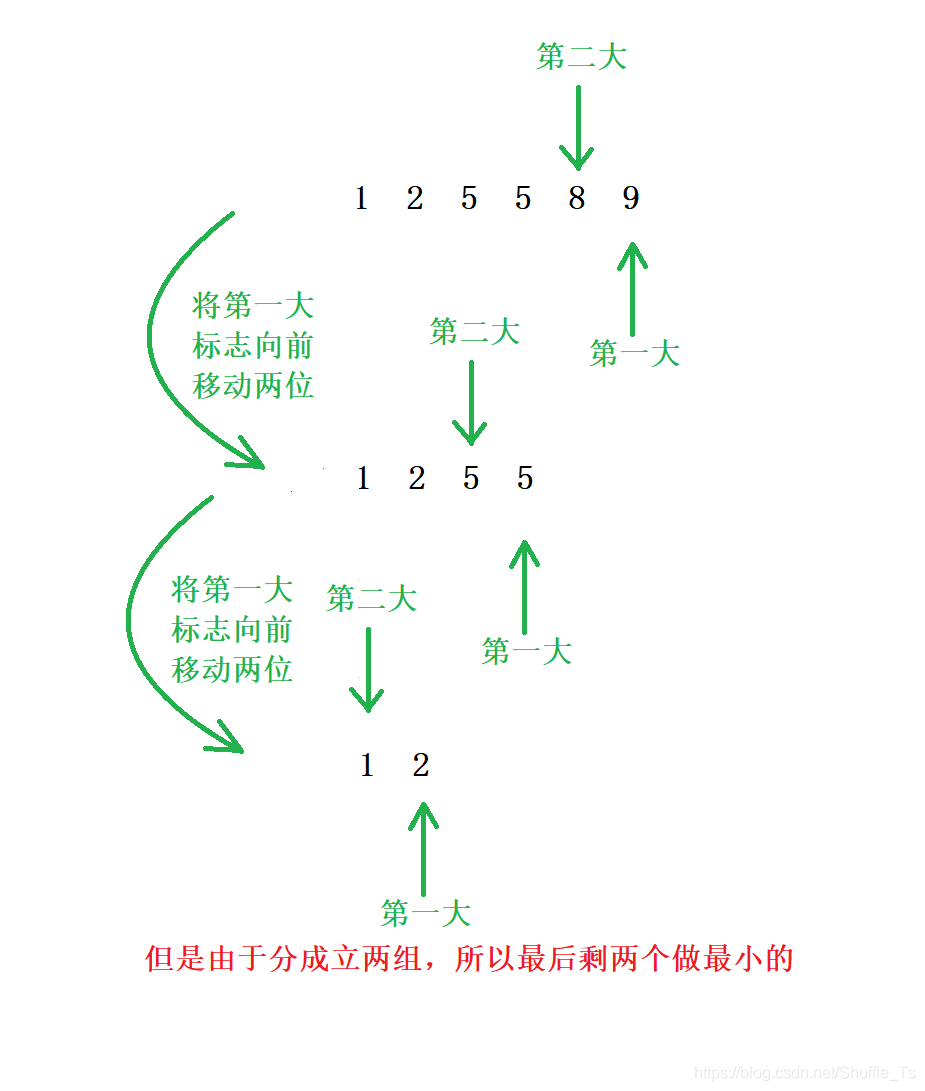
本题的主要思路是贪心算法，贪心算法其实很简单，就是每次选值时都选当前能看到的局部最解忧，所以这里的贪心就是保证每组的第二个值取到能选择的最大值就可以，我们每次尽量取最大，但是最大的数不可能是中位数，所以退而求其次，取 每组中第二大的排序，然后取下标为3n - 2，3n - 4 ，3n - 6… n+2，n位置的元素累加即可，相当下标为[0,n-1]的n个数做每组的最左边的数，剩下的2个数据两个为一组，大的值做最右边的数，次大的做中间值，这里就是把这个次大的值加起来。
例如 现在排序后 有 1 2 5 5 8 9 ，那么取 8 和 5相加等于 13
图解思路：

上代码：

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int main()
{int n = 0;long long sum = 0;	//这里需要注意一下，如果将sum定义为int类型可能会超出int的存储范围std::vector<int> arr;std::cin >> n;        arr.resize(n*3);for(auto i = 0; i < n*3; ++i)        cin >> arr[i];sort(arr.begin(),arr.end());         //对成员的成绩进行排序 //for (int i = 3 * n - 2; i >= n; i -= 2) //这个是按照图解定义的循环，for (int i = n; i <= 3 * n - 2; i += 2)   //下面是我个人风格，习惯将i的初始化简单一些  {sum += arr[i];}cout << sum << endl;return 0;
}