我们现在知道原则上4对匹配点对就可以唯一确定单应矩阵,但是在实际应用中我们无法保证两个视图严格满足使用条件(只有旋转变换;远景;平面场景),所以要使用拟合的方法求一个最优解。现在就来以SIFT算法源码为例,看一下是怎么求解的。这是RobHess写的SIFT源码中求解矩阵的代码部分,我们依次看每一个参数的含义:
H1 = ransac_xform( feat1, n1, FEATURE_FWD_MATCH, lsq_homog, 4, 0.01,//求变换矩阵用4对匹配对homog_xfer_err, 3.0, NULL, NULL );//允许错误概率为0.01
第一个参数是指向struct feature的指针。
第二个参数是图1中特征点的数目。结合第一个参数和函数get_matched_features找到特征点1对应的匹配对CvPoint2D64f* pts, * mpts,要求至少有4对匹配对。
第三个参数决定使用每个特征点的哪个匹配域进行变换矩阵的计算,对应的匹配点对是每个特征点的img_pt域和其匹配点的img_pt域
第四个参数xform_fn:函数指针,指向根据输入的点对进行变换矩阵计算的函数,一般传入lsq_homog()函数。lsq_homog()函数会根据CvPoint2D64f* pts, * mpts利用RANSAC计算单应矩阵。源码的注释中有这么两句话:Returns the 3 x 3 least-squares planar homography matrix.Calculates a least-squares planar homography from point correspondeces.
这就到了今天的重点:
CvMat* lsq_homog( CvPoint2D64f* pts, CvPoint2D64f* mpts, int n )
{CvMat* H, * A, * B, X;double x[9];int i;if( n < 4 ){fprintf( stderr, "Warning: too few points in lsq_homog(), %s line %d\n",__FILE__, __LINE__ );return NULL;}/* set up matrices so we can unstack homography into X; AX = B */A = cvCreateMat( 2*n, 8, CV_64FC1 );//2*n行,8列B = cvCreateMat( 2*n, 1, CV_64FC1 );X = cvMat( 8, 1, CV_64FC1, x );//8行一列,初始值为x,x是一个数组指针H = cvCreateMat(3, 3, CV_64FC1);cvZero( A );for( i = 0; i < n; i++ ){cvmSet( A, i, 0, pts[i].x );cvmSet( A, i+n, 3, pts[i].x );cvmSet( A, i, 1, pts[i].y );cvmSet( A, i+n, 4, pts[i].y );cvmSet( A, i, 2, 1.0 );cvmSet( A, i+n, 5, 1.0 );cvmSet( A, i, 6, -pts[i].x * mpts[i].x );cvmSet( A, i, 7, -pts[i].y * mpts[i].x );cvmSet( A, i+n, 6, -pts[i].x * mpts[i].y );cvmSet( A, i+n, 7, -pts[i].y * mpts[i].y );cvmSet( B, i, 0, mpts[i].x );cvmSet( B, i+n, 0, mpts[i].y );}cvSolve( A, B, &X, CV_SVD );x[8] = 1.0;X = cvMat( 3, 3, CV_64FC1, x );cvConvert( &X, H );cvReleaseMat( &A );cvReleaseMat( &B );return H;
}
lsq_homog()函数中的B很容易理解,就是2nx1的列向量,存放图2中匹配点的坐标:
按道理A也应该是这种形式的矩阵,存放图1中的特征点,但是实际的A是这样子的:
为什么要将A变形成这种形式呢?因为在计算机中,求解非齐次方程组也是先转换成齐次方程组如AX=0,然后再转化为min ||Ax||2 的非线性优化问题(超定方程,通过最小二乘拟合得到近似解)。这也是为什么称作最小二乘求解的原因。
首先我们知道单应矩阵是3x3的矩阵,有8个自由度
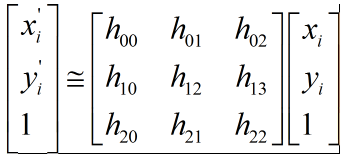

如果将H矩阵看作是一维数组,![]() ,那么我们可以很容易得到
,那么我们可以很容易得到

但是因为单应矩阵中自由度是8,h22=1,所以可以将等式中左边的矩阵的最后一列舍去,变成源码中的形式。
这里我们以AX=B为例说明一下最小二乘问题。AX=B是我们很熟悉的齐次方程,m个方程求解n个未知数,考试的时候经常考察它什么时候有唯一非零解,但是其实大多时候如机器学习中,样本数远大于特征数m>n,约束的个数大于未知数的个数,称为超定问题(overdetermined)。也就是说,X要满足的条件过于多,不可能同时满足,即没有解,只能使用如最小二乘法来拟合。
最小二乘问题:

齐次方程时最小化问题为:

即:在做最小二乘估计时,其实不需要完整进行SVD分解,只需要得到AT*A的最小特征值对应的特征向量即可。
Reference:
- https://blog.csdn.net/qq_32454557/article/details/76647374
- 刘毅的推导https://www.cnblogs.com/liufuqiang/p/5663175.html
- 称为超定问题(overdetermined)http://www.cnblogs.com/houkai/p/6656894.html
最新综述论文及相关源码)


)





)



+卷积层可视化)





