声明:文中的图来自于可汗学院公开课,若有侵权,联系我删除。
中心极限定理:随着样本容量n的增加,样本均值或者样本和的频率图将很接近正态分布。
如下图就在求解样本均值。

如下图就是样本均值的频率图,很接近正态分布。
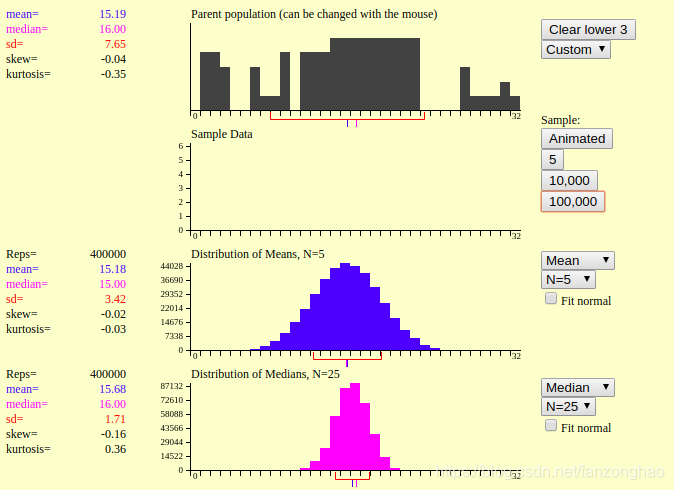
http://onlinestatbook.com/stat_sim/sampling_dist/index.html
上面网址是课程用来模拟样本均值抽样分布近似正态分布。
如图黑色是原始分布,蓝色是抽5个样本的均值分布,粉红色是抽25个样本的均值分布。可看出均值接近原始分布的均值,而方差在变小。即样本均值的抽样分布接近于均值为μ,方差为σ2/n的正态分布。
伯努利分布均值为p,方差为p(1-p)
置信区间展现的是这个参数的真实值有一定概率落在测量结果的周围的程度,其给出的是被测量参数的测量值的可信程度。误差范围是描述置信区间的另一种方法。
样本空间的均值和标准差可以用来预测总体的均值与标准差。
缩小置信区间的方法:增大样本容量,这样使样本空间标准差缩小,从而总体空间标准差缩小,以达到缩小置信区间的目的。
但是,样本容量小于30通常是糟糕的估计,当样本少的时候,要用t分布而不是正态分布表示小样本容量时的置信区间。






)












