广度优先搜索（BFS）与深度优先搜索（DFS）

一.广度优先搜索（BFS）

1.二叉树代码

# 实现一个二叉树
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = Noneself.nexts = []root_node = TreeNode(1)
node_2 = TreeNode(2)
node_3 = TreeNode(3)
node_4 = TreeNode(4)
node_5 = TreeNode(5)
node_6 = TreeNode(6)
node_7 = TreeNode(7)
node_8 = TreeNode(8)
node_9 = TreeNode(9)
node_10 = TreeNode(10)def littleTree(root, left, right):root.left = leftroot.right = rightif root.left:root.nexts.append(root.left)if root.right:root.nexts.append(root.right)# print(root.left)# print(root.right)# print(root.nexts)littleTree(root_node, node_2, node_3)
littleTree(node_2, node_4, node_5)
littleTree(node_5, node_10, None)
print('===root_node:', root_node.left)
print('===root_node:', root_node.right)
print('===root_node:', root_node.nexts)
print('===root_node.left.left:', root_node.left.left)
print('===root_node.left.right:', root_node.left.right)
print('===root_node.left.nexts:', root_node.left.nexts)

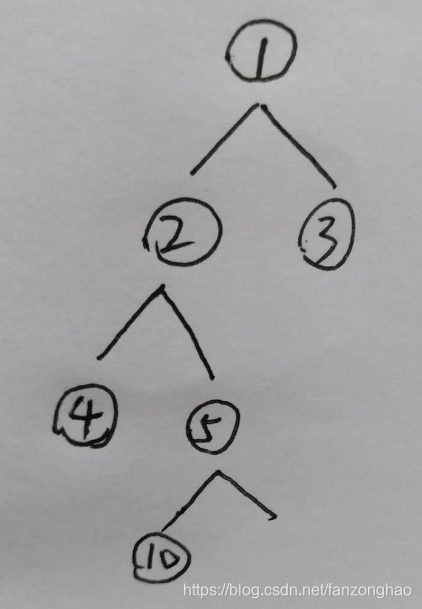
其是一层一层来，结果不唯一

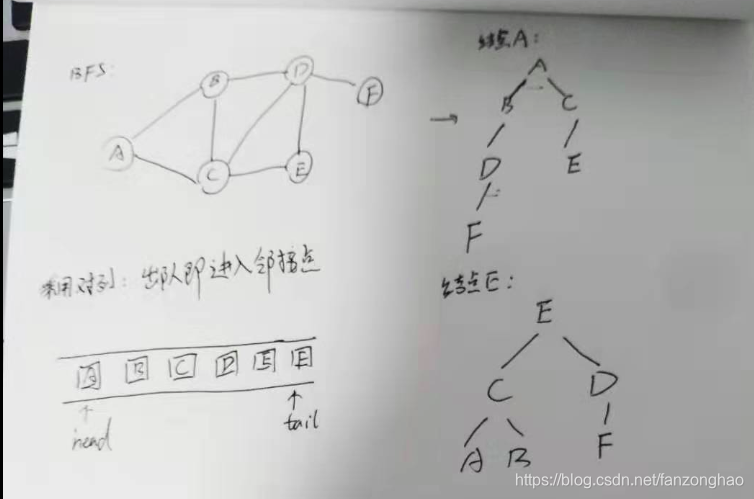
2.字典实现bfs

graph ={'A':['B', 'C'],'B':['C', 'D'],'C':['B','E'],'D':['B','E','F'],'E':['C','D'],'F':['D']}def BFS(graph,node):quene = []quene.append(node)seen = set()seen.add(node)res = []while len(quene):verix = quene.pop(0)nodes = graph[verix]for node_ in nodes:if node_ not in seen:quene.append(node_)seen.add(node_)# print('==verix:', verix)res.append(verix)return resres = BFS(graph, node='A')
print('===res:', res)

3.延展:求节点和节点之间的最短路径, 通过构建节点的前一个节点成对,
求A到E的最短路径,通过从A开始构建节点对,在从E逆序找就OK

graph ={'A':['B', 'C'],'B':['C', 'D'],'C':['B','E'],'D':['B','E','F'],'E':['C','D'],'F':['D']}#延展求节点和节点之间的最短路径, 通过构建节点的前一个节点 成对,
#求A到E的最短路径,通过从A开始构建节点对,在从E逆序找就OK
def BFS(graph,node):quene = []quene.append(node)seen = set()seen.add(node)parent={}parent[node] = Noneres = []while len(quene):verix = quene.pop(0)nodes = graph[verix]for node_ in nodes:if node_ not in seen:quene.append(node_)seen.add(node_)parent[node_] = verix# print('==verix:', verix)res.append(verix)return res,parentres, parent = BFS(graph, node='A')
print('===res:', res)
print('===parent', parent)#求A到E的最短路径
v = 'E'
while v is not None:print('v:', v)v = parent[v]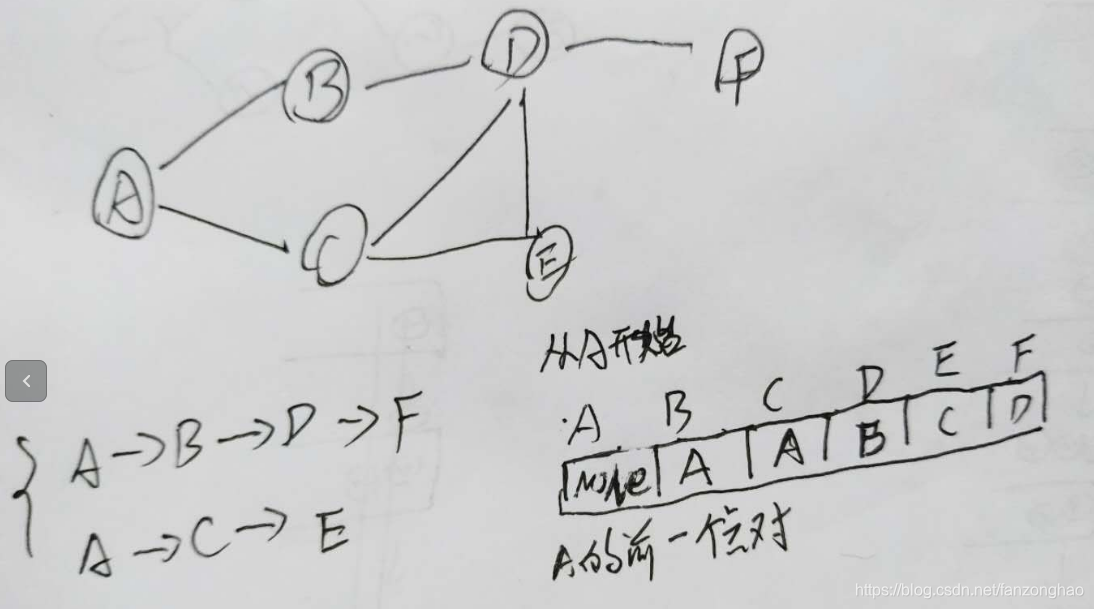

4.BFS代码二叉树实现

# 实现一个二叉树
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = Noneself.nexts = []root_node = TreeNode(1)
node_2 = TreeNode(2)
node_3 = TreeNode(3)
node_4 = TreeNode(4)
node_5 = TreeNode(5)
node_6 = TreeNode(6)
node_7 = TreeNode(7)
node_8 = TreeNode(8)
node_9 = TreeNode(9)
node_10 = TreeNode(10)def littleTree(root, left, right):root.left = leftroot.right = rightif root.left:root.nexts.append(root.left)if root.right:root.nexts.append(root.right)# print(root.left)# print(root.right)# print(root.nexts)littleTree(root_node, node_2, node_3)
littleTree(node_2, node_4, node_5)
littleTree(node_5, node_10, None)
print('===root_node:', root_node.left)
print('===root_node:', root_node.right)
print('===root_node:', root_node.nexts)
print('===root_node.left.left:', root_node.left.left)
print('===root_node.left.right:', root_node.left.right)
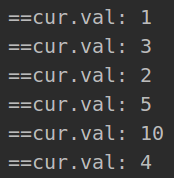
print('===root_node.left.nexts:', root_node.left.nexts)def bfs(node):if node is None:returnqueue = []#nodeSet = set()queue.insert(0, node)#nodeSet.add(node)print('==queue:', queue)while queue:cur = queue.pop()            # 弹出元素print('==cur.val:', cur.val)# 打印元素值for next in cur.nexts:    # 遍历元素的邻接节点queue.insert(0, next)bfs(root_node)

构建的二叉树 bfs遍历为:1-2-3-4-5-10

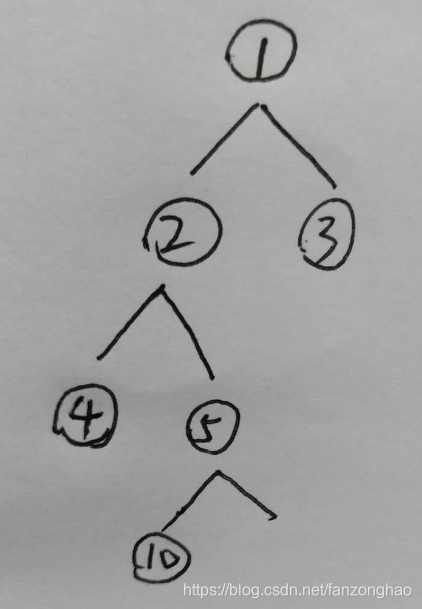
二.深度优先搜索（DFS）

其是一条路走到黑，结果不唯一

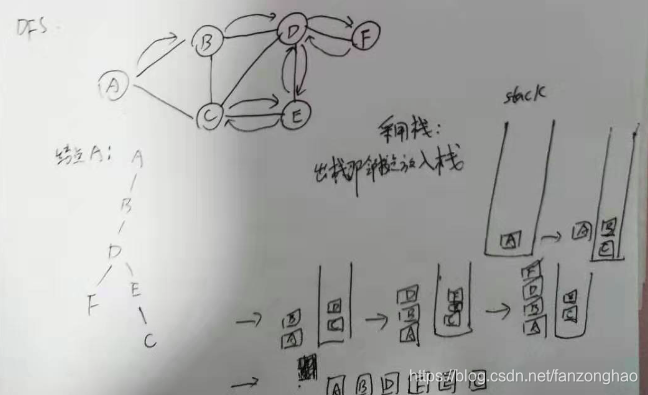
graph ={'A':['B', 'C'],'B':['C', 'D'],'C':['B','E'],'D':['B','E','F'],'E':['C','D'],'F':['D']}def DFS(graph,node):stack = []stack.append(node)seen = set()seen.add(node)res = []while len(stack):verix = stack.pop()nodes = graph[verix]for node_ in nodes:if node_ not in seen:stack.append(node_)seen.add(node_)# print('==verix:', verix)res.append(verix)return resres = DFS(graph, node='A')
print('===res:', res)

1.dfs递归写法

# 实现一个二叉树
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = Noneself.nexts = []root_node = TreeNode(1)
node_2 = TreeNode(2)
node_3 = TreeNode(3)
node_4 = TreeNode(4)
node_5 = TreeNode(5)
node_6 = TreeNode(6)
node_7 = TreeNode(7)
node_8 = TreeNode(8)
node_9 = TreeNode(9)
node_10 = TreeNode(10)def littleTree(root, left, right):root.left = leftroot.right = rightif root.left:root.nexts.append(root.left)if root.right:root.nexts.append(root.right)# print(root.left)# print(root.right)# print(root.nexts)littleTree(root_node, node_2, node_3)
littleTree(node_2, node_4, node_5)
littleTree(node_5, node_10, None)
print('===root_node:', root_node.left)
print('===root_node:', root_node.right)
print('===root_node:', root_node.nexts)
print('===root_node.left.left:', root_node.left.left)
print('===root_node.left.right:', root_node.left.right)
print('===root_node.left.nexts:', root_node.left.nexts)#递归实现dfs
def dfs1(node):if node is None:return Noneprint('==node.val:', node.val)for next in node.nexts:dfs1(next)dfs1(root_node)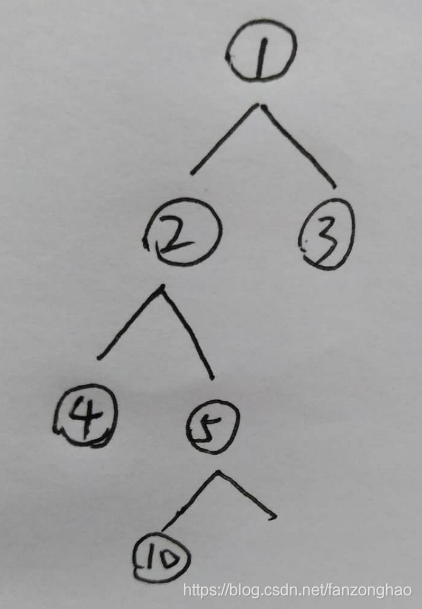

2.dfs压栈写法

# 实现一个二叉树
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = Noneself.nexts = []root_node = TreeNode(1)
node_2 = TreeNode(2)
node_3 = TreeNode(3)
node_4 = TreeNode(4)
node_5 = TreeNode(5)
node_6 = TreeNode(6)
node_7 = TreeNode(7)
node_8 = TreeNode(8)
node_9 = TreeNode(9)
node_10 = TreeNode(10)def littleTree(root, left, right):root.left = leftroot.right = rightif root.left:root.nexts.append(root.left)if root.right:root.nexts.append(root.right)# print(root.left)# print(root.right)# print(root.nexts)littleTree(root_node, node_2, node_3)
littleTree(node_2, node_4, node_5)
littleTree(node_5, node_10, None)
print('===root_node:', root_node.left)
print('===root_node:', root_node.right)
print('===root_node:', root_node.nexts)
print('===root_node.left.left:', root_node.left.left)
print('===root_node.left.right:', root_node.left.right)
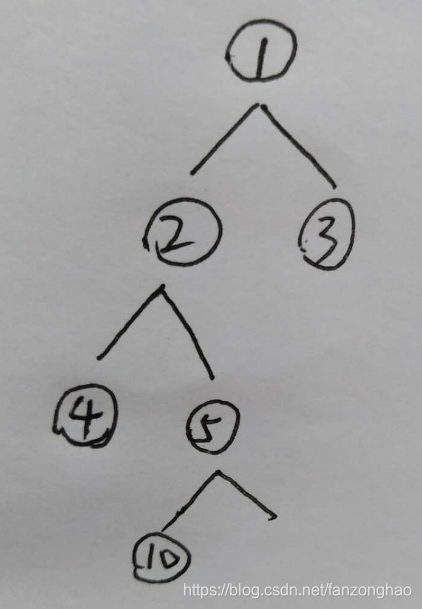
print('===root_node.left.nexts:', root_node.left.nexts)def dfs2(node):if node is None:return# nodeSet = set()stack = []print('===node.val:', node.val)# nodeSet.add(node)stack.append(node)while len(stack):cur = stack.pop()               # 弹出最近入栈的节点print('==cur.val:', cur.val)  # 打印元素值for next in cur.nexts:         # 遍历该节点的邻接节点# if next not in nodeSet:    # 如果邻接节点不重复# stack.append(cur)       # 把节点压入stack.append(next)      # 把邻接节点压入# nodeSet.add(next)  # 登记节点dfs2(root_node)

dfs压栈写法过程

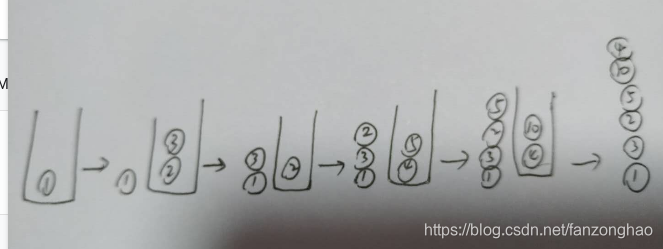
上述两种算法在搜索引擎中的应用

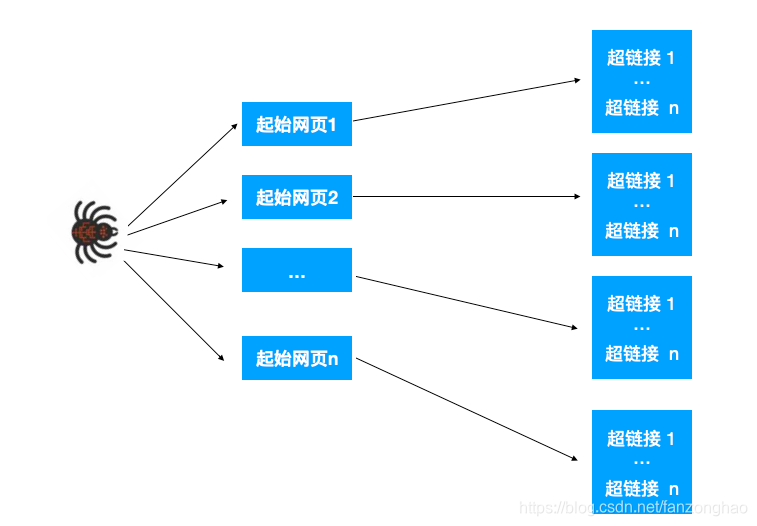
3.延展递归求图中的起始点到终止点所有路径以及最短路径

# 找到所有从start到end的路径
def findAllPath(graph, start, end, path=[]):path = path + [start]if start == end:return [path]paths = []for node in graph[start]:if node not in path:newpaths = findAllPath(graph, node, end, path)for newpath in newpaths:paths.append(newpath)return paths
# # 查找最短路径
def findShortestPath(graph, start, end, path=[]):path = path + [start]if start == end:return pathshortest_path = []for node in graph[start]:if node not in path:new_path = findShortestPath(graph, node, end, path)if len(new_path):if not len(shortest_path) or len(new_path)<len(shortest_path):shortest_path = new_pathreturn shortest_pathgraph ={'A': ['B', 'C'],'B': ['A', 'C', 'D'],'C': ['A', 'B', 'D', 'E'],'D': ['B', 'C', 'E', 'F'],'E': ['C', 'D'],'F': ['D']}allpath = findAllPath(graph, 'A', 'F')
print('\n所有路径：', allpath)shortpath = findShortestPath(graph, 'A', 'F')
print('\n最短路径：', shortpath)