一.余弦相似度

加速计算参考这篇文章

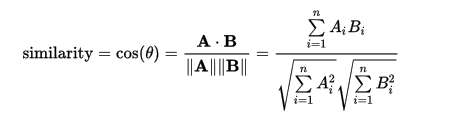
from math import *def square_rooted(x):return round(sqrt(sum([a*a for a in x])), 3)def cosine_similarity(x,y):numerator = sum(a*b for a, b in zip(x,y))denominator = square_rooted(x)*square_rooted(y)return round(numerator/float(denominator),3)res = cosine_similarity([1, 0], [0,1])
print('==res:', res)

二.欧式距离

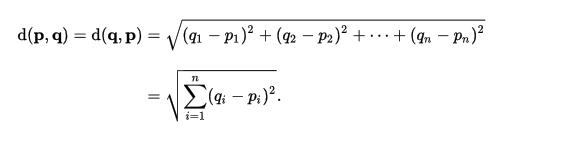
from math import *
def euclidean_distance(x, y):return sqrt(sum(pow(a - b, 2) for a, b in zip(x, y)))res = euclidean_distance([0, 1], [1, 0])
print('res:', res)

三.曼哈顿距离

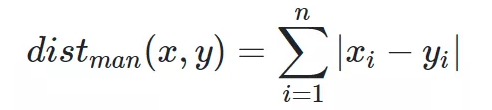
from math import *def manhattan_distance(x,y):return sum(abs(a-b) for a, b in zip(x,y))
print(manhattan_distance([1, 0], [0, 1]))

四.汉明距离

两个等长字符串在对应位置上不同字符的数目。

def hamming_distance(s1, s2):"""Return the Hamming distance between equal-length sequences"""if len(s1) != len(s2):raise ValueError("Undefined for sequences of unequal length")return sum(a != b for a, b in zip(s1, s2))res = hamming_distance('12','13')
print('res:', res)

五.切比雪夫距离

切比雪夫距离起源于国际象棋中国王的走法，国际象棋中国王每次只能往周围的8格中走一步，那么如果要从棋盘中A格(x1,y1)走到B格(x2,y2)最少需要走几步？你会发现最少步数总是max(|x2-x1|,|y2-y1|)步。有一种类似的一种距离度量方法叫切比雪夫距离。

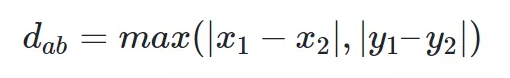
def chebyshev_distance(p, q):assert len(p) == len(q)return max([abs(x - y) for x, y in zip(p, q)])
res = chebyshev_distance([0,0], [1,3])
print('res:', res)

六.兰氏距离

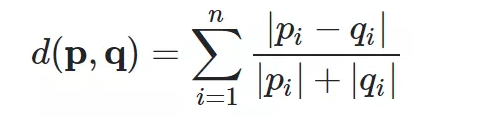
def canberra_distance(p, q):n = len(p)distance = 0for i in range(n):if p[i] == 0 and q[i] == 0:distance += 0else:distance += abs(p[i] - q[i]) / (abs(p[i]) + abs(q[i]))return distanceres = canberra_distance([1,0], [0,1])
print('res:', res)

七.闵可夫斯基距离

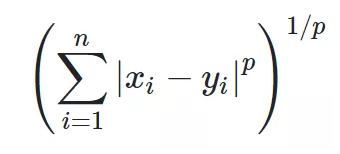
p=2即为欧氏距离，而p=1时则为曼哈顿距离。当p取无穷时的极限情况下，可以得到切比雪夫距离：

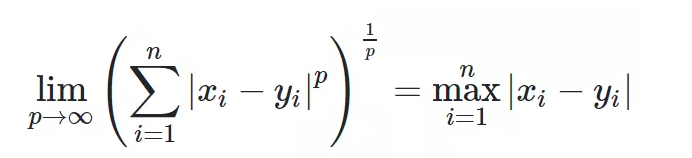
def minkowski_distance(p, q, n):assert len(p) == len(q)return sum([abs(x - y) ** n for x, y in zip(p, q)]) ** (1. / n)res = minkowski_distance([1, 0], [0, 1], n=2.)
print('res:', res)

八.编辑距离

编辑距离，又称Levenshtein距离（莱文斯坦距离也叫做Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作次数，如果它们的距离越大，说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

方法1:调包

import Levenshtein
texta = '者記聞新'
textb = '浪(第'
print(Levenshtein.distance(texta, textb))

方法2:动态规划

import os
import numpy as np
def edit_distance(S1,S2):#S1列　S2行mat = [[0] *(len(S1)+1) for i in range(len(S2)+1)]# print('mat:', mat)for i in range(len(S2)):mat[i+1][0] = mat[i][0]+1# print('mat:', mat)for i in range(len(S1)):mat[0][i+1] = mat[0][i]+1# print('mat:\n', np.array(mat))#相等就为０　不想等加１for i in range(len(S2)):for j in range(len(S1)):if S2[i] == S1[j]:# print('S2[i]:', S2[i])mat[i + 1][j + 1] = min(mat[i][j] + 0, mat[i + 1][j]+1, mat[i][j + 1]+1)else:mat[i + 1][j + 1] = min(mat[i][j] + 1, mat[i + 1][j]+1, mat[i][j + 1]+1)# print('mat:\n', np.array(mat))dis = mat[-1][-1]print('dis:', dis)return dis
# S1 = 'iva1'
# S2 = 'iva'
S2 = '者記聞新'
S1 = '浪(第'
dis = edit_distance(S1, S2)
print('dis:', dis)

九.杰卡德相似度

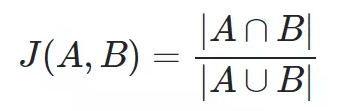
def jaccard_sim(a, b):unions = len(set(a).union(set(b)))intersections = len(set(a).intersection(set(b)))return intersections / unionsa = ['1', '0']
b = ['1', '1', '1']
res = jaccard_sim(a, b)
print('res:', res)

十.Dice距离

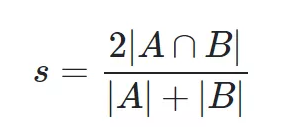
def dice_coefficient(a, b):"""dice coefficient 2nt/na + nb."""intersections = len(set(a).intersection(set(b)))return intersections * 2.0/(len(set(a)) + len(set(b)))res =  dice_coefficient(a = [1, 0], b =[0, 1])
print('===res:',res)