尺度空间

真实世界的物体只有在一定尺度上才有意义，例如我们能够看到放在桌子上的水杯，但对于整个银河系，这个水杯是不存在的。物体的这种多尺度的本质在自然界中是普遍存在的。尺度空间就是试图在数字图像领域复制这个概念。又比如，对于某幅图像，我们是想看到叶子还是想看到整棵树，如果是树，那么我们就应该有意识的去除图像的细节部分（如叶子、细枝等）。在去除细节部分的过程中，我们一定要确保不能引进新的错误的细节。因此在创建尺度空间的过程中，我们应该对原始图像逐渐的做模糊平滑处理。进行该操作的唯一方法是高斯模糊处理，因为已经被证实，高斯函数是唯一可能的尺度空间核。

（我简单的把尺度空间理解为，一副图像通过缩小后，会产生很多尺度空间，给定的一副图像我们只能进行缩小；同一个组的图像的分辨率相同，但是组内的图像依次看起来模糊，细节的部分被省略，尽大可能保留了图像的主要信息，以便于后面的特征点检测；各个组之间图像的分辨率依次减小；我们得到各类尺度空间的目的是为了检测图像中的特征点，当图像模糊、进一步缩小后，检测到的特征点可能是原图的一个区域，因此每个特征点会有半径的属性）

 

极值检测

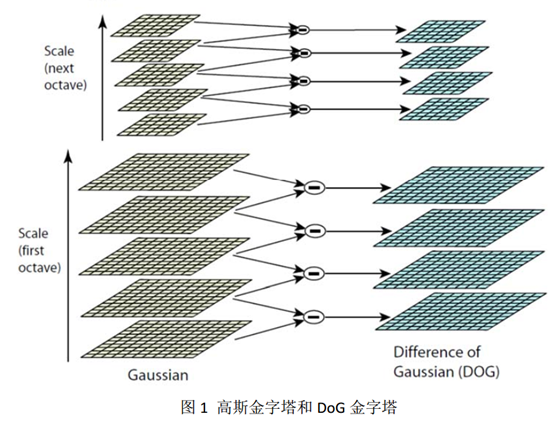
为了在连续的尺度下检测图像的特征点，需要建立 DoG 金字塔，而 DoG 金字塔的建立又离不开高斯金字塔的建立，如下图所示，左侧为高斯金字塔，右侧为 DoG 金字塔。

（下图只显示了两组尺度空间图像，两组图像的分辨率是一样的，但是每组图像里，上层图像比下层图像模糊，上面的那组图像的分辨率要小于下面的那组图像，上面的图像进行了缩小；右侧每层的尺度空间图像数目都比左侧少一个，因为左侧的每相邻的两层图像相减得到右侧的一层图像，）

 

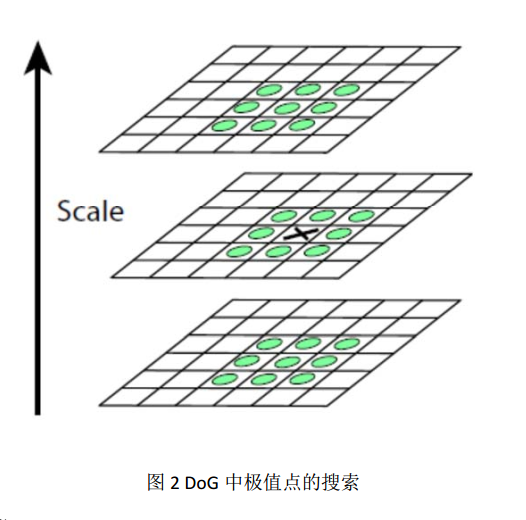
极值点的搜索是在 DoG 金字塔内进行的，这些极值点就是候选的特征点。在搜索之前，我们需要在 DoG 金字塔内剔除那些像素值过小的点，因为这些像素具有较低的对比度，它们肯定不是稳定的特征点。极值点的搜索不仅需要在它所在尺度空间图像的邻域内进行，还需要在它的相邻尺度空间图像内进行，如图 2 所示。

 

 

特征点的定位

极值点的求取是在 DoG 尺度图像内进行的， DoG 图像的一个特点就是对图像边缘有很强的响应。一旦特征点落在图像的边缘上，这些点就是不稳定的点。这是因为一方面图像边缘上的点是很难定位的，具有定位的歧义性；另一方面这样的点很容易受到噪声的干扰而变得不稳定。因此我们一定要把这些点找到并剔除掉。它的方法与 Harris 角点检测算法相似，即一个平坦的 DoG 响应峰值往往在横跨边缘的地方有较大的主曲率，而在垂直边缘的方向上有较小的主曲率。

（这一个步骤主要是去掉检测到的极值点中的图像边缘点）

 

方向角度的确定

       （确定特征点方向角度时，我们首先要确定该特征点的半径，半径和该图像的尺度有关，确定半径后，统计特征点周围各个方向半径内的像素梯度幅值和，10度为一个方向，方向统计和最大的表示该特征点的方向。）

 

特征点描述符生成

目前为止，我们已经为关键点赋予了坐标位置、尺度信息以及方向。现在我们需要一组向量将这个关键点表达出来，并且这组向量不单包括关键点，还应包括关键点周围对其有贡献的像素点。我们还期望这组向量对仿射变换、光照变换等具有一定的鲁棒性，这些不变特性将会作为目标匹配的依据。

描述子的基本思路：通过对关键点周围图像区域分块，计算块内梯度直方图，生成具有独特性的向量，这个向量是该区域图像信息的一种抽象，具有唯一性。

（特征点描述符表示这个特征点独特性的地方，区别与其他特征点的地方，找出区别主要根据特征点周围的像素值，计算特征点周围的像素值的梯度直方图，根据周围像素直方图来唯一描述特征点，通常一个特征点需要计算周围4*4个子区域，每个子区域涉及8个方向，所以每个特征点有4*4*8=128维）

 

参考自：

https://blog.csdn.net/dcrmg/article/details/52561656

http://blog.csdn.net/zhaocj/article/details/42124473

http://blog.csdn.net/liuheng0111/article/details/51234163