更多MATLAB图像处理视频请点击 http://study.163.com/course/courseMain.htm?courseId=1003594013
图像变换:
更多MATLAB图像处理视频请点击 http://study.163.com/course/courseMain.htm?courseId=1003594013
在 MATLAB 中,一般用二元函数 f(x, y) 作为图像的数学表示。 f( x, y) 表示在特定点f( x, y) 处的函数值,表示图像在该点相应的颜色强度或者灰度。所谓图像变换就是指把图像转换为另一种数学表示方式的操作。
在图像处理技术中,图像的正交变换技术有着广泛的应用,是图像处理的重要工具。通过变换图像,改变图像的表示域及表示数据,可以给后继工作带来极大的方便。例如,傅立叶变换可使处理分析在频域中进行,使运算简单;而离散余弦变换(DCT)可使能量集中在少数数据上,从而实现数据压缩,便于图像传输和存储。
1.傅立叶变换的基本概念
假设 f (m,n) 是一个包含两个离散空间变量 m 和 n 的函数,则该函数的二维傅立叶变换的定义如下:
式中, ω 1 和 ω 2 为频域变量,其单位为弧度/采样单元。通常函数 F( ω 1 , ω 2 )称为函数 f (m, n)的频域表示。F( ω 1 , ω 2 )是复变函数,其变量 ω 1 和 ω 2 的周期均为 2π。因为这种周期性的存在,所以通常在图像显示时,这两个变量的取值范围为-pi<=ω 1,ω 2<=pi.
傅立叶反变换定义如下:
简单地说,该方程说明 f (m, n)可以表示为无限多项不同频率的复指函数之和。而不同的频率点( ω 1 , ω 2 )所做的贡献由幅度 F( ω 1 , ω 2 )决定。
例如,考察下面的矩形函数 f (m, n)。该函数在一个矩形的区域中的函数值为 1,其他区域都为 0,如图 所示。
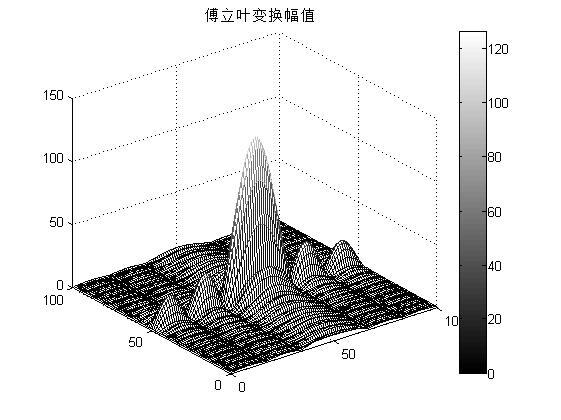
在 MATLAB 中,变量 m、n 和函数 f (m, n)均采用离散表示,所以要想真实地逼近连续函数,只能通过提高取样率。因此,f (m, n)函数的傅立叶变换可由以下程序段获得,傅立叶变换的幅值即|F( ω 1 , ω 2 )|,如图 (b)所示。其中 x 轴和 y 轴分别为水平分量和垂直分量
例:
N=100;
f=zeros(50,50);
f(15:35,23:28)=1;
figure(1);
imshow(f,'InitialMagnification','fit');title('矩形连续函数')
%图片自动适应窗口大小输出
F=fft2(f,N,N);
% F = fft2(f,N,N)是由用户设定变换区域的大小NxN。当然,如果用户设定的区域大小不是 2 的整数次方,FFT 还会有默认的补零操作
F2=fftshift(abs(F));
%fftshift的作用正是让正半轴部分和负半轴部分的图像分别关于各自的中心对称。
%因为直接用fft得出的数据与频率不是对应的,fftshift可以纠正过来
figure(2);
x=1:N;y=1:N;
mesh(x,y,F2(x,y)),title('傅立叶变换幅值');%三维网格图
colormap(gray);%输出灰色系曲面图
colorbar;%添加颜色条
2.离散傅立叶变换
在用计算机处理傅立叶变换通常采用离散傅立叶变换(Discrete Fourier Transform,DFT)。采用离散傅立叶变换主要有以下两个原因:
(1)因为 DFT 的输入/输出均为离散值,非常适用于计算机的运算操作。
(2)采用离散傅立叶变换,就可以用一种快速算法,即快速傅立叶变换(Fast FourierTransform,FFT)。
FFT 的设计思想是将原函数分为奇数项和偶数项,通过不断将一个奇数项和一个偶数项相加(减),得到需要的结果。
也就是说 FFT 是将复杂的乘法运算变成两个数相加(减)的简单运算的重复,即通过计算两个单点的 DFT,来计算两个双点的 DFT;通过计算两个双点的 DFT,来计算四个 点的DFT⋯⋯依此类推。
对于任何 N=2 m 的 DFT 的计算,通过计算两个 N/2 点的 DFT,来计算 N 个点的 DFT。
数学定义:
在 MATLAB 中,可分别用函数 fft、fft2 和 fftn 来计算一维、二维和 n 维的 FFT,而其反变换依次为 ifft、ifft2 和 ifftn。
例:
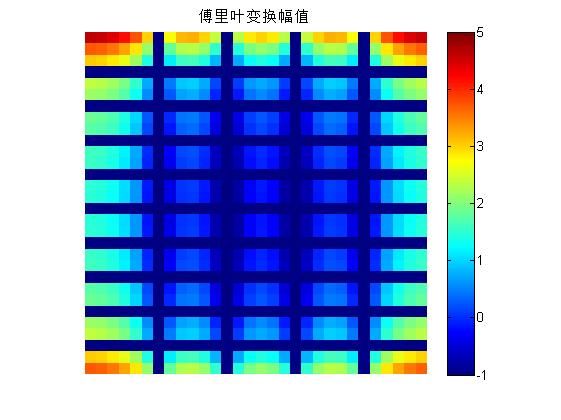
f = zeros(30,30);
f(5:24,13:17) = 1;
imshow(f,'InitialMagnification','fit');title('矩形连续函数');
%图片自动适应窗口大小输出
F = fft2(f);
F2 = log(abs(F));%输出幅度值的另一种方法
figure
imshow(F2,[-1 5],'InitialMagnification','fit'); colormap(jet); colorbar;title('傅里叶变换幅值');
%matlab colormap(jet)中数值大为红色,数值小为蓝色
在计算离散傅立叶变换时,可以通过下面的语句对被变换函数(或图像区域)进行补零操作来提高分辨率,具体调用方式如下:
F = fft2(f,M,N);M×N 表示进行补零操作后被变换区域的大小,与原区域不相重叠的区域补零。
3.利用傅立叶变换进行图像特征识别
(1)快速卷积
傅立叶变换的另一个重要特性是能够实现快速卷积。由线性系统理论可知,两个函数的卷积的傅立叶变换等于两个函数的傅立叶变换的乘积。该特性与快速傅立叶变换一
起,可以快速计算函数的卷积
fft(f1*f2)=fft(f1)x fft(f2)
f1*f2=ifft(fft(f1)xfft(f2));
(2)图像特征识别
傅立叶变换可以用于与卷积密切相关的相关运算(correlation)。在数字图像处理中的相关运算通常用于匹配模板,可以用于对某些模板对应的特征进行定位。例如,假如我们希望在图像 text.tif 中定位字母“a”,如图所示,可以采用下面的方法定位。
将包含字母“a”的图像与图像 text.png 进行相关运算,也就是对字母“a”的图像和图像 text.png 进行傅立叶变换,然后利用快速卷积的方法,计算字母“a”和图像 text.png 的卷积,提取卷积运算的峰值,即得到在图像 text.png 中对应字母“a”的定位结果。
例:
bw=imread('text.png');
>> a=bw(32:45,88:98);
>> figure,imshow(bw),title('原图,在这幅图中找出字母a的位置');
>> figure,imshow(a),title('字母a');
>>
>> C = real(ifft2(fft2(bw) .* fft2(rot90(a,2),256,256)));
figure, imshow(C,[]),title('C');
>> max(C(:))
ans =
68.0000
>> thresh=60;
>> figure,imshow(C>thresh);
>> %卷积运算的值大于60的输出为白色,小于的为黑色,卷积值反映了相似程度,越大表示越相近,当大于阈值的时候就任务是字母'a'了,
更多MATLAB图像处理视频请点击 http://study.163.com/course/courseMain.htm?courseId=1003594013
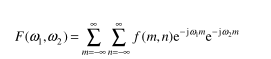
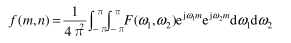

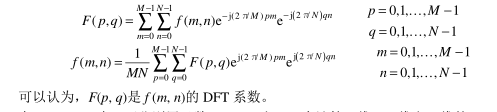





 . var in python...)
















__MessageFormat用法)
正式发布!)
